记忆化搜索
记忆化搜索
记忆化搜索(Memoization Search):是一种通过存储已经遍历过的状态信息,从而避免对同一状态重复遍历的搜索算法。
记忆化搜索是动态规划的一种实现方式。
在记忆化搜索中,当算法需要计算某个子问题的结果时,它首先检查是否已经计算过该问题。如果已经计算过,则直接返回已经存储的结果;否则,计算该问题,并将结果存储下来以备将来使用。
举个例子,比如「斐波那契数列」的定义是:𝑓(0)=0,𝑓(1)=1,𝑓(𝑛)=𝑓(𝑛−1)+𝑓(𝑛−2) 。如果我们使用递归算法求解第 𝑛 个斐波那契数,则对应的递推过程如下:
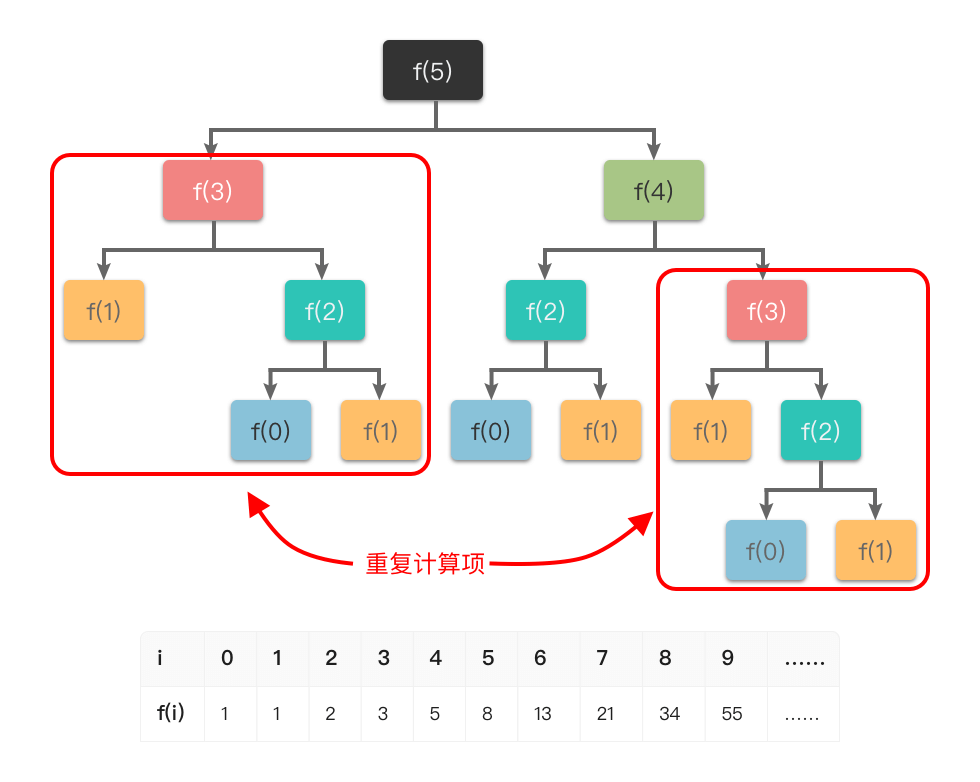
从图中可以看出:如果使用普通递归算法,想要计算 𝑓(5) ,需要先计算 f*(3) 和 f*(4),而在计算 f*(4) 时还需要计算 f*(3)。这样 𝑓(3) 就进行了多次计算,同理 f*(0)、 f*(1)、 f(2) 都进行了多次计算,从而导致了重复计算问题。
为了避免重复计算,在递归的同时,我们可以使用一个缓存(数组或哈希表)来保存已经求解过的 f*(k) 的结果。*
如上图所示,当递归调用用到 f*(*k ) 时,先查看一下之前是否已经计算过结果,如果已经计算过,则直接从缓存中取值返回,而不用再递推下去,这样就避免了重复计算问题。
使用「记忆化搜索」方法解决斐波那契数列的代码如下:
function fib(n: number): number {
// 使用数组缓存计算过的结果
const memo: number[] = new Array(n + 1).fill(null);
return myFib(n, memo);
}
function myFib(n: number, memo: number[]): number {
if (n === 0) {
return 0;
}
if (n === 1) {
return 1;
}
// 缓存中存在结果,返回结果
if (memo[n] !== null) {
return memo[n];
}
// 计算斐波那契数列
memo[n] = myFib(n - 1, memo) + myFib(n - 2, memo);
return memo[n];
}
记忆化搜索与递推区别
「记忆化搜索」与「递推」都是动态规划的实现方式,但是两者之间有一些区别。
记忆化搜索:「自顶向下」的解决问题,采用自然的递归方式编写过程,在过程中会保存每个子问题的解(通常保存在一个数组或哈希表中)来避免重复计算。
- 优点:代码清晰易懂,可以有效的处理一些复杂的状态转移方程。有些状态转移方程是非常复杂的,使用记忆化搜索可以将复杂的状态转移方程拆分成多个子问题,通过递归调用来解决。
- 缺点:可能会因为递归深度过大而导致栈溢出问题。
递推:「自底向上」的解决问题,采用循环的方式编写过程,在过程中通过保存每个子问题的解(通常保存在一个数组或哈希表中)来避免重复计算。
- 优点:避免了深度过大问题,不存在栈溢出问题。计算顺序比较明确,易于实现。
- 缺点:无法处理一些复杂的状态转移方程。有些状态转移方程非常复杂,如果使用递推方法来计算,就会导致代码实现变得非常困难。
根据记忆化搜索和递推的优缺点,我们可以在不同场景下使用这两种方法。
适合使用「记忆化搜索」的场景:
- 问题的状态转移方程比较复杂,递推关系不是很明确。
- 问题适合转换为递归形式,并且递归深度不会太深。
适合使用「递推」的场景:
- 问题的状态转移方程比较简单,递归关系比较明确。
- 问题不太适合转换为递归形式,或者递归深度过大容易导致栈溢出。
记忆化搜索解题步骤
我们在使用记忆化搜索解决问题的时候,其基本步骤如下:
- 写出问题的动态规划「状态」和「状态转移方程」。
- 定义一个缓存(数组或哈希表),用于保存子问题的解。
- 定义一个递归函数,用于解决问题。在递归函数中,首先检查缓存中是否已经存在需要计算的结果,如果存在则直接返回结果,否则进行计算,并将结果存储到缓存中,再返回结果。
- 在主函数中,调用递归函数并返回结果。
算法题
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 1137 | 第 N 个泰波那契数 | 记忆化搜索、数学、动态规划 | 简单 |
| 0494 | 目标和 | 数组、动态规划、回溯 | 中等 |
| 0375 | 猜数字大小 II | 数学、动态规划、博弈 | 中等 |
| 0576 | 出界的路径数 | 动态规划 | 中等 |
| 0087 | 扰乱字符串 | 字符串、动态规划 | 困难 |
| 0403 | 青蛙过河 | 数组、动态规划 | 困难 |
| 0552 | 学生出勤记录 II | 动态规划 | 困难 |
| 0913 | 猫和老鼠 | 图、拓扑排序、记忆化搜索、数学、动态规划、博弈 | 困难 |
| 0329 | 矩阵中的最长递增路径 | 深度优先搜索、广度优先搜索、图、拓扑排序、记忆化搜索、数组、动态规划、矩阵 | 困难 |
第 N 个泰波那契数
题目
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n,请返回第 n 个泰波那契数 Tn 的值。
示例 1:
输入:n = 4
输出:4
解释:
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4
示例 2:
输入:n = 25
输出:1389537
解法一:动态规划+记忆化搜索
根据题目递归公式,直接从 n 到 0 开始遍历,计算每一项的值,并将每一项目的值存入 map 数组中,避免重复计算。
function tribonacci(n: number): number {
// 注意: 构造数组长度为 n+1,避免边界 n 时存储数据为 undefine
let map = new Array(n + 1).fill(0)
return tribonaccis(n, map)
};
function tribonaccis(n: number, map: Array<number>): number {
if (n === 0) return 0
if (n == 1 || n == 2) return 1
// map 数组中存在值,直接返回
if (map[n] !== 0) {
return map[n]
}
//自顶向下搜索, 从 n 到 3 开始遍历,根据递推公式进行计算
for (let i = n; i >= 3; i--) {
map[i] = tribonaccis(i - 1, map) + tribonaccis(i - 2, map) + tribonaccis(i - 3, map)
// 返回计算结果
return map[i]
}
// 最终返回第n项结果
return map[n]
}
该记忆化搜索是一种「自顶向下」的解决问题,采用自然的递归方式编写过程。
解法二:动态规划+滚动数组
泰波那契数的边界条件是 T(0)=0,T(1)=1,T(2)=1 。
当 n>2 时,每一项的和都等于前三项的和,因此有如下递推关系: T(n)=T(n−1)+T(n−2)+T(n−3)
由于泰波那契数存在递推关系,因此可以使用动态规划求解。动态规划的状态转移方程即为上述递推关系,边界条件为 T(0) 、T(1) 和 T(2) 。
根据状态转移方程和边界条件,可以得到时间复杂度和空间复杂度都是 O(n) 的实现。由于 T(n) 只和前三项有关,因此可以使用「滚动数组思想」将空间复杂度优化成 O(1)。

如下的代码中给出的就是这种实现。
var tribonacci = function(n) {
if (n === 0) {
return 0;
}
if (n <= 2) {
return 1;
}
// p、q、r、s 分别是第 n-1,n-2,n-3,n 项
let p = 0, q = 0, r = 1, s = 1;
// 自底向上循环递推
for (let i = 3; i <= n; ++i) {
p = q;
q = r;
r = s;
s = p + q + r;
}
return s;
};
滚动数组是一种「自底向上」的解决问题,采用循环的方式编写过程,在过程中通过保存每个子问题的解。
目标和
题目
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
解法一:动态规划
问题分析
记数组的元素和为 sum ,添加 - 号的元素之和为 neg ,则其余添加 + 的元素之和为 sum−neg ,得到的表达式的结果为:
(sum−neg)−neg=sum−2⋅neg=targe 即: neg = (sum−target) / 2。
由于数组 nums 中的元素都是非负整数,neg 也必须是非负整数,所以上式成立的前提是 sum − target 是非负偶数。若不符合该条件可直接返回 0。
问题转换
若上式成立,问题转化成在数组 nums 中选取若干元素,使得这些元素之和等于 neg ,计算选取元素的方案数。
我们可以使用动态规划的方法求解。
动态规划求解
定义二维数组 dp ,其中 dp[i][j] 表示在数组 nums 的前 i 个数中选取元素,使得这些元素之和等于 j 的方案数。
假设数组 nums 的长度为 n ,则最终答案为 dp[n][neg]。
边界条件
当没有任何元素可以选取时,元素和只能是 0 ,对应的方案数是 1 ,因此动态规划的边界条件是:
当 1≤i≤n 时,对于数组 nums 中的第 i 个元素 num (i 的计数从 1 开始),遍历 0≤j≤neg ,计算 dp[i][j] 的值:
如果
j<num,则不能选num,此时有dp[i][j]=dp[i−1][j];如果
j≥num,则如果不选num,方案数是dp[i−1][j],如果选num,方案数是dp[i−1][j−num],此时有dp[i][j]=dp[i−1][j]+dp[i−1][j−num]。
因此状态转移方程如下:
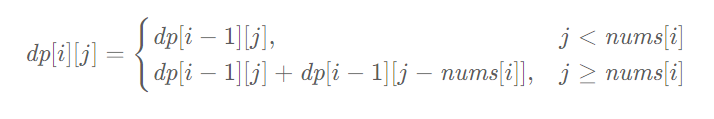
最终得到 dp[n][neg] 的值即为答案。
由此可以得到空间复杂度为 O(n×neg) 的实现。
var findTargetSumWays = function(nums, target) {
let sum = 0;
// 计算所有数和
for (const num of nums) {
sum += num;
}
// 计算总和与目标值差值
const diff = sum - target;
// 总和小于目标值,表示无法计算出目标值; 差值不为偶数,表示也无法计算出目标值
if (diff < 0 || diff % 2 !== 0) {
return 0;
}
// 计算数组长度和问题转化: dp[i][j] 表示在数组 nums 的前 i 个数中选取元素,使得这些元素之和等于 j 的方案数
const n = nums.length, neg = diff / 2;
const dp = new Array(n + 1).fill(0).map(() => new Array(neg + 1).fill(0));
dp[0][0] = 1;
for (let i = 1; i <= n; i++) {
const num = nums[i - 1];
for (let j = 0; j <= neg; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= num) {
dp[i][j] += dp[i - 1][j - num];
}
}
}
return dp[n][neg];
};
方法二:回溯
数组 nums 的每个元素都可以添加符号 + 或 - ,因此每个元素有 2 种添加符号的方法,n 个数共有 2^n 种添加符号的方法,对应 2^n 种不同的表达式。
当 n 个元素都添加符号之后,即得到一种表达式,如果表达式的结果等于目标数 target ,则该表达式即为符合要求的表达式。
可以使用回溯的方法遍历所有的表达式,回溯过程中维护一个计数器 count ,当遇到一种表达式的结果等于目标数 target 时,将 count 的值加 1。
遍历完所有的表达式之后,即可得到结果等于目标数 target 的表达式的数目。
var findTargetSumWays = function(nums, target) {
let count = 0;
const backtrack = (nums, target, index, sum) => {
if (index === nums.length) { //一次遍历完成
if (sum === target) { // 查看计算结果是否等于 target
count++;
}
} else {
// 回溯计算
backtrack(nums, target, index + 1, sum + nums[index]);
backtrack(nums, target, index + 1, sum - nums[index]);
}
}
//
backtrack(nums, target, 0, 0);
return count;
};
复杂度分析
时间复杂度:
O(2^n),其中 n 是数组 nums 的长度。回溯需要遍历所有不同的表达式,共有2^n种不同的表达式,每种表达式计算结果需要 O(1) 的时间,因此总时间复杂度是O(2^n)。空间复杂度:O(n) ,其中 n 是数组 nums 的长度。空间复杂度主要取决于递归调用的栈空间,栈的深度不超过 n 。