举个例子，如下图所示，原问题 𝑆={𝑎1,𝑎2,𝑎3,𝑎4} ，在 𝑎1 步我们通过贪心选择选出一个当前最优解之后，问题就转换为求解子问题 𝑆子问题 ={𝑎2,𝑎3,𝑎4} 。如果原问题 𝑆 的最优解可以由「第 𝑎1 步通过贪心选择的局部最优解」和「 𝑆子问题的最优解」构成，则说明该问题满足最优子结构性质。

也就是说，如果原问题的最优解包含子问题的最优解，则说明该问题满足最优子结构性质。

在做了贪心选择后，满足最优子结构性质的原问题可以分解成规模更小的类似子问题来解决，并且可以通过贪心选择和子问题的最优解推导出问题的最优解。

反之，如果不能利用子问题的最优解推导出整个问题的最优解，那么这种问题就不具有最优子结构。

贪心算法正确性的证明

贪心算法最难的部分不在于问题的求解，而在于是正确性的证明。我们常用的证明方法有「数学归纳法」和「交换论证法」。

数学归纳法：先计算出边界情况（例如 𝑛=1n=1）的最优解，然后再证明对于每个 𝑛n，𝐹𝑛+1F**n+1 都可以由 𝐹𝑛F**n 推导出。
交换论证法：从最优解出发，在保证全局最优不变的前提下，如果交换方案中任意两个元素 / 相邻的两个元素后，答案不会变得更好，则可以推定目前的解是最优解。

判断一个问题是否通过贪心算法求解，是需要进行严格的数学证明的。但是在日常写题或者算法面试中，不太会要求大家去证明贪心算法的正确性。

所以，当我们想要判断一个问题是否通过贪心算法求解时，我们可以：

凭直觉：如果感觉这道题可以通过「贪心算法」去做，就尝试找到局部最优解，再推导出全局最优解。
举反例：尝试一下，举出反例。也就是说找出一个局部最优解推不出全局最优解的例子，或者找出一个替换当前子问题的最优解，可以得到更优解的例子。如果举不出反例，大概率这道题是可以通过贪心算法求解的。

贪心算法解题步骤

转换问题：将优化问题转换为具有贪心选择性质的问题，即先做出选择，再解决剩下的一个子问题。
贪心选择性质：根据题意选择一种度量标准，制定贪心策略，选取当前状态下「最好 / 最优选择」，从而得到局部最优解。
最优子结构性质：根据上一步制定的贪心策略，将贪心选择的局部最优解和子问题的最优解合并起来，得到原问题的最优解。

应用场景

背包问题（部分版本）

给定一组物品，每种物品都有自己的重量和价值，在限定的总重量内，我们如何选择，才能使得物品的总价值最高。

活动选择问题

给定一系列活动，每个活动都有一个开始时间和结束时间，如何在给定的时间范围内选择最多的活动，使得它们之间没有重叠。

最小生成树

如Prim算法和Kruskal算法都是基于贪心策略的。

Dijkstra算法

用于计算图中单源最短路径问题。

霍夫曼编码

一种数据压缩算法，它使用变长编码表对源文件进行编码，其中变长编码表是通过对源文件中出现频率（概率估计值）进行排序构造的。

算法题

题号	标题	标签	难度
0455	分发饼干	贪心、数组、双指针、排序	简单
0860	柠檬水找零	贪心、数组	简单
0056	合并区间	数组、排序	中等
0435	无重叠区间	贪心、数组、动态规划、排序	中等
0452	用最少数量的箭引爆气球	贪心、数组、排序	中等
0055	跳跃游戏	贪心、数组、动态规划	中等
0045	跳跃游戏 II	贪心、数组、动态规划	中等
0122	买卖股票的最佳时机 II	贪心、数组	中等
0561	数组拆分	贪心、数组、计数排序、排序	简单
1710	卡车上的最大单元数	贪心、数组、排序	简单
1217	玩筹码	贪心、数组、数学	简单
1247	交换字符使得字符串相同	贪心、数学、字符串	中等
1400	构造 K 个回文字符串	贪心、哈希表、字符串、计数	中等
0921	使括号有效的最少添加	栈、贪心、字符串	中等
1029	两地调度	贪心、数组、排序	中等
1605	给定行和列的和求可行矩阵	贪心、数组、矩阵	中等
0135	分发糖果	贪心、数组	困难
0134	加油站	贪心、数组	中等
0053	最大子数组和	数组、分治、动态规划	中等
0376	摆动序列	贪心、数组、动态规划	中等
0738	单调递增的数字	贪心、数学	中等
0402	移掉 K 位数字	栈、贪心、字符串、单调栈	中等
0861	翻转矩阵后的得分	贪心、位运算、数组、矩阵	中等
0670	最大交换	贪心、数学	中等

分发饼干

题目

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

解法：枚举 + 贪心

思路

为了尽可能满足最多数量的孩子，从贪心的角度考虑，应该按照孩子的胃口从小到大的顺序依次满足每个孩子，且对于每个孩子，应该选择可以满足这个孩子的胃口且尺寸最小的饼干。

首先对数组 g 和 s 排序，然后从小到大遍历 g 中的每个元素，对于每个元素找到能满足该元素的 s 中的最小的元素。

遍历数组 g，在 s 中查找第一个大于等于 g[i] 的数组。

实现

将两个数组 g 和 s 从小到大排序；
遍历第一个数组 g，在第二个数组 s 中查找比 g[i] 或相等的首先出现数字；
计数器加1，并将 s[i] 从 s 数组中删除，并退出内层循环；

function findContentChildren(g: number[], s: number[]): number {
  let gSort = g.sort((a, b) => a - b)
  let sSort = s.sort((a, b) => a - b)
  let num = 0
  for (let i = 0; i < gSort.length; i++) {
     //遍历数组 g，在 s 中查找第一个大于等于 g[i] 的数组。
    for (let j = 0; j < sSort.length; j++) {
      if (gSort[i] <= sSort[j]) {
        num++
        sSort.splice(j, 1)
        break
      }
    }
  }
  return num
};

无重叠区间

题目

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

示例 1:

输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:

输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

解法：贪心算法

这道题我们可以转换一下思路：原题要求保证移除区间最少，使得剩下的区间互不重叠。换个角度就是：「如何使得剩下互不重叠区间的数目最多」。

那么答案就变为了：「保证移除区间最少，使得剩下的区间互不重叠」 =「总区间个数 - 不重叠区间的最多个数」。我们的问题也变成了求「所有区间中不重叠区间的最多个数」。

首先将所有区间按照它们的结束位置进行排序
然后逐个遍历排序后的区间。
在遍历过程中，我们总是选择结束位置最早的区间作为保留区间，因为这样可以为后面的区间留下更多的空间来避免重叠。
如果遇到与当前保留区间重叠的新区间，我们就将其移除（不计入最终的结果集），并继续遍历下一个区间。

我们用贪心三部曲来解决这道题。

转换问题：将原问题转变为，当选择结束值最早的区间之后，再从剩下的时间内选出最多的区间（子问题）。
贪心选择性质：每次选择时，选择结束结束值最早的区间。这样选出来的区间一定是原问题最优解的区间之一。
最优子结构性质：在上面的贪心策略下，贪心选择当前结束值最早的区间 + 剩下的区间内选出最多区间的子问题最优解，就是全局最优解。也就是说在贪心选择的方案下，能够使所有区间中不重叠区间的个数最多。

使用贪心算法的代码解决步骤描述如下：

将区间集合按照结束坐标升序排列，然后维护两个变量，一个是当前不重叠区间的结束值 𝑒𝑛𝑑_𝑝𝑜𝑠 ，另一个是不重叠区间的个数 𝑐𝑜𝑢𝑛𝑡 。初始情况下，结束坐标 𝑒𝑛𝑑_𝑝𝑜𝑠 为第一个区间的结束坐标， 𝑐𝑜𝑢𝑛𝑡为 1 。
依次遍历每段区间。对于每段区间：𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑠[𝑖]
- 如果 𝑒𝑛𝑑_𝑝𝑜𝑠 ≤ 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑠[𝑖][0] ，即 𝑒𝑛𝑑_𝑝𝑜𝑠 小于等于区间起始位置，则说明出现了不重叠区间，令不重叠区间数 𝑐𝑜𝑢𝑛𝑡 加 1 ，𝑒𝑛𝑑_𝑝𝑜𝑠更新为新区间的结束位置。
最终返回「总区间个数 - 不重叠区间的最多个数」即 𝑙𝑒𝑛(𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑠) − 𝑐𝑜𝑢𝑛𝑡 作为答案。

function eraseOverlapIntervals(intervals: number[][]): number {
  if (intervals.length === 0) {
    return 0;
  }
  // 首先，根据区间的结束位置进行排序  
  intervals.sort((a, b) => a[1] - b[1]);
  // 初始化保留的区间数为1  
  let eraseCount = 1;
  // 初始化结束位置为第一个区间的结束位置  
  let endPos = intervals[0][1]; // 记录当前已覆盖区间的结束位置  

  for (let i = 1; i < intervals.length; i++) {
    if (endPos <= intervals[i][0]) {
      // 如果当前区间的开始位置大于或等于前一个区间的结束位置，则保留当前区间  
      eraseCount++;
      endPos = intervals[i][1]; // 更新结束位置为当前区间的结束位置  
    }
  }

  // 返回需要移除的区间数，即总区间数减去保留的区间数  
  return intervals.length - eraseCount;
}

合并区间

题目

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

解法一：排序

思路

如果我们按照区间的左端点排序，那么在排完序的列表中，可以合并的区间一定是连续的。如下图所示，标记为蓝色、黄色和绿色的区间分别可以合并成一个大区间，它们在排完序的列表中是连续的：

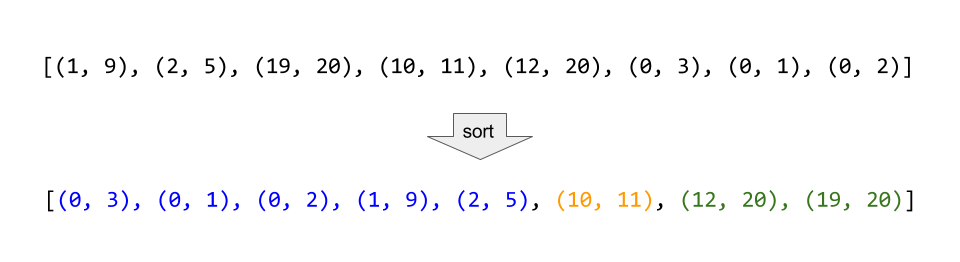
算法

我们用数组 merged 存储最终的答案。

首先，我们将列表中的区间按照左端点升序排序。
然后我们将第一个区间加入 merged 数组中，并按顺序依次考虑之后的每个区间：
- 如果当前区间的左端点在数组 merged 中最后一个区间的右端点之后，那么它们不会重合，我们可以直接将这个区间加入数组 merged 的末尾；
- 否则，它们重合，我们需要用当前区间的右端点更新数组 merged 中最后一个区间的右端点，将其置为二者的较大值。

// 定义合并区间的函数  
function merge(intervals: number[][]): number[][] {  
  // 如果传入的区间数组为空，直接返回一个空数组  
  if (intervals.length === 0) {  
    return [];  
  }  
  
  // 对区间数组进行排序，按照每个区间的起始值升序排列  
  intervals.sort((a, b) => a[0] - b[0]);  
  
  // 用于存储合并后区间的数组  
  const merged: number[][] = [];  
  
  // 遍历排序后的区间数组  
  for (let i = 0; i < intervals.length; i++) {  
    const [L, R] = intervals[i]; // 解构当前区间的起始值和结束值  
  
    // 如果合并后的数组为空，或者当前区间的起始值大于合并后数组中最后一个区间的结束值  
    // 则说明当前区间与前一个区间没有交集，直接添加到合并数组中  
    if (merged.length === 0 || merged[merged.length - 1][1] < L) {  
      merged.push([L, R]);  
    } else {  
      // 否则，当前区间与前一个区间有交集，更新前一个区间的结束值为两者结束值的较大值  
      merged[merged.length - 1][1] = Math.max(merged[merged.length - 1][1], R);  
    }  
  }  
  
  // 返回合并后的区间数组  
  return merged;  
}

加油站

题目

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则保证它是唯一的。

示例 1:

输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

解法：遍历

思路

首先计算整个环路的汽油净增量（即gas[i] - cost[i]的总和）。
- 如果总和为负，则无法完成环路，因为即使从最佳起点开始，也无法保证有足够的汽油到达下一个加油站。
在遍历过程中，我们同时检查每个加油站的汽油剩余量。
- 如果剩余量变为负，则说明无法从当前加油站到达下一个加油站，因此我们将起始加油站设为下一个加油站，并重置汽油剩余量为0。
最后，如果整个环路的汽油净增量是非负的，则说明存在某个起点可以完成环路，我们返回最后一个设置的起始加油站索引。

function canCompleteCircuit(gas: number[], cost: number[]): number {
  let totalGas = 0; // 用来记录整个环路汽油的净增量  
  let currentGas = 0; // 用来记录当前位置的汽油剩余量  
  let startIndex = 0; // 可能的起始加油站索引  
  
  for (let i = 0; i < gas.length; i++) {  
    totalGas += gas[i] - cost[i]; // 累加整个环路的汽油净增量  
    currentGas += gas[i] - cost[i]; // 累加当前位置的汽油剩余量  
  
    // 如果当前汽油剩余量小于0，则无法从当前加油站到达下一个加油站  
    // 因此我们需要重置起始加油站为下一个加油站，并重置当前汽油剩余量为0  
    if (currentGas < 0) {  
      startIndex = i + 1; // 设置为下一个加油站作为新的起始点  
      currentGas = 0; // 重置汽油剩余量  
    }  
  }  
  
  // 如果整个环路的汽油净增量小于0，则无法完成环路  
  if (totalGas < 0) {  
    return -1;  
  }  
  
  // 如果能够完成环路，则返回起始加油站的索引  
  return startIndex;  

};