线性动态规划
线性动态规划
线性动态规划:具有「线性」阶段划分的动态规划方法统称为线性动态规划(简称为「线性 DP」),如下图所示。
如果状态包含多个维度,但是每个维度上都是线性划分的阶段,也属于线性 DP。
比如背包问题、区间 DP、数位 DP 等都属于线性 DP。
线性 DP 问题的划分方法有多种方式。
- 如果按照「状态的维度数」进行分类,我们可以将线性 DP 问题分为:一维线性 DP 问题、二维线性 DP 问题,以及多维线性 DP 问题。
- 如果按照「问题的输入格式」进行分类,我们可以将线性 DP 问题分为:单串线性 DP 问题、双串线性 DP 问题、矩阵线性 DP 问题,以及无串线性 DP 问题。
本文中,我们将按照问题的输入格式进行分类,对线性 DP 问题中各种类型问题进行一一讲解
单串线性 DP 问题
单串线性规划问题是一种特殊的线性规划问题
单串线性 DP 问题:问题的输入为单个数组或单个字符串的线性 DP 问题。状态一般可定义为 𝑑𝑝[𝑖]d**p[i],表示为:
- 「以数组中第 𝑖 个位置元素 𝑛𝑢𝑚𝑠[𝑖] 为结尾的子数组(𝑛𝑢𝑚𝑠[0]...𝑛𝑢𝑚𝑠[𝑖] )」的相关解。
- 「以数组中第 𝑖−1 个位置元素 𝑛𝑢𝑚𝑠[𝑖−1] 为结尾的子数组(𝑛𝑢𝑚𝑠[0]...𝑛𝑢𝑚𝑠[𝑖−1] )」的相关解。
- 「以数组中前 𝑖 个元素为子数组(𝑛𝑢𝑚𝑠[0]...𝑛𝑢𝑚𝑠[𝑖−1] )」的相关解。
这 种状态的定义区别在于相差一个元素 𝑛𝑢𝑚𝑠[𝑖] 。
- 第 1 种状态:子数组的长度为 𝑖+1 ,子数组长度不可为空;
- 第 2 种状态、第 3 种状态:
- 这两种状态描述是相同的。子数组的长度为 𝑖 ,子数组长度可为空。
- 在 𝑖=0 ,方便用于表示空数组(以数组中前 0 个元素为子数组)。
特征
- 目标函数:存在一个目标函数,这个函数是线性的,可以表示为一组变量的线性组合。这个函数代表了在特定条件下可能达到的最优结果。
- 约束条件:问题中包含一组约束条件,这些条件也是线性的,可以表示为一组变量的线性不等式或等式。这些约束条件是在追求最优解时必须遵守的。
- 线性关系:目标函数和约束条件之间具有线性或近似线性的关系,可以用一次方程式来表示。
解题思路
对于单串线性规划问题的解题思路,通常采用单纯形法。
单纯形法是一种迭代算法,通过逐步调整决策变量的值来逼近最优解。
在每一步迭代中,算法都会根据当前的决策变量值和约束条件,计算出目标函数的新值,并判断是否已经找到最优解。
如果没有找到最优解,算法会选择一个决策变量进行调整,并继续迭代。
算法题
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 0300 | 最长递增子序列 | 数组、二分查找、动态规划 | 中等 |
| 0673 | 最长递增子序列的个数 | 树状数组、线段树、数组、动态规划 | 中等 |
| 0354 | 俄罗斯套娃信封问题 | 数组、二分查找、动态规划、排序 | 困难 |
| 0053 | 最大子数组和 | 数组、分治、动态规划 | 中等 |
| 0152 | 乘积最大子数组 | 数组、动态规划 | 中等 |
| 0918 | 环形子数组的最大和 | 队列、数组、分治、动态规划、单调队列 | 中等 |
| 0198 | 打家劫舍 | 数组、动态规划 | 中等 |
| 0213 | 打家劫舍 II | 数组、动态规划 | 中等 |
| 0740 | 删除并获得点数 | 数组、哈希表、动态规划 | 中等 |
| 1388 | 3n 块披萨 | 贪心、数组、动态规划、堆(优先队列) | 困难 |
| 0873 | 最长的斐波那契子序列的长度 | 数组、哈希表、动态规划 | 中等 |
| 1027 | 最长等差数列 | 数组、哈希表、二分查找、动态规划 | 中等 |
| 1055 | 形成字符串的最短路径 | 贪心、双指针、字符串 | 中等 |
| 0368 | 最大整除子集 | 数组、数学、动态规划、排序 | 中等 |
| 0032 | 最长有效括号 | 栈、字符串、动态规划 | 困难 |
| 0413 | 等差数列划分 | 数组、动态规划 | 中等 |
| 0091 | 解码方法 | 字符串、动态规划 | 中等 |
| 0639 | 解码方法 II | 字符串、动态规划 | 困难 |
| 0132 | 分割回文串 II | 字符串、动态规划 | 困难 |
| 1220 | 统计元音字母序列的数目 | 动态规划 | 困难 |
| 0338 | 比特位计数 | 位运算、动态规划 | 简单 |
| 0801 | 使序列递增的最小交换次数 | 数组、动态规划 | 困难 |
| 0871 | 最低加油次数 | 贪心、数组、动态规划、堆(优先队列) | 困难 |
| 0045 | 跳跃游戏 II | 贪心、数组、动态规划 | 中等 |
| 0813 | 最大平均值和的分组 | 数组、动态规划、前缀和 | 中等 |
| 0887 | 鸡蛋掉落 | 数学、二分查找、动态规划 | 困难 |
| 0256 | 粉刷房子 | 数组、动态规划 | 中等 |
| 0265 | 粉刷房子 II | 数组、动态规划 | 困难 |
| 1473 | 粉刷房子 III | 数组、动态规划 | 困难 |
| 0975 | 奇偶跳 | 栈、数组、动态规划、有序集合、单调栈 | 困难 |
| 0403 | 青蛙过河 | 数组、动态规划 | 困难 |
| 1478 | 安排邮筒 | 数组、数学、动态规划、排序 | 困难 |
| 1230 | 抛掷硬币 | 数学、动态规划、概率与统计 | 中等 |
| 0410 | 分割数组的最大值 | 贪心、数组、二分查找、动态规划、前缀和 | 困难 |
| 1751 | 最多可以参加的会议数目 II | 数组、二分查找、动态规划、排序 | 困难 |
| 1787 | 使所有区间的异或结果为零 | 位运算、数组、动态规划 | 困难 |
| 0121 | 买卖股票的最佳时机 | 数组、动态规划 | 简单 |
| 0122 | 买卖股票的最佳时机 II | 贪心、数组 | 中等 |
| 0123 | 买卖股票的最佳时机 III | 数组、动态规划 | 困难 |
| 0188 | 买卖股票的最佳时机 IV | 数组、动态规划 | 困难 |
| 0309 | 最佳买卖股票时机含冷冻期 | 数组、动态规划 | 中等 |
| 0714 | 买卖股票的最佳时机含手续费 | 贪心、数组 | 中等 |
最长递增子序列
题目
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
解法:动态规划
1. 划分阶段
按照子序列的结尾位置进行阶段划分。
2. 定义状态
定义状态 𝑑𝑝[𝑖] 表示为:以 𝑛𝑢𝑚𝑠[𝑖] 结尾的最长递增子序列长度。
3. 状态转移方程
一个较小的数后边如果出现一个较大的数,则会形成一个更长的递增子序列。
对于满足 0≤𝑗<𝑖 的数组元素 𝑛𝑢𝑚𝑠[𝑗] 和 𝑛𝑢𝑚𝑠[𝑖] 来说:
- 如果
𝑛𝑢𝑚𝑠[𝑗]<𝑛𝑢𝑚𝑠[𝑖],则𝑛𝑢𝑚𝑠[𝑖]可以接在𝑛𝑢𝑚𝑠[𝑗]后面,此时以𝑛𝑢𝑚𝑠[𝑖]结尾的最长递增子序列长度会在「以𝑛𝑢𝑚𝑠[𝑗]结尾的最长递增子序列长度」的基础上加 1 ,即:𝑑𝑝[𝑖]=𝑑𝑝[𝑗]+1。 - 如果
𝑛𝑢𝑚𝑠[𝑗]>=𝑛𝑢𝑚𝑠[𝑖],则𝑛𝑢𝑚𝑠[𝑖]不可以接在𝑛𝑢𝑚𝑠[𝑗]后面,可以直接跳过。
综上,我们的状态转移方程为:𝑑𝑝[𝑖]=𝑚𝑎𝑥(𝑑𝑝[𝑖],𝑑𝑝[𝑗]+1), 0≤𝑗<𝑖。
4. 初始条件
默认状态下,把数组中的每个元素都作为长度为 1 的递增子序列。即 𝑑𝑝[𝑖]=1 。
5. 最终结果
根据我们之前定义的状态,𝑑𝑝[𝑖] 表示为:以 𝑛𝑢𝑚𝑠[𝑖] 结尾的最长递增子序列长度。那为了计算出最大的最长递增子序列长度,则需要再遍历一遍 𝑑𝑝 数组,求出最大值即为最终结果。
function lengthOfLIS(nums: number[]): number {
const size = nums.length;
const dp = new Array(size).fill(1);
// 遍历数组,查找 以 𝑛𝑢𝑚𝑠[𝑖] 结尾的最长递增子序列长度
for (let i = 0; i < size; i++) {
for (let j = 0; j < i; j++) {
// 𝑛𝑢𝑚𝑠[𝑖] 可以接在 𝑛𝑢𝑚𝑠[𝑗] 后面
if (nums[j] < nums[i] ) {
//此时以 𝑛𝑢𝑚𝑠[𝑖] 结尾的最长递增子序列长度会在「以𝑛𝑢𝑚𝑠[𝑗] 结尾的最长递增子序列长度」的基础上加 1 ,即:𝑑𝑝[𝑖]=𝑑𝑝[𝑗]+1
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
return Math.max(...dp);
}
复杂度分析
- 时间复杂度:
𝑂(𝑛^2)。两重循环遍历的时间复杂度是𝑂(𝑛^2),最后求最大值的时间复杂度是 𝑂(𝑛) ,所以总体时间复杂度为𝑂(𝑛^2)。 - 空间复杂度:𝑂(𝑛) 。用到了一维数组保存状态,所以总体空间复杂度为 𝑂(𝑛)
HJ24 合唱队
解法:动态规划
分析题目可得,题目实际求最长递增子序列的变种题目,加了一个约束条件:需要左边递增右边递减的情况。
- 先找到每一个位置i左侧的最长上升子序列长度left[i] ;
- 再找到每一个位置i右侧的最长下降子序列长度right[i] ;
- 求出 所有位置的最长序列长度=左侧最长子序列长度+右侧最长子序列长度-1(因为同一个位置被算了两次,所以减1)
- 需要出队的人数=总人数-最长序列长度
// 处理输入数组的函数
function dp(arr: number[]) {
const n = arr.length;
const left: number[] = new Array(n).fill(1); // 存储每个数左边小于其的数的个数
const right: number[] = new Array(n).fill(1); // 存储每个数右边小于其的数的个数
// 计算每个位置左侧的最长递增
for (let i = 1; i < n; i++) {
for (let j = 0; j < i; j++) {
if (arr[i] > arr[j]) {
left[i] = Math.max(left[j] + 1, left[i]);
}
}
}
// 计算每个位置右侧的最长递减
for (let i = n - 2; i >= 0; i--) {
for (let j = n - 1; j > i; j--) {
if (arr[i] > arr[j]) {
right[i] = Math.max(right[j] + 1, right[i]);
}
}
}
// 记录每个位置的值
const result: number[] = new Array(n);
for (let i = 0; i < n; i++) {
result[i] = left[i] + right[i] - 1; // 两个都包含本身
}
// 找到最大的满足要求的值
let max = 1;
for (let i = 0; i < n; i++) {
max = Math.max(result[i], max);
}
console.log(n - max);
}
双串线性 DP 问题
双串线性动态规划问题涉及两个字符串,通常需要考虑两个字符串之间的某种关系或交互。这类问题的一个关键特征是,在解决子问题时,需要考虑两个字符串中的不同位置,通常使用两个变量(如i和j)来分别表示两个字符串中的当前位置。
在双串线性动态规划问题中,通常会定义一个二维数组dp[i][j],其中dp[i][j]表示在考虑第一个字符串的前i个字符和第二个字符串的前 j 个字符时,原问题的解。
因此,dp[i][j]的值通常与dp[i-1][j]、dp[i][j-1]和dp[i-1][j-1]等更小的子问题的解有关。
双串线性 DP 问题:问题的输入为两个数组或两个字符串的线性 DP 问题。状态一般可定义为
𝑑𝑝[𝑖][𝑗],表示为:
- 「以第一个数组中第
𝑖个位置元素𝑛𝑢𝑚𝑠1[𝑖]为结尾的子数组(𝑛𝑢𝑚𝑠1[0]...𝑛𝑢𝑚𝑠1[𝑖])」与「以第二个数组中第𝑗个位置元素𝑛𝑢𝑚𝑠2[𝑗]为结尾的子数组(𝑛𝑢𝑚𝑠2[0]...𝑛𝑢𝑚𝑠2[𝑗])」的相关解。- 「以第一个数组中第
𝑖−1个位置元素𝑛𝑢𝑚𝑠1[𝑖−1]为结尾的子数组(𝑛𝑢𝑚𝑠1[0]...𝑛𝑢𝑚𝑠1[𝑖−1])」与「以第二个数组中第𝑗−1个位置元素𝑛𝑢𝑚𝑠2[𝑗−1]为结尾的子数组(𝑛𝑢𝑚𝑠2[0]...𝑛𝑢𝑚𝑠2[𝑗−1])」的相关解。- 「以第一个数组中前
𝑖个元素为子数组(𝑛𝑢𝑚𝑠1[0]...𝑛𝑢𝑚𝑠1[𝑖−1])」与「以第二个数组中前𝑗个元素为子数组(𝑛𝑢𝑚𝑠2[0]...𝑛𝑢𝑚𝑠2[𝑗−1])」的相关解。
这 3 种状态的定义区别在于相差一个元素 𝑛𝑢𝑚𝑠1[𝑖] 或 𝑛𝑢𝑚𝑠2[𝑗] 。
- 第 1 种状态:子数组的长度为
𝑖+1或𝑗+1,子数组长度不可为空; - 第 2 种状态、第 3 种状态:子数组的长度为 𝑖 或 𝑗 ,子数组长度可为空。𝑖=0 或 𝑗=0 时,方便用于表示空数组(以数组中前 0 个元素为子数组)。
算法题
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 1143 | 最长公共子序列 | 字符串、动态规划 | 中等 |
| 0712 | 两个字符串的最小ASCII删除和 | 字符串、动态规划 | 中等 |
| 0718 | 最长重复子数组 | 数组、二分查找、动态规划、滑动窗口、哈希函数、滚动哈希 | 中等 |
| 0583 | 两个字符串的删除操作 | 字符串、动态规划 | 中等 |
| 0072 | 编辑距离 | 字符串、动态规划 | 困难 |
| 0044 | 通配符匹配 | 贪心、递归、字符串、动态规划 | 困难 |
| 0010 | 正则表达式匹配 | 递归、字符串、动态规划 | 困难 |
| 0097 | 交错字符串 | 字符串、动态规划 | 中等 |
| 0115 | 不同的子序列 | 字符串、动态规划 | 困难 |
| 0087 | 扰乱字符串 | 字符串、动态规划 | 困难 |
最长公共子序列
题目
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。
解法:动态规划
1. 划分阶段
按照两个字符串的结尾位置进行阶段划分。
2. 定义状态
定义状态 𝑑𝑝[𝑖][𝑗] 表示为:「以 𝑡𝑒𝑥𝑡1 中前 𝑖 个元素组成的子字符串 𝑠𝑡𝑟1 」与「以 𝑡𝑒𝑥𝑡2 中前 𝑗 个元素组成的子字符串 𝑠𝑡𝑟2 」的最长公共子序列长度为 𝑑𝑝[𝑖][𝑗] 。
3. 状态转移方程
双重循环遍历字符串 𝑡𝑒𝑥𝑡1 和 𝑡𝑒𝑥𝑡2 ,则状态转移方程为:
如果
𝑡𝑒𝑥𝑡1[𝑖−1] = 𝑡𝑒𝑥𝑡2[𝑗−1],说明两个子字符串的最后一位是相同的,所以最长公共子序列长度加 1 。即:
𝑑𝑝[𝑖][𝑗] = 𝑑𝑝[𝑖−1][𝑗−1] + 1。如果
𝑡𝑒𝑥𝑡1[𝑖−1] ≠ 𝑡𝑒𝑥𝑡2[𝑗−1],说明两个子字符串的最后一位是不同的,则𝑑𝑝[𝑖][𝑗]需要考虑以下两种情况,取两种情况中最大的那种:𝑑𝑝[𝑖][𝑗] = 𝑚𝑎𝑥( 𝑑𝑝[𝑖−1][𝑗], 𝑑𝑝[𝑖][𝑗−1] )。- 「以
𝑡𝑒𝑥𝑡1中前𝑖−1个元素组成的子字符串𝑠𝑡𝑟1」与「以𝑡𝑒𝑥𝑡2中前 𝑗 个元素组成的子字符串𝑠𝑡𝑟2」的最长公共子序列长度,即𝑑𝑝[𝑖−1][𝑗]。 - 「以
𝑡𝑒𝑥𝑡1中前 𝑖 个元素组成的子字符串𝑠𝑡𝑟1」与「以𝑡𝑒𝑥𝑡2中前 𝑗−1 个元素组成的子字符串 𝑠𝑡𝑟2 」的最长公共子序列长度,即𝑑𝑝[𝑖][𝑗−1]。
- 「以
4. 初始条件
- 当 𝑖=0 时,𝑠𝑡𝑟1 表示的是空串,空串与 𝑠𝑡𝑟2 的最长公共子序列长度为 0 ,即
𝑑𝑝[0][𝑗]=0。 - 当 𝑗=0 时,𝑠𝑡𝑟2 表示的是空串,𝑠𝑡𝑟1 与 空串的最长公共子序列长度为 0 ,即
𝑑𝑝[𝑖][0]=0。
5. 最终结果
根据状态定义,最后输出 𝑑𝑝[𝑠𝑖𝑠𝑒1][𝑠𝑖𝑧𝑒2] (即 𝑡𝑒𝑥𝑡1 与 𝑡𝑒𝑥𝑡2 的最长公共子序列长度)即可,其中 𝑠𝑖𝑧𝑒1 、𝑠𝑖𝑧𝑒2 分别为 𝑡𝑒𝑥𝑡1 、𝑡𝑒𝑥𝑡2 的字符串长度。
// 最长公共子序列函数
longestCommonSubsequence(text1: string, text2: string): number {
// 获取两个字符串的长度
const size1 = text1.length;
const size2 = text2.length;
// 创建一个二维数组dp来存储最长公共子序列的长度
// 注意:由于索引从0开始,而我们需要考虑空字符串的情况,所以数组的大小要比字符串长度大1
const dp: number[][] = Array.from({ length: size1 + 1 }, () => Array(size2 + 1).fill(0));
// 遍历两个字符串的所有字符
for (let i = 1; i <= size1; i++) {
for (let j = 1; j <= size2; j++) {
// 如果当前字符相等,则最长公共子序列长度等于去掉这两个字符后的子串的最长公共子序列长度加1
if (text1[i - 1] === text2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
// 如果当前字符不相等,则最长公共子序列长度等于两个方向上的最长公共子序列长度的较大值
// 一个方向是去掉text1的当前字符,另一个方向是去掉text2的当前字符
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// 返回整个字符串的最长公共子序列长度
return dp[size1][size2];
}
矩阵线性 DP问题
矩阵线性动态规划问题,也称为坐标类动态规划问题
通常涉及一个给定的矩阵,矩阵中包含一些信息,求解者需要根据这些信息来求解问题。
特征
这类问题的一个主要特征是将整个矩阵视为一个图,矩阵中的每个位置上的元素看作是图上的节点,而每个节点的邻居则是其相邻的上下左右的位置。
解题思路
在解决这类问题时,一般的解题思路是遍历矩阵(即遍历图),在遍历的过程中记录一些临时的状态,这些状态实际上就是子问题的答案。通过记录并推导这些子问题的答案,最终可以得到我们想要的答案。
具体来说,思考当前位置的状态,并尝试观察当前位置与其邻居之间的递进关系,从而得出递推方程。
递推方程描述了如何从较小的子问题(即较小规模的矩阵部分)的解推导出较大问题的解。
通过不断地应用递推方程,可以从矩阵的左上角(或右下角,取决于问题的具体定义)开始,逐步推导出整个矩阵的答案。
矩阵线性 DP 问题:问题的输入为二维矩阵的线性 DP 问题。状态一般可定义为
𝑑𝑝[𝑖][𝑗],表示为:从「位置 (0,0) 」到达「位置 (𝑖,𝑗) 」的相关解。
算法题
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 0118 | 杨辉三角 | 数组、动态规划 | 简单 |
| 0119 | 杨辉三角 II | 数组、动态规划 | 简单 |
| 0120 | 三角形最小路径和 | 数组、动态规划 | 中等 |
| 0064 | 最小路径和 | 数组、动态规划、矩阵 | 中等 |
| 0174 | 地下城游戏 | 数组、动态规划、矩阵 | 困难 |
| 0221 | 最大正方形 | 数组、动态规划、矩阵 | 中等 |
| 0931 | 下降路径最小和 | 数组、动态规划、矩阵 | 中等 |
| 0576 | 出界的路径数 | 动态规划 | 中等 |
| 0085 | 最大矩形 | 栈、数组、动态规划、矩阵、单调栈 | 困难 |
| 0363 | 矩形区域不超过 K 的最大数值和 | 数组、二分查找、矩阵、有序集合、前缀和 | 困难 |
| 面试题 17.24 | 最大子矩阵 | 数组、动态规划、矩阵、前缀和 | 困难 |
| 1444 | 切披萨的方案数 | 记忆化搜索、数组、动态规划、矩阵 | 困难 |
最大正方形
题目
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:
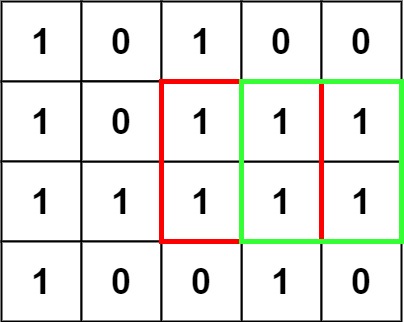
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
示例 2:
输入:matrix = [["0","1"],["1","0"]]
输出:1
示例 3:
输入:matrix = [["0"]]
输出:0
解法:动态规划
1. 划分阶段
按照正方形的右下角坐标进行阶段划分。
2. 定义状态
定义状态 𝑑𝑝[𝑖][𝑗] 表示为:以矩阵位置 (𝑖,𝑗) 为右下角,且值包含 1 的正方形的最大边长。
3. 状态转移方程
只有当矩阵位置 (𝑖,𝑗) 值为 1 时,才有可能存在正方形。
- 如果矩阵位置
(𝑖,𝑗)上值为 0,则𝑑𝑝[𝑖][𝑗] = 0。 - 如果矩阵位置
(𝑖,𝑗)上值为 1 ,则𝑑𝑝[𝑖][𝑗]的值由该位置上方矩形、左侧矩形、左上方矩形三者共同约束的,为三者中面积最小值加 1。即:𝑑𝑝[𝑖][𝑗]=𝑚𝑖𝑛(𝑑𝑝[𝑖−1][𝑗−1],𝑑𝑝[𝑖−1][𝑗],𝑑𝑝[𝑖][𝑗−1])+1。
4. 初始条件
- 默认所有以矩阵位置
(𝑖,𝑗)为右下角,且值包含 1 的正方形的最大边长都为 0 ,即𝑑𝑝[𝑖][𝑗]=0。
5. 最终结果
根据我们之前定义的状态, 𝑑𝑝[𝑖][𝑗] 表示为:以矩阵位置 (𝑖,𝑗) 为右下角,且值包含 1 的正方形的最大边长。则最终结果为所有 𝑑𝑝[𝑖][𝑗] 中的最大值。
function maximalSquare(matrix: string[][]): number {
// 检查输入矩阵是否为空
if (matrix.length === 0 || matrix[0].length === 0) {
return 0;
}
// 获取矩阵的行数和列数
const rows = matrix.length;
const cols = matrix[0].length;
// 初始化动态规划数组,比原始矩阵多一行一列以简化边界条件
const dp: number[][] = Array.from({ length: rows + 1 }, () => Array(cols + 1).fill(0));
let max_size = 0; // 用于存储最大正方形的边长
// 遍历矩阵中的每个元素,因为起始多设置一行和一列,因此 i,j 从 1 开始
for (let i = 1; i <= rows; i++) {
for (let j = 1; j <= cols; j++) {
// 如果当前元素为'1'
if (matrix[i - 1][j - 1] === '1') {
// 如果当前元素是第一行或第一列的元素,则其正方形边长只能是1
if (i === 1 || j === 1) {
dp[i][j] = 1;
} else {
// 否则,计算当前位置的正方形边长
// 取上方、左方和左上方的最小值,然后加1
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1;
}
// 更新最大正方形的边长
max_size = Math.max(max_size, dp[i][j]);
}
}
}
// 返回最大正方形的面积(边长乘以边长)
return max_size * max_size;
}
// 示例
const matrix = [
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
];
console.log(maximalSquare(matrix)); // 输出应为 4,因为存在一个2x2的正方形
复杂度分析
- 时间复杂度:
𝑂(𝑚×𝑛),其中 𝑚 、𝑛 分别为二维矩阵𝑚𝑎𝑡𝑟𝑖𝑥的行数和列数。 - 空间复杂度:
𝑂(𝑚×𝑛)
无串线性 DP 问题
无串线性 DP 问题:指那些不涉及字符串操作,且状态转移具有线性关系的动态规划问题。
算法题
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 1137 | 第 N 个泰波那契数 | 记忆化搜索、数学、动态规划 | 简单 |
| 0650 | 只有两个键的键盘 | 数学、动态规划 | 中等 |
| 0264 | 丑数 II | 哈希表、数学、动态规划、堆(优先队列) | 中等 |
| 0279 | 完全平方数 | 广度优先搜索、数学、动态规划 | 中等 |
| 0343 | 整数拆分 | 数学、动态规划 | 中等 |
整数拆分
题目
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
解法:动态规划
1. 划分阶段
按照正整数进行划分。
2. 定义状态
定义状态 𝑑𝑝[𝑖] 表示为:将正整数 𝑖 拆分为至少 2 个正整数的和之后,这些正整数的最大乘积。
3. 状态转移方程
当 𝑖≥2 时,假设正整数 𝑖 拆分出的第 1 个正整数是 𝑗 (1≤𝑗<𝑖) ,则有两种方法:
𝑖−𝑗不能拆分:将𝑖拆分为𝑗和𝑖−𝑗的和,且𝑖−𝑗不能再拆分为多个正整数,此时乘积为:𝑗×(𝑖−𝑗)。𝑖−𝑗继续拆分:将𝑖拆分为𝑗和𝑖−𝑗的和,且𝑖−𝑗继续拆分为多个正整数,此时乘积为:𝑗×𝑑𝑝[𝑖−𝑗]。
则 𝑑𝑝[𝑖] 取两者中的最大值。即:𝑑𝑝[𝑖] = 𝑚𝑎𝑥( 𝑗×(𝑖−𝑗) , 𝑗×𝑑𝑝[𝑖−𝑗]) )。
由于 1≤𝑗<𝑖 ,需要遍历 𝑗 得到 𝑑𝑝[𝑖] 的最大值,则状态转移方程如下:
𝑑𝑝[𝑖] = 𝑚𝑎𝑥{ 𝑚𝑎𝑥( 𝑗×(𝑖−𝑗) , 𝑗×𝑑𝑝[𝑖−𝑗] ) } (1≤𝑗<𝑖)。
4. 初始条件
- 0 和 1 都不能被拆分,所以
𝑑𝑝[0]=0,𝑑𝑝[1]=0。
5. 最终结果
根据我们之前定义的状态,𝑑𝑝[𝑖] 表示为:将正整数 𝑖 拆分为至少 2 个正整数的和之后,这些正整数的最大乘积。则最终结果为 𝑑𝑝[𝑛] 。
integerBreak(n: number): number {
// 创建一个长度为 n+1 的数组来保存子问题的解,dp[i] 表示数字 i 可以被分解为的最大乘积
const dp: number[] = new Array(n + 1).fill(0);
// 初始化 dp[1] 为 1,因为单个数字的最大乘积就是它本身
dp[1] = 1;
// 遍历从 2 到 n 的所有数字
for (let i = 2; i <= n; i++) {
// 遍历从 1 到 i-1 的所有可能的因子 j
for (let j = 1; j < i; j++) {
// 对于每个因子 j,计算将 i 分解为 j 和 (i-j) 的乘积
// 同时考虑 j 和 (i-j) 是否可以进一步分解为更大的乘积(即使用 dp 数组)
// 更新 dp[i] 为这两个值中的较大者
dp[i] = Math.max(dp[i], Math.max(j * (i - j), dp[j] * (i - j)));
}
}
// 返回 dp[n],即数字 n 可以被分解为的最大乘积
return dp[n];
}
复杂度分析
- 时间复杂度:𝑂(𝑛2) 。
- 空间复杂度:𝑂(𝑛) 。