背包问题
背包问题
背包问题的定义
背包问题:背包问题是线性 DP 问题中一类经典而又特殊的模型。背包问题可以描述为:给定一组物品,每种物品都有自己的重量、价格以及数量。再给定一个最多能装重量为 𝑊 的背包。现在选择将一些物品放入背包中,请问在总重量不超过背包载重上限的情况下,能装入背包的最大价值总和是多少?

根据物品限制条件的不同,背包问题可分为:
- 0-1 背包问题
- 完全背包问题
- 多重背包问题
- 分组背包问题
- 混合背包问题
背包问题的暴力解题思路
假设有 𝑛 件物品:
- 枚举出这 𝑛 件物品所有可能的组合。
- 然后再判断这些组合中的物品是否能放入背包,以及是否能得到最大价值。
这种做法的时间复杂度是 𝑂(2^𝑛) 。
背包问题暴力解法的时间复杂度是指数级别的,我们可以利用动态规划算法减少一下时间复杂度。
interface Item {
weight: number; // 物品重量
price: number; // 物品价格
quantity: number; // 物品数量
}
function knapsackBruteForce(items: Item[], W: number): number {
let maxPrice = 0; // 最大价值
// 定义一个辅助函数来递归地尝试所有可能的组合
function tryCombinations(index: number, currentWeight: number, currentPrice: number): void {
// 如果当前重量超过背包载重或已经处理完所有物品,返回
if (currentWeight > W || index >= items.length) {
return;
}
// 不选择当前物品,继续处理下一个物品
tryCombinations(index + 1, currentWeight, currentPrice);
// 尝试选择当前物品(如果还有剩余且不会超过背包载重)
const maxToAdd = Math.min(items[index].quantity, Math.floor((W - currentWeight) / items[index].weight));
for (let i = 1; i <= maxToAdd; i++) {
const newWeight = currentWeight + i * items[index].weight;
const newPrice = currentPrice + i * items[index].price;
// 更新最大价值
if (newPrice > maxPrice && newWeight <= W) {
maxPrice = newPrice;
}
// 递归地尝试其他组合
tryCombinations(index + 1, newWeight, newPrice);
}
}
// 从第一个物品开始尝试所有组合
tryCombinations(0, 0, 0);
return maxPrice;
}
// 示例使用
const items: Item[] = [
{ weight: 10, price: 60, quantity: 2 },
{ weight: 20, price: 100, quantity: 1 },
{ weight: 30, price: 120, quantity: 1 },
];
const W = 50;
console.log(knapsackBruteForce(items, W)); // 输出最大价值
0-1 背包问题基本思路
0-1 背包问题的特点:每种物品有且仅有 1 件,可以选择不放入背包,也可以选择放入背包。
思路 1:动态规划 + 二维基本思路
1. 划分阶段
按照物品的序号、当前背包的载重上限进行阶段划分。
2. 定义状态
定义状态 𝑑𝑝[𝑖][𝑤] 表示为:前 𝑖 件物品放入一个最多能装重量为 𝑤 的背包中,可以获得的最大价值。
状态 𝑑𝑝[𝑖][𝑤] 是一个二维数组,其中第一维代表「当前正在考虑的物品」,第二维表示「当前背包的载重上限」,二维数组值表示「可以获得的最大价值」。
3. 状态转移方程
对于「将前 𝑖 件物品放入一个最多能装重量为 𝑤 的背包中,可以获得的最大价值 」这个子问题,如果我们只考虑第 𝑖−1 件物品(前 𝑖 件物品中最后一件物品)的放入策略(放入背包和不放入背包两种策略)。
则问题可以转换为一个只跟前 𝑖−1 件物品相关的问题:
- 第 𝑖−1 件物品不放入背包:问题转换为「
前 𝑖−1 件物品放入一个最多能装重量为 𝑤 的背包中 ,可以获得的最大价值」为𝑑𝑝[𝑖−1][𝑤]。 - 第 𝑖−1 件物品放入背包:问题转换为「
前 𝑖−1 件物品放入一个最多能装重量为 𝑤−𝑤𝑒𝑖𝑔ℎ𝑡[𝑖−1] 的背包中,可以获得的最大价值」为𝑑𝑝[𝑖−1][𝑤−𝑤𝑒𝑖𝑔ℎ𝑡[𝑖−1]],再加上「放入的第 𝑖−1 件物品的价值」为𝑣𝑎𝑙𝑢𝑒[𝑖−1],则此时可以获得的最大价值为𝑑𝑝[𝑖−1][𝑤−𝑤𝑒𝑖𝑔ℎ𝑡[𝑖−1]] + 𝑣𝑎𝑙𝑢𝑒[𝑖−1]。
接下来我们再来考虑一下第 𝑖−1 件物品满足什么条件时才能考虑是否放入背包,并且在什么条件下一定不能放入背包:
- 如果当前背包的载重不足时(即
𝑤<𝑤𝑒𝑖𝑔ℎ𝑡[𝑖−1]):第 𝑖−1 件物品一定不能放入背包,此时背包的价值𝑑𝑝[𝑖][𝑤]仍为𝑑𝑝[𝑖−1][𝑤]时的价值,即𝑑𝑝[𝑖][𝑤]=𝑑𝑝[𝑖−1][𝑤]。 - 如果当前背包的载重足够时(即
𝑤≥𝑤𝑒𝑖𝑔ℎ𝑡[𝑖−1]):第 𝑖−1 件物品可以考虑放入背包,或者不放入背包,此时背包的价值取两种情况下的最大值,即𝑑𝑝[𝑖][𝑤]=𝑚𝑎𝑥{𝑑𝑝[𝑖−1][𝑤],𝑑𝑝[𝑖−1][𝑤−𝑤𝑒𝑖𝑔ℎ𝑡[𝑖−1]]+𝑣𝑎𝑙𝑢𝑒[𝑖−1]}。
则状态转移方程为:
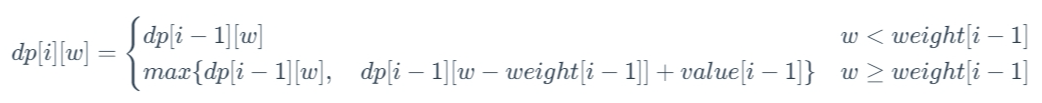
4. 初始条件
- 如果背包载重上限为 0 ,则无论选取什么物品,可以获得的最大价值一定是 0 ,即
𝑑𝑝[𝑖][0]=0,0≤𝑖≤𝑠𝑖𝑧𝑒。 - 无论背包载重上限是多少,前 0 件物品所能获得的最大价值一定为 0,即
𝑑𝑝[0][𝑤]=0,0≤𝑤≤𝑊。
5. 最终结果
根据我们之前定义的状态,𝑑𝑝[𝑖][𝑤] 表示为:前 𝑖 件物品放入一个最多能装重量为 𝑤 的背包中,可以获得的最大价值。则最终结果为 𝑑𝑝[𝑠𝑖𝑧𝑒][𝑊] ,其中 𝑠𝑖𝑧𝑒 为物品的件数,𝑊 为背包的载重上限。
// 思路 1:动态规划 + 二维基本思路
zeroOnePackMethod1(weight: number[], value: number[], W: number): number {
const size = weight.length; // 物品的数量
const dp: number[][] = new Array(size + 1); // 创建一个二维数组来保存动态规划的状态
// 初始化二维数组
for (let i = 0; i <= size; i++) {
dp[i] = new Array(W + 1).fill(0);
}
// 枚举前 i 种物品
for (let i = 1; i <= size; i++) {
// 枚举背包装载重量
for (let w = 0; w <= W; w++) {
// 第 i - 1 件物品装不下
if (w < weight[i - 1]) {
// dp[i][w] 取「前 i - 1 件物品装入载重为 w 的背包中的最大价值」
dp[i][w] = dp[i - 1][w];
} else {
// dp[i][w] 取「前 i - 1 件物品装入载重为 w 的背包中的最大价值」与「前 i - 1 件物品装入载重为 w - weight[i - 1] 的背包中,再装入第 i - 1 物品所得的最大价值」两者中的最大值
dp[i][w] = Math.max(dp[i - 1][w], dp[i - 1][w - weight[i - 1]] + value[i - 1]);
}
}
}
// 返回最终的结果,即所有物品都考虑进去,且背包重量为 W 时的最大价值
return dp[size][W];
}
复杂度分析
- 时间复杂度:𝑂(𝑛×𝑊) ,其中 𝑛 为物品数量,𝑊 为背包的载重上限。
- 空间复杂度:𝑂(𝑛×𝑊) 。
0-1 背包问题算法题
HJ16 购物单
对于同一个物品,现在它的价格、重要度都是可变的 那么我们只需要对每一个主件尝试如下四种情况:
- 仅购买一个主件;
- 购买主件和第一个附件;
- 购买主件和第二个附件;
- 购买主件和两个附件;
在以上四种情况中找到最大值就能回归到0-1背包问题。
所以我们先考虑一下普通的0-1背包问题
对于一个可承重C的背包,我们假设所有物品的重量数据保存在w[],所有价值数据保存在v[]。那么我们有以下的推导式: $$ dp[i][j]=max(dp[i−1][j],dp[i−1][j−w[j]]+v[j]) $$ 那么对于“购物单”这道题,我们可以有如下抽象: $$ 不购买该物品: f[i−1][j] $$
$$ 仅购买一个主件: f[i−1][j−w[i]]+v[i]
$$
$$ 购买主件和第一个附件: f[i][j]=max(f[i−1][j],f[i−1][j−w[i]−w[a 1 ]]+v[i]+v[a 1 ])
$$
$$ 购买主件和第二个附件: f[i][j]=max(f[i−1][j],f[i−1][j−w[i]−w[a 2 ]]+v[i]+v[a 2 ]) $$
$$ 购买主件和两个附件: f[i][j]=max(f[i−1][j],f[i−1][j−w[i]−w[a 1 ]−w[a 2 ]]+v[i]+v[a 1 ]+v[a 2 ]) $$
用一个示例来说明,各个颜色表示最优方案,其中白块表示初始化区域,绿块表示不取物品最大,红块表示只取物品主件,紫块表示取物品主件和附件1,黄块表示取物品主件和附件2,蓝块表示取物品主件和两个附件 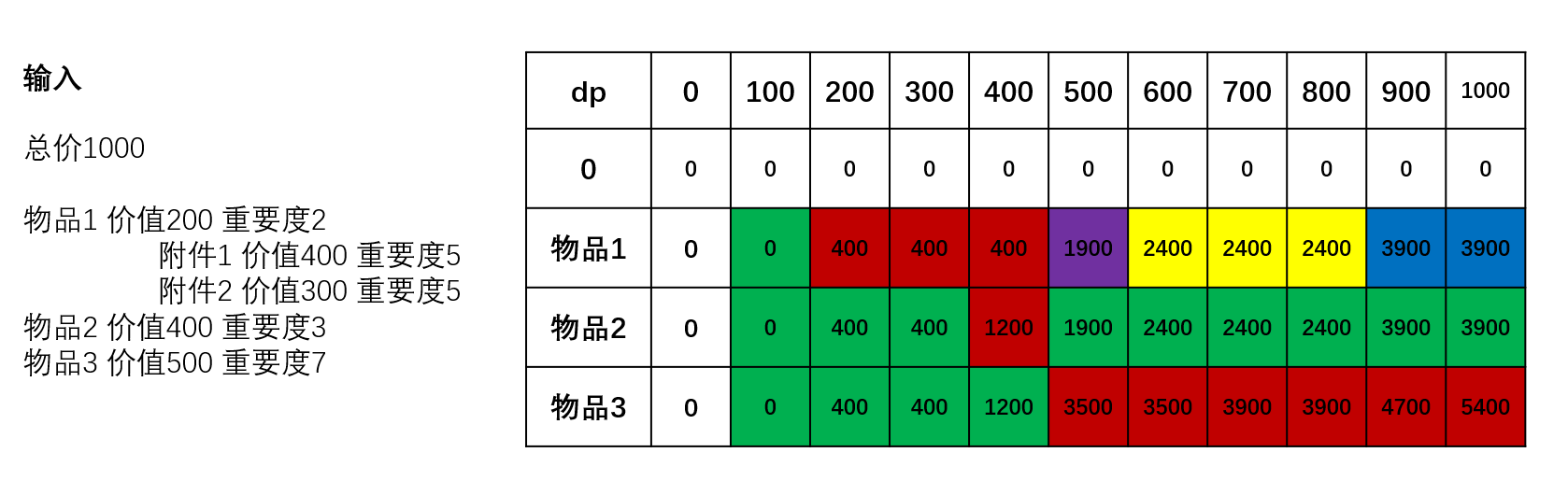
import * as readline from 'readline';
class Goods {
v: number;
p: number;
main: boolean;
a1: number;
a2: number;
constructor() {
this.v = 0;
this.p = 0;
this.main = false;
this.a1 = -1;
this.a2 = -1;
}
}
class Main {
public static main(args: string[]) {
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
const sc = rl.questionAsync('');
sc.then((N) => {
const m = parseInt(N, 10);
const goods = new Array(m).fill(0).map(() => new Goods());
for (let i = 0; i < m; i++) {
const v = parseInt(rl.question('')!, 10);
const p = parseInt(rl.question('')!, 10);
const q = parseInt(rl.question('')!, 10);
goods[i].v = v;
goods[i].p = p * v;
if (q === 0) {
goods[i].main = true;
} else {
if (goods[q - 1].a1 === -1) {
goods[q - 1].a1 = i;
} else {
goods[q - 1].a2 = i;
}
}
}
const dp = Array.from({ length: m + 1 }, () =>
Array(N + 1).fill(0)
);
for (let i = 1; i <= m; i++) {
for (let j = 0; j <= N; j++) {
dp[i][j] = dp[i - 1][j];
if (!goods[i - 1].main) {
continue;
}
if (j >= goods[i - 1].v) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - goods[i - 1].v] + goods[i - 1].p);
}
// ... 其他 if 条件分支与上面的类似,根据原始 Java 代码进行转换
}
}
console.log(dp[m][N]);
});
}
}
Main.main([]);