分治算法
分治算法
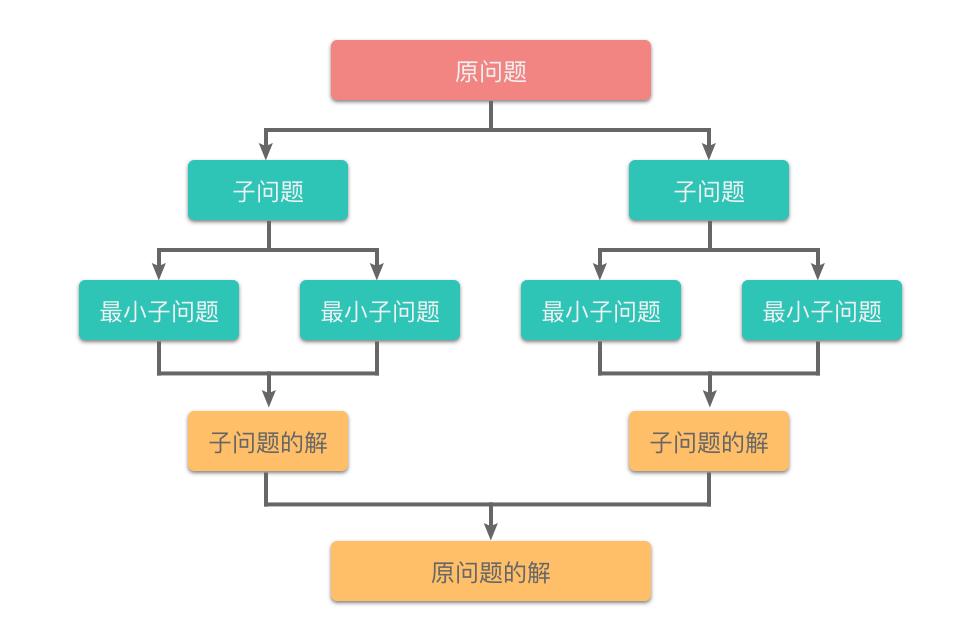
把规模大的问题不断分解为子问题,使得问题规模减小到可以直接求解为止。
分治算法和递归算法
从定义上来看,分治算法的思想和递归算法的思想是一样的,都是把规模大的问题不断分解为子问题。
其实,分治算法和递归算法的关系是包含与被包含的关系,可以看做: 递归算法 ∈ 分治算法。
分治算法从实现方式上来划分,可以分为两种:「递归算法」和「迭代算法」。
一般情况下,分治算法比较适合使用递归算法来实现。
但除了递归算法之外,分治算法还可以通过迭代算法来实现。比较常见的例子有:快速傅里叶变换算法、二分查找算法、非递归实现的归并排序算法等等。
分治算法的适用条件
分治算法能够解决的问题,一般需要满足以下 444 个条件:
- 可分解:原问题可以分解为若干个规模较小的相同子问题。
- 子问题可独立求解:分解出来的子问题可以独立求解,即子问题之间不包含公共的子子问题。
- 具有分解的终止条件:当问题的规模足够小时,能够用较简单的方法解决。
- 可合并:子问题的解可以合并为原问题的解,并且合并操作的复杂度不能太高,否则就无法起到减少算法总体复杂度的效果了。
分治算法的基本步骤
使用分治算法解决问题主要分为 333 个步骤:
- 分解:把要解决的问题分解为成若干个规模较小、相对独立、与原问题形式相同的子问题。
- 求解:递归求解各个子问题。
- 合并:按照原问题的要求,将子问题的解逐层合并构成原问题的解。
分治案例
算法题
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 0014 | 最长公共前缀 | 字典树、字符串 | 简单 |
| 0169 | 多数元素 | 数组、哈希表、分治、计数、排序 | 简单 |
| 0053 | 最大子数组和 | 数组、分治、动态规划 | 中等 |
| 0241 | 为运算表达式设计优先级 | 递归、记忆化搜索、数学、字符串、动态规划 | 中等 |
| 0050 | Pow(x, n) | 递归、数学 | 中等 |
| 剑指 Offer 33 | 二叉搜索树的后序遍历序列 | 栈、树、二叉搜索树、递归、二叉树、单调栈 | 中等 |
| 0004 | 寻找两个正序数组的中位数 | 数组、二分查找、分治 | 困难 |
| 0023 | 合并 K 个升序链表 | 链表、分治、堆(优先队列)、归并排序 | 困难 |
最长公共前缀
题解参考:字符串 | Sewen 博客 (sewar-x.github.io)
多数元素
题目
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
解法一:分治
思路
如果数 a 是数组 nums 的众数,如果我们将 nums 分成两部分,那么 a 必定是至少一部分的众数。
证明
使用反证法来证明这个结论:假设 a 既不是左半部分的众数,也不是右半部分的众数,那么 a 出现的次数少于 l / 2 + r / 2 次(其中 l 和 r 分别是左半部分和右半部分的长度)。由于 l / 2 + r / 2 <= (l + r) / 2,说明 a 也不是数组 nums 的众数,因此出现了矛盾。所以这个结论是正确的。
算法
- 分解:将数组分成左右两部分,分别求出左半部分的众数
a1以及右半部分的众数a2,随后在a1和a2中选出正确的众数。分解直到所有的子问题都是长度为1的数组。 - 求解:长度为
1的子数组中唯一的数显然是众数,直接返回即可。 - 合并:
- 如果回溯后某区间的长度大于
1,我们必须将左右子区间的值合并。 - 如果它们的众数相同,那么显然这一段区间的众数是它们相同的值。
- 否则,我们需要比较两个众数在整个区间内出现的次数来决定该区间的众数。
- 如果回溯后某区间的长度大于
function majorityElement(nums: number[]): number {
return majorityElementDiv(nums, 0, nums.length - 1)
};
/**
* 递归拆分
* @param nums
* @param start
* @param end
* @returns
*/
function majorityElementDiv(nums: number[], start: number, end: number): number {
//当拆分到只有一个元素时,返回当前元素
if (start === end) {
return nums[start]
}
// 计算中间值下标,从中间拆分
let mid = Math.floor((end + start) / 2)
// 递归拆分左半部分并计算出左半部分出现最多的数
let leftMaxNum = majorityElementDiv(nums, start, mid)
// 递归拆分右半部分并计算出右半部分出现最多的数
let rightMaxNum = majorityElementDiv(nums, mid + 1, end)
// 左右出现次数最多的数字相同,返回
if (leftMaxNum === rightMaxNum) {
return leftMaxNum
}
// 计算左侧出现次数最多的数字
let leftCount = countMaxTimeNum(nums, leftMaxNum, start, end)
// 计算右侧出现次数最多的数字
let rightCount = countMaxTimeNum(nums, rightMaxNum, start, end)
return leftCount > rightCount ? leftCount : rightCount
}
/**
* 统计在 [start,end] 范围内,num 在 nums 中出现次数
* @param nums
* @param num
* @param start
* @param end
* @returns
*/
function countMaxTimeNum(nums: number[], num: number, start: number, end: number): number {
let count = 0
for (let i = start; i <= end; i++) {
if (nums[i] === num) {
count++
}
}
return count
}
解法二:哈希表
- 遍历数组;
- 使用哈希表 map 存储每一个元素和它出现的次数,以元素为Key,元素出现次数为 value 存储;
- 遍历哈希表 map 中查找出现次数最多的元素,返回
function majorityElement(nums: number[]): number {
if (nums.length <= 2) return nums[0]
let numMap = new Map()
for (let i = 0; i < nums.length; i++) {
if (numMap.has(nums[i])) {
let num = numMap.get(nums[i])
num++
numMap.set(nums[i], num)
} else {
numMap.set(nums[i], 1)
}
}
let maxNum = 0
let maxNumKey = nums[0]
for (let [key, value] of numMap) {
if (value > maxNum) {
maxNum = value
maxNumKey = key
}
}
return maxNumKey
};
复杂度
- 时间复杂度:O(n) ,其中 n 是数组
nums的长度。 - 空间复杂度:O(n) 。
解法三:排序+中位数
如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序,那么下标为 n/2 的元素(下标从 0 开始)一定是众数。
function majorityElement(nums: number[]): number {
let sortNums = nums.sort((a,b)=> a-b)
return sortNums[Math.floor(nums.length/2)]
};
复杂度
时间复杂度:O(nlogn) 。将数组排序的时间复杂度为 O(nlogn) 。
空间复杂度:O(logn) 。如果使用语言自带的排序算法,需要使用 O(logn) 的栈空间。如果自己编写堆排序,则只需要使用 O(1) 的额外空间。
最大子数组和
题目
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
解法一:分治
使用分治法(Divide and Conquer)来解决“最大子数组和”问题,我们可以将数组分为两部分,然后递归地在这两部分中查找最大子数组和。但是,直接这样做并不能直接得到全局的最大子数组和,因为最大子数组可能跨越两个子数组的分界点。
因此,我们需要对分治法进行一些调整。在递归求解两个子数组的最大子数组和的同时,我们还需要计算跨越两个子数组分界点的子数组的和,即包含左边子数组末尾的一些元素和右边子数组开始的一些元素的子数组。
以下是使用分治法解决“最大子数组和”问题的详细步骤:
- 定义递归函数:
- 定义一个递归函数
findMaxCrossingSubarray(nums, low, mid, high),该函数用于查找跨越mid的最大子数组和 - 这个函数将返回跨越
mid的最大子数组的和、起始索引和结束索引。
- 定义一个递归函数
- 计算跨越分界点的最大子数组:
- 在
findMaxCrossingSubarray函数中,我们维护两个指针leftSum和rightSum,分别指向左子数组的末尾和右子数组的开头。 - 我们从
mid向左遍历,找到以mid结尾的最大子数组和leftSum,同时记录该子数组的起始索引maxLeft。 - 然后,我们从
mid+1向右遍历,找到以mid+1开头的最大子数组和rightSum,同时记录该子数组的结束索引minRight。 - 最后,返回
leftSum + rightSum、maxLeft和minRight。
- 在
- 递归求解子数组的最大子数组和:
- 对于整个数组
nums,我们首先找到中点mid,然后递归地在左子数组nums[low...mid]和右子数组nums[mid+1...high]中查找最大子数组和。
- 对于整个数组
- 合并结果:
- 我们比较三个值:左子数组的最大子数组和、右子数组的最大子数组和、以及跨越两个子数组分界点的最大子数组和。
- 取这三者中的最大值作为整个数组
nums[low...high]的最大子数组和。
- 基本情况:
- 当
low == high时,即子数组只包含一个元素时,直接返回该元素作为最大子数组和。
- 当
实现
function maxSubArray(nums: number[]): number {
const maxSubArr = findMaximumSubarray(nums, 0, nums.length - 1)
return maxSubArr.sum
};
// 查早最大子数组和
function findMaximumSubarray(nums: number[], low: number, high: number): { sum: number, start: number, end: number } {
if (low === high) {
return { sum: nums[low], start: low, end: high }; // 基本情况,只有一个元素
}
const mid = Math.floor((low + high) / 2);
// 递归求解左子数组的最大子数组和
const left = findMaximumSubarray(nums, low, mid);
// 递归求解右子数组的最大子数组和
const right = findMaximumSubarray(nums, mid + 1, high);
// 从中间数字开始计算跨越分界点的最大子数组和
const cross = findMaxCrossingSubarray(nums, low, mid, high);
// 合并结果,获取最大子数组和
if (left.sum >= right.sum && left.sum >= cross.sum) {
return left;
} else if (right.sum >= left.sum && right.sum >= cross.sum) {
return right;
} else {
return cross;
}
}
//查找跨越 mid 的最大子数组和
function findMaxCrossingSubarray(nums: number[], low: number, mid: number, high: number): { sum: number, start: number, end: number } {
let leftSum = -Infinity; //左子数组的末尾
let sum = 0;
let maxLeft = mid;
//从 `mid` 向左遍历,找到以 `mid` 结尾的最大子数组和 `leftSum`,同时记录该子数组的起始索引 `maxLeft`
for (let i = mid; i >= low; i--) {
sum += nums[i];
if (sum > leftSum) {
leftSum = sum;
maxLeft = i;
}
}
let rightSum = -Infinity; //右子数组的开头
sum = 0;
let minRight = mid + 1;
//我们从 `mid+1` 向右遍历,找到以 `mid+1` 开头的最大子数组和 `rightSum`,同时记录该子数组的结束索引 `minRight`
for (let i = mid + 1; i <= high; i++) {
sum += nums[i];
if (sum > rightSum) {
rightSum = sum;
minRight = i;
}
}
return { sum: leftSum + rightSum, start: maxLeft, end: minRight };
}
解法二:动态规划
思路
假设 nums 数组的长度是 n ,下标从 0 到 n−1 。
我们用 f(i) 代表以第 i 个数结尾的「连续子数组的最大和」,那么很显然我们要求的答案就是:
f(i)max (其中 0≤i≤n−1 ) 。
因此我们只需要求出每个位置的 f(i) ,然后返回 f 数组中的最大值即可。那么我们如何求 f(i) 呢?
我们可以考虑 nums[i] 单独成为一段还是加入 f(i−1) 对应的那一段,这取决于 nums[i] 和 f(i−1)+nums[i] 的大小,我们希望获得一个比较大的,于是可以写出这样的动态规划转移方程:
f(i)= max( f(i−1) + nums[i], nums[i] )
既 f(i) 的值取 f(i−1) + nums[i] 和 nums[i] 中较大的值。
算法
- 初始化变量:
pre:表示以当前元素为结尾的子数组的最大和。初始时,pre被设为数组的第一个元素nums[0]。maxAns:表示遍历过程中遇到的所有子数组的最大和。初始时,maxAns也被设为数组的第一个元素nums[0]。
- 遍历数组,对于数组中的每一个元素
nums[i]:- 计算以
nums[i]为结尾的子数组的最大和。这个最大和要么是nums[i]本身(即新的子数组只包含一个元素),要么是pre + nums[i](即把nums[i]加到之前子数组的末尾)。选择两者中的较大值作为新的pre。 - 更新
maxAns。比较当前的maxAns和pre,将两者中的较大值赋给maxAns。这样,maxAns始终保存了遍历过程中遇到的最大子数组和。
- 计算以
实现
var maxSubArray = function(nums) {
//pre:表示以当前元素为结尾的子数组的最大和
let pre = 0
//maxAns:表示遍历过程中遇到的所有子数组的最大和
let maxAns = nums[0];
nums.forEach((x) => {
//计算以 nums[i] 为结尾的子数组的最大和, 与 nums[i]比较,选择两者中的较大值作为新的 pre。
pre = Math.max(pre + x, x);
// 比较以 nums[i] 为结尾的数组的最大和 与 遍历过程中遇到的所有子数组的最大和 的大小,选择较大的作为maxAns
maxAns = Math.max(maxAns, pre);
});
return maxAns;
};
以输入数组
nums = [-2,1,-3,4,-1,2,1,-5,4]为例:
- 初始时,
pre = 0, maxAns = -2(注意这里实际上应该初始化为nums[0] = -2,但代码中直接用了0作为起点并不会影响最终结果,因为第一个元素会被遍历到)。- 遍历到
1:pre = max(0 + 1, 1) = 1,maxAns = max(-2, 1) = 1。- 遍历到
-3:pre = max(1 - 3, -3) = -3,maxAns保持为1。- 遍历到
4:pre = max(-3 + 4, 4) = 4,maxAns = max(1, 4) = 4。- ... 以此类推,直到遍历完整个数组。
最终,
maxAns的值为6,即最大子数组[4,-1,2,1]的和。