回溯算法
回溯算法

思想
采用试错的思想,在搜索尝试过程中寻找问题的解,当探索到某一步时,发现原先的选择并不满足求解条件,或者还需要满足更多求解条件时,就退回一步(回溯)重新选择,这种走不通就退回再走的技术称为「回溯法」,而满足回溯条件的某个状态的点称为「回溯点」。
回溯算法采用了一种 「走不通就回退」 的算法思想。
回溯算法通常用简单的递归方法来实现,在进行回溯过程中更可能会出现两种情况:
- 找到一个可能存在的正确答案;
- 在尝试了所有可能的分布方法之后宣布该问题没有答案。
回溯算法解题步骤
回溯算法的基本思想是:以深度优先搜索的方式,根据产生子节点的条件约束,搜索问题的解。当发现当前节点已不满足求解条件时,就「回溯」返回,尝试其他的路径。
在写回溯算法时具体步骤如下:
- 定义问题解空间:
- 明确问题的解空间,即所有可能的解或候选解的集合。
- 解空间树是回溯法求解过程中组织搜索的一个数据结构。树上的每一个节点表示问题求解过程中可能到达的一个中间状态,它包含有关搜索路径和求得中间解的全部信息。
- 确定搜索策略:
- 选择合适的搜索策略,如**深度优先搜索或广度优先搜索。**在回溯法中,通常使用深度优先搜索。
- 确定搜索的起始点和结束条件。
- 设计递归函数:
- 设计一个或多个递归函数,用于遍历解空间树。
- 递归函数应接收当前路径(当前解的部分表示)和当前搜索状态(如当前节点的索引)作为参数。
- 剪枝优化:
- 在搜索过程中,如果发现当前搜索路径的某个节点不可能导出问题的解,则应及时停止对该节点的进一步搜索,即“剪枝”。
- 剪枝可以显著提高算法的效率,减少不必要的搜索。
- 回溯:
- 当搜索到某一节点时,如果已不满足求解条件,就“退回”一步(即回溯),尝试其他可能。
- 回溯操作通常涉及撤销在当前节点所做的选择,并返回到其父节点或前一个状态。
- 存储和输出结果:
- 当找到一个有效解时,将其存储起来(例如,添加到结果列表中)。
- 在所有可能的解都被找到后,输出或返回结果。
- 处理边界条件和特殊情况:
- 在编写回溯算法时,要注意处理边界条件和特殊情况。
- 例如,当搜索到解空间的边界时,可能需要特殊处理;当某些选择无效或导致重复解时,需要跳过这些选择。
回溯算法的通用模板
// 假设有一个目标函数用于判断某个路径是否满足条件
function isValid(path, currentChoice) {
// 在这里编写你的逻辑,判断当前选择是否有效
// 返回true表示有效,返回false表示无效
// 例如,如果我们在解决组合问题,可能会检查路径是否已包含当前选择
}
/*
回溯函数
choices:表示当前层可以选择的选项列表。
path:表示从根节点到当前节点的路径。默认为空数组。
start:表示从哪个索引开始选择。默认为0,但在某些问题中,你可能希望从某个特定的索引开始以避免重复。
**/
function backtrack(choices, path = [], start = 0) {
//这是一个你需要定义的函数或逻辑,用于判断何时停止在当前路径上进一步探索
// 如果满足某种条件(例如,路径长度达到目标长度),则记录或处理路径
if (满足结束条件(path)) {
// 例如,将路径添加到结果集中
results.push(path.slice()); // 注意:使用slice()创建路径的副本,避免直接修改原数组
}
//遍历当前层的所有选择
for (let i = start; i < choices.length; i++) {
// 做选择
const currentChoice = choices[i];
// 判断当前选择是否有效
if (isValid(path, currentChoice)) {
// 将当前选择添加到路径中
path.push(currentChoice);
// 进入下一层决策树
backtrack(choices, path, i + 1); // 注意:在某些问题中,可能需要从i+1开始以避免重复
// 撤销选择,无论是否进入下一层,都需要撤销当前选择,以便在for循环的下一轮尝试其他选择。
path.pop();
}
}
}
// 初始化结果集和选择列表
let results = [];
let choices = [...]; // 填充你的选择列表
// 调用回溯函数
backtrack(choices);
// 打印结果
console.log(results);
详细解释:
- isValid函数:这是一个辅助函数,用于判断某个选择在当前路径下是否有效。你需要根据问题的具体需求来实现这个函数。
- backtrack函数:这是回溯算法的核心函数。
- 参数:
choices:表示当前层可以选择的选项列表。path:表示从根节点到当前节点的路径。默认为空数组。start:表示从哪个索引开始选择。默认为0,但在某些问题中,你可能希望从某个特定的索引开始以避免重复。
- 满足结束条件:这是一个你需要定义的函数或逻辑,用于判断何时停止在当前路径上进一步探索。例如,在组合问题中,你可能希望当路径长度达到某个目标值时停止。
- for循环:遍历当前层的所有选择。
- 做选择:将当前选择添加到路径中。
- 判断有效性:使用
isValid函数检查当前选择是否有效。 - 递归调用:如果当前选择有效,则进入下一层决策树。注意,在某些问题中,你可能需要从
i+1开始以避免重复选择。 - 撤销选择:无论是否进入下一层,都需要撤销当前选择,以便在for循环的下一轮尝试其他选择。
- 参数:
- 结果集和选择列表:在调用
backtrack函数之前,你需要初始化结果集和选择列表。结果集用于存储所有满足条件的路径,选择列表包含所有可能的选项。 - 调用回溯函数并打印结果:最后,调用
backtrack函数并打印结果集。
算法题
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 0046 | 全排列 | 数组、回溯 | 中等 |
| 0047 | 全排列 II | 数组、回溯 | 中等 |
| 0051 | N皇后 | 数组、回溯 | 困难 |
| 0037 | 解数独 | 数组、哈希表、回溯、矩阵 | 困难 |
| 0022 | 括号生成 | 字符串、动态规划、回溯 | 中等 |
| 0017 | 电话号码的字母组合 | 哈希表、字符串、回溯 | 中等 |
| 0784 | 字母大小写全排列 | 位运算、字符串、回溯 | 中等 |
| 0039 | 组合总和 | 数组、回溯 | 中等 |
| 0040 | 组合总和 II | 数组、回溯 | 中等 |
| 0078 | 子集 | 位运算、数组、回溯 | 中等 |
| 0090 | 子集 II | 位运算、数组、回溯 | 中等 |
| 0473 | 火柴拼正方形 | 位运算、数组、动态规划、回溯、状态压缩 | 中等 |
| 1593 | 拆分字符串使唯一子字符串的数目最大 | 哈希表、字符串、回溯 | 中等 |
| 1079 | 活字印刷 | 哈希表、字符串、回溯、计数 | 中等 |
| 0093 | 复原 IP 地址 | 字符串、回溯 | 中等 |
| 0079 | 单词搜索 | 数组、回溯、矩阵 | 中等 |
| 0679 | 24 点游戏 | 数组、数学、回溯 | 困难 |
全排列
题目
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
解法一:回溯
思路
以求解 [1,2,3] 的全排列为例,我们来讲解一下回溯算法的过程:
- 选择以 1 为开头的全排列:
- 选择以 2 为中间数字的全排列,则最后数字只能选择 3 。即排列为: [1,2,3]。
- 撤销选择以 3 为最后数字的全排列,再撤销选择以 2 为中间数字的全排列。
- 然后选择以 3 为中间数字的全排列,则最后数字只能选择 2 ,即排列为 [1,3,2]。
- 撤销选择以 2 为最后数字的全排列,再撤销选择以 3 为中间数字的全排列,再撤销选择以 1为开头的全排列。然后选择以 2 开头的全排列:
- 选择以 1 为中间数字的全排列,则最后数字只能选择 3 。即排列为: [2,1,3]。
- 撤销选择以 3 为最后数字的全排列,再撤销选择以 1 为中间数字的全排列。
- 然后选择以 3 为中间数字的全排列,则最后数字只能选择 1 ,即排列为: [2,3,1]。
- 撤销选择以 1 为最后数字的全排列,再撤销选择以 3 为中间数字的全排列,再撤销选择以 2 为开头的全排列,选择以 3 开头的全排列:
- 选择以 1 为中间数字的全排列,则最后数字只能选择 2 。即排列为: [3,1,2]。
- 撤销选择以 2 为最后数字的全排列,再撤销选择以 1 为中间数字的全排列。
- 然后选择以 2 为中间数字的全排列,则最后数字只能选择 1 ,即排列为: [3,2,1]。
总结一下全排列的回溯过程:
- 按顺序枚举每一位上可能出现的数字,之前已经出现的数字在接下来要选择的数字中不能再次出现。
- 对于每一位 进行如下几步:
- 选择元素:从可选元素列表中选择一个之前没有出现过的元素。
- 递归搜索:从选择的元素出发,一层层地递归搜索剩下位数,直到遇到边界条件时,不再向下搜索。
- 撤销选择:一层层地撤销之前选择的元素,转而进行另一个分支的搜索。直到完全遍历完所有可能的路径。
对于上述决策过程,我们也可以用一棵决策树来表示:
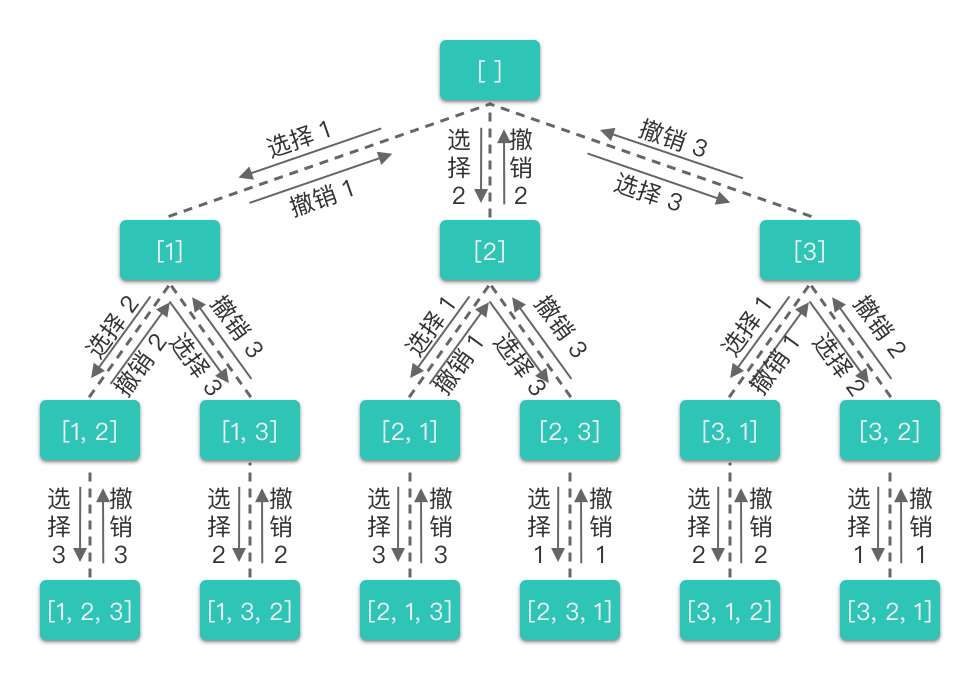
从全排列的决策树中我们可以看出:
- 每一层中有一个或多个不同的节点,这些节点以及节点所连接的分支代表了「不同的选择」。
- 每一个节点代表了求解全排列问题的一个「状态」,这些状态是通过「不同的值」来表现的。
- 每向下递推一层就是在「可选元素列表」中选择一个「元素」加入到「当前状态」。
- 当一个决策分支探索完成之后,会逐层向上进行回溯。
- 每向上回溯一层,就是把所选择的「元素」从「当前状态」中移除,回退到没有选择该元素时的状态(或者说重置状态),从而进行其他分支的探索。
实现
function permute(nums: number[]): number[][] {
const results: number[][] = []; // 存储所有排列结果的数组
const used: boolean[] = new Array(nums.length).fill(false); // 标记数组,用于追踪元素是否被使用
// 回溯函数
function backtrack(path: number[]): void {
// 如果路径长度等于 nums 长度,说明找到了一种排列,将其添加到结果中
if (path.length === nums.length) {
results.push(path.slice()); // 使用 slice() 创建新数组,避免后续修改影响结果
return;
}
for (let i = 0; i < nums.length; i++) {
// 如果当前元素没有被使用过
if (!used[i]) {
// 将当前元素添加到路径中
path.push(nums[i]);
// 标记当前元素为已使用
used[i] = true;
// 继续回溯,尝试下一个位置,使用深度优先搜索查找未使用的数字,组成一个全排列
backtrack(path);
// 回溯到上一个状态:移除当前元素,并标记为未使用
path.pop();
used[i] = false;
}
}
}
// 调用回溯函数,从空路径开始
backtrack([]);
// 返回所有排列结果
return results;
}
复杂度分析
时间复杂度为 O(n!):
时间复杂度主要取决于递归的调用次数和每次递归所做的操作。因为对于长度为
n的数组nums,我们需要生成n!(n 的阶乘)个排列。在回溯过程中,对于每个位置,我们都有n个选择(在第一次递归时),然后是n-1个选择(在第二次递归时),依此类推,直到没有选择。因此,总的递归调用次数是n!。每次递归调用中,我们都需要遍历数组
nums来查找未使用的元素,这个操作的时间复杂度是 O(n)。但是,由于递归树的深度是 n,并且每次递归都会遍历数组的一部分(从 n 到 1),所以我们可以将遍历的总时间视为 O(n * n!)。然而,考虑到主要的开销在于递归调用本身(即生成所有排列),我们通常只考虑n!的部分,因此时间复杂度为 O(n!)。
空间复杂度为 O(n * n!):
- 空间复杂度主要由递归调用栈和存储结果的数组决定。
- 递归调用栈:在最坏的情况下(即生成所有排列时),递归调用栈的深度可以达到 n。因此,递归调用栈的空间复杂度是 O(n)。
- 存储结果的数组:我们需要一个二维数组来存储所有的排列。在最坏的情况下,这个数组将包含
n!个长度为 n 的一维数组。因此,存储结果的空间复杂度是 O(n * n!)。但是,由于n!是主导项,我们通常只考虑n!的部分。 - 临时变量和标记数组:
path数组和used数组的大小都是 O(n),但它们不随输入规模的增长而呈指数级增长,因此可以忽略不计。
- 空间复杂度主要由递归调用栈和存储结果的数组决定。
解法二:枚举
思路
记原序列中元素的总数为 n 。原序列中的每个数字的状态可能有两种,即「在子集中」和「不在子集中」。
我们用 1 表示「在子集中」,0 表示不在子集中,那么每一个子集可以对应一个长度为 n 的 0/1 序列,第 i 位表示 a[i] 是否在子集中。例如:n=3 ,a={5,2,9} 时:
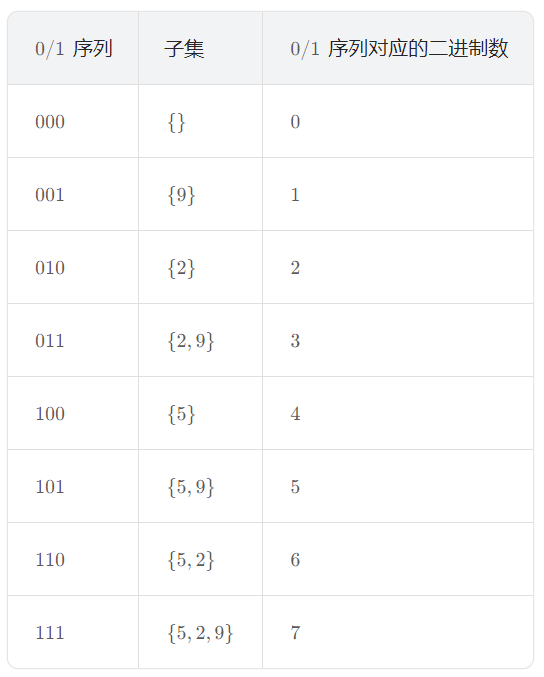
可以发现 0/1 序列对应的二进制数正好从 0 到 2^n - 1 。
我们可以枚举 mask∈[0,2^n−1], mask 的二进制表示是一个 0/1 序列,我们可以按照这个 0/1 序列在原集合当中取数。当我们枚举完所有 2^n 个 mask ,我们也就能构造出所有的子集。
解题思路:
- 二进制掩码:为了生成一个数组的所有子集,我们可以使用一个二进制掩码(即一个整数)。这个掩码的每一位都对应于数组
nums的一个元素。如果掩码的某一位是 1,那么nums中对应位置的元素就是当前子集的一部分。 - 遍历所有掩码:我们遍历从 0 到
2^n - 1的所有整数,其中 n 是nums的长度。这些整数在二进制表示下可以看作是不同的掩码。例如,当 n=3 时,我们遍历 000, 001, 010, 011, 100, 101, 110, 111,分别对应于空集,只包含第一个元素,只包含第二个元素,包含第一和第二个元素,以此类推。 - 生成子集:对于每个掩码,我们遍历
nums数组,并使用位运算来检查掩码的每一位。如果某一位是 1,则将对应的元素添加到当前子集中。 - 收集结果:将每个生成的子集添加到结果数组
ans中,并在遍历完所有掩码后返回ans。
这种方法利用了位运算和二进制掩码的概念,以高效的方式生成了数组的所有子集。
实现
// 定义函数 subsets,它接受一个数组 nums 作为参数,并返回 nums 的所有子集
var subsets = function(nums) {
// 初始化一个空数组 ans,用于存储所有子集
const ans = [];
// 获取 nums 数组的长度
const n = nums.length;
// 遍历从 0 到 2^n - 1 的所有整数(二进制表示),因为每个整数都可以看作是一个二进制掩码
// 这些二进制掩码用于选择 nums 中的元素以生成不同的子集
for (let mask = 0; mask < (1 << n); ++mask) {
// 初始化一个空数组 t,用于存储当前掩码对应的子集
const t = [];
// 遍历 nums 数组的每个元素
for (let i = 0; i < n; ++i) {
// 使用位运算来检查 mask 的第 i 位是否为 1
// 如果是 1,则 nums[i] 是当前子集的一部分
if (mask & (1 << i)) {
// 将 nums[i] 添加到当前子集 t 中
t.push(nums[i]);
}
}
// 将当前子集 t 添加到结果数组 ans 中
ans.push(t);
}
// 返回包含所有子集的数组 ans
return ans;
};
1<<n和1<<i是位运算符在编程中的使用,特别是左移(<<)运算符。在这些表达式中,
1是一个二进制数,具体表示为000...0001(假设有足够的前导零以匹配n或i的位数)。左移运算符
<<将数字的所有位向左移动指定的位数。原理
- 1 的二进制表示:在二进制中,数字
1通常表示为000...0001,其中只有一个位是1,其余都是0。这个1通常位于最低位(也称为最右边)。- 左移运算符(
<<):左移运算符将数字的所有位向左移动指定的位数。在左侧空出的位置用0填充。示例
假设我们有一个 8 位的二进制数,并且我们想要将
1左移3位(即1<<3)。原始的
1(8 位表示):00000001左移 3 位后:00100000
在这个例子中,
1被移动到了左侧 3 位的位置,并且在左侧空出的位置填充了0。对于
1<<n或1<<i,n或i就是你要将1左移的位数。因此,1<<n将产生一个二进制数,其中只有第n位(从右边开始计数,从 0 开始)是1,其余都是0。这个数在十进制下等于 (2^n)。这种操作在编程中经常用于生成位掩码(bitmask)或执行位操作,特别是当你需要快速地设置、清除或检查某个特定位时。
全排列 II
题目
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
解法:回溯
为了解决这个问题,我们可以使用回溯算法(也称为深度优先搜索DFS)来生成所有可能的全排列。
但是,由于输入序列 nums 可能包含重复数字,我们需要一种方法来避免生成重复的全排列。
解题思路如下:
- 排序:首先,对数组
nums进行排序。这一步不是必需的,但它可以帮助我们更容易地跳过重复的全排列。 - 回溯:使用回溯算法来生成所有可能的全排列。
- 跳过重复的全排列:在回溯过程中,当我们选择一个数字加入当前排列时,我们需要检查这个数字是否与它前面的数字(在同一个层级,而不是递归的父层级)相同,并且前一个数字没有被使用过。如果这两个条件都满足,我们就跳过这个数字,因为它会导致一个与前面已经生成的全排列相同的结果。
实现
function permuteUnique(nums: number[]): number[][] {
// 排序数组,以便更容易地跳过重复的全排列
nums.sort((a, b) => a - b);
// 全排列结果
const result: number[][] = [];
// 标记 nums[i] 是否被使用
const used: boolean[] = new Array(nums.length).fill(false);
// 从空数组开始回溯
backtrack(nums, [], used, result);
return result;
}
function backtrack(nums: number[], path: number[], used: boolean[], result: number[][]) {
// 当当前排列的长度等于原始数组的长度时,将其添加到结果中
if (path.length === nums.length) {
result.push([...path]); // 注意这里需要使用展开运算符来复制数组
return;
}
// 每次回溯时,从第一个数字开始搜素未被使用的数字进行回溯
for (let i = 0; i < nums.length; i++) {
// 跳过已经使用过的数字
if (used[i]) continue;
// 跳过重复的数字(只比较相邻的未使用过的数字)
if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) continue;
// 选择当前数字
used[i] = true;
path.push(nums[i]);
// 递归生成下一个位置的全排列
backtrack(nums, path, used, result);
// 回溯,撤销选择
used[i] = false;
path.pop();
}
}