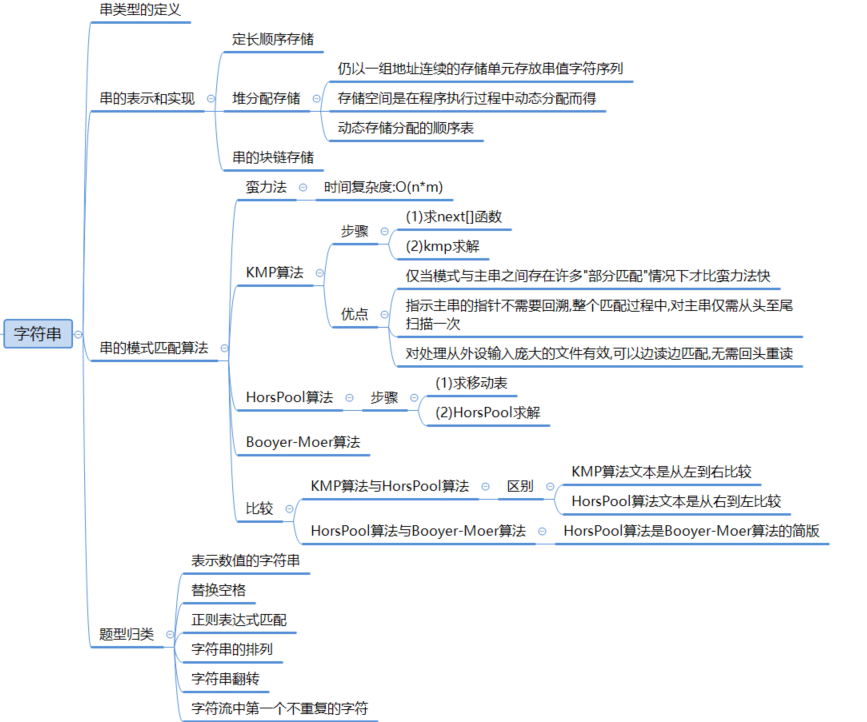
字符串
字符串
基础
JavaScript 字符串基础参考:JavaScript 基础 | Sewen 博客 (sewar-x.github.io)
定义
空串:空串指的是未存储任何字符的串,整个串的长度为 0。
空格串:空格串指的是由多个(>0)空格字符组成的串结构,整个串的长度为包含空格字符的个数。
子串和主串:
假设有以下两个串 A 和 B: A:shujujiegou B:shuju在串 A 中可以找到几个连续的字符,它们和串 B 相同。我们可以这样描述它们之间的关系:A 是 B 的主串,B 是 A 的子串。
- 注意:子串在主串中的位置,指的是子串首个字符在主串中的位置。
- 例如,串 A 为 "shujujiegou",串 B 为 "jiegou",通过观察可以判断 A、B 是主串和子串的关系,即在主串 A 中可以找到 B,B 的第一个字符 'j' 是串 A 中的第 6 个字符,因此子串 B 在主串 A 中的位置就是 6。
- 注意:子串在主串中的位置,指的是子串首个字符在主串中的位置。
字符串相关问题
- 字符串匹配问题。
- 子串相关问题。
- 前缀 / 后缀相关问题;
- 回文串相关问题。
- 子序列相关问题。
字符串的比较
/**
* 字符串比较函数,类似于 C 标准库中的 strcmp 函数。
*
* @param str1 第一个待比较的字符串
* @param str2 第二个待比较的字符串
* @returns 如果 str1 < str2,返回 -1;如果 str1 > str2,返回 1;如果 str1 == str2,返回 0
*/
function strcmp(str1: string, str2: string): number {
let index1 = 0; // str1 的索引
let index2 = 0; // str2 的索引
// 当两个字符串均未遍历完时,继续比较
while (index1 < str1.length && index2 < str2.length) {
// 获取当前索引位置的字符的 Unicode 编码并进行比较
if (str1.charCodeAt(index1) === str2.charCodeAt(index2)) {
// 如果编码相等,则两个字符相等,继续比较下一个字符
index1++;
index2++;
} else if (str1.charCodeAt(index1) < str2.charCodeAt(index2)) {
// 如果 str1 当前字符的编码小于 str2 当前字符的编码,则 str1 < str2
return -1;
} else {
// 否则,str1 当前字符的编码大于 str2 当前字符的编码,则 str1 > str2
return 1;
}
}
// 如果其中一个字符串已经遍历完,而另一个还有剩余字符,则长度较短的字符串较小
if (str1.length < str2.length) {
return -1;
} else if (str1.length > str2.length) {
return 1;
}
// 如果两个字符串都遍历完且长度相等,则两个字符串相等
return 0;
}
判断两个字符串是否相等
- 字符串 𝑠𝑡𝑟1 和字符串 𝑠𝑡𝑟2 的长度相等。
- 字符串 𝑠𝑡𝑟1 和字符串 𝑠𝑡𝑟2 对应位置上的各个字符都相同。
判断两个字符串的大小
对于两个不相等的字符串,我们可以以下面的规则定义两个字符串的大小:
- 从两个字符串的第 0 个位置开始,依次比较对应位置上的字符编码大小。
- 如果 𝑠𝑡𝑟1[𝑖] 对应的字符编码等于 𝑠𝑡𝑟2[𝑖] 对应的字符编码,则比较下一位字符。
- 如果 𝑠𝑡𝑟1[𝑖] 对应的字符编码小于 𝑠𝑡𝑟2[𝑖] 对应的字符编码,则说明 𝑠𝑡𝑟1<𝑠𝑡𝑟2。比如:
"abc" < "acc"。 - 如果 𝑠𝑡𝑟1[𝑖] 对应的字符编码大于 𝑠𝑡𝑟2[𝑖] 对应的字符编码,则说明 𝑠𝑡𝑟1>𝑠𝑡𝑟2。比如:
"bcd" > "bad"。
- 如果比较到某一个字符串末尾,另一个字符串仍有剩余:
- 如果字符串 𝑠𝑡𝑟1 的长度小于字符串 𝑠𝑡𝑟2,即 𝑙𝑒𝑛(𝑠𝑡𝑟1)<𝑙𝑒𝑛(𝑠𝑡𝑟2)。则 𝑠𝑡𝑟1<𝑠𝑡𝑟2。比如:
"abc" < "abcde"。 - 如果字符串 𝑠𝑡𝑟1 的长度大于字符串 𝑠𝑡𝑟2,即 𝑙𝑒𝑛(𝑠𝑡𝑟1)>𝑙𝑒𝑛(𝑠𝑡𝑟2)。则 𝑠𝑡𝑟1>𝑠𝑡𝑟2。比如:
"abcde" > "abc"。
- 如果字符串 𝑠𝑡𝑟1 的长度小于字符串 𝑠𝑡𝑟2,即 𝑙𝑒𝑛(𝑠𝑡𝑟1)<𝑙𝑒𝑛(𝑠𝑡𝑟2)。则 𝑠𝑡𝑟1<𝑠𝑡𝑟2。比如:
- 如果两个字符串每一个位置上的字符对应的字符编码都相等,且长度相同,则说明 𝑠𝑡𝑟1==𝑠𝑡𝑟2,比如:
"abcd" == "abcd"。
按照上面的规则,我们可以定义一个 strcmp 方法,并且规定:
- 当 𝑠𝑡𝑟1<𝑠𝑡𝑟2 时,
strcmp方法返回 −1。 - 当 𝑠𝑡𝑟1==𝑠𝑡𝑟2 时,
strcmp方法返回 0。 - 当 𝑠𝑡𝑟1>𝑠𝑡𝑟2 时,
strcmp方法返回 1。
字符串匹配
字符串匹配问题
字符串匹配(String Matching):又称模式匹配(Pattern Matching)。可以简单理解为,给定字符串 𝑇 和 𝑝,在主串 𝑇 中寻找子串 𝑝。主串 𝑇 又被称为文本串,子串 𝑝 又被称为模式串(
Pattern)。
在字符串问题中,最重要的问题之一就是字符串匹配问题。
而按照模式串的个数,我们可以将字符串匹配问题分为:「单模式串匹配问题」和「多模式串匹配问题」。
单模式串匹配问题
单模式匹配问题(Single Pattern Matching):给定一个文本串 𝑇=𝑡1𝑡2...𝑡𝑛,再给定一个特定模式串 𝑝=𝑝1𝑝2...𝑝𝑛。
要求从文本串 𝑇 找出特定模式串 𝑝 的所有出现位置。
有很多算法可以解决单模式匹配问题。而根据在文本中搜索模式串方式的不同,我们可以将单模式匹配算法分为以下几种:
基于前缀搜索方法:
- 在搜索窗口内从前向后(沿着文本的正向)逐个读入文本字符,搜索窗口中文本和模式串的最长公共前缀。
- 著名的「 (KMP) 算法」和更快的「Shift-Or 算法」使用的就是这种方法。
基于后缀搜索方法:
- 在搜索窗口内从后向前(沿着文本的反向)逐个读入文本字符,搜索窗口中文本和模式串的最长公共后缀。使用这种搜索算法可以跳过一些文本字符,从而具有亚线性的平均时间复杂度。
- 最著名的「Boyer-Moore 算法」,以及「Horspool 算法」、「Sunday(Boyer-Moore 算法的简化)算法」都使用了这种方法。
基于子串搜索方法:
- 在搜索窗口内从后向前(沿着文本的反向)逐个读入文本字符,搜索满足「既是窗口中文本的后缀,也是模式串的子串」的最长字符串。与后缀搜索方法一样,使用这种搜索方法也具有亚线性的平均时间复杂度。这种方法的主要缺点在于需要识别模式串的所有子串,这是一个非常复杂的问题。
- 「Rabin-Karp 算法」、「Backward Dawg Matching(BDM)算法」、「Backward Nondeterministtic Dawg Matching(BNDM)算法」和 「Backward Oracle Matching(BOM)算法」 使用的就是这种思想。其中,「Rabin-Karp 算法」使用了基于散列的子串搜索算法。
多模式串匹配问题
多模式匹配问题(Multi Pattern Matching):给定一个文本串 𝑇=𝑡1𝑡2...𝑡𝑛,再给定一组模式串 𝑃=𝑝1,𝑝2,...,𝑝𝑟,其中每个模式串 𝑝𝑖 是定义在有限字母表上的字符串 𝑝𝑖=𝑝1𝑖𝑝2𝑖...𝑝𝑛𝑖。
要求从文本串 𝑇 中找到模式串集合 𝑃 中所有模式串 𝑝𝑖 的所有出现位置。
模式串集合 𝑃 中的一些字符串可能是集合中其他字符串的子串、前缀、后缀,或者完全相等。
解决多模式串匹配问题最简单的方法是利用「单模式串匹配算法」搜索 𝑟 遍。这将导致预处理阶段的最坏时间复杂度为 𝑂(|𝑃|),搜索阶段的最坏时间复杂度为 𝑂(𝑟×𝑛)。
如果使用「单模式串匹配算法」解决多模式匹配问题,那么根据在文本中搜索模式串方式的不同,我们也可以将多模式串匹配算法分为以下三种:
基于前缀搜索方法:
搜索从前向后(沿着文本的正向)进行,逐个读入文本字符,使用在 𝑃 上构建的自动机进行识别。对于每个文本位置,计算既是已读入文本的后缀,同时也是 𝑃 中某个模式串的前缀的最长字符串。
著名的 「Aho-Corasick Automaton(AC 自动机)算法」、「Multiple Shift-And 算法」使用的这种方法。
基于后缀搜索方法:
- 搜索从后向前(沿着文本的反向)进行,搜索模式串的后缀。根据后缀的下一次出现位置来移动当前文本位置。这种方法可以避免读入所有的文本字符。
- 「Commentz-Walter(Boyer-Moore 算法的扩展算法)算法」 、「Set Horspool(Commentz-Walter 算法的简化算法)算法」、「Wu-Manber 算法」都使用了这种方法。
基于子串搜索方法:
- 搜索从后向前(沿着文本的反向)进行,在模式串的长度为 𝑚𝑖𝑛(𝑙𝑒𝑛(𝑝𝑖)) 的前缀中搜索子串,以此决定当前文本位置的移动。这种方法也可以避免读入所有的文本字符。
- 「Multiple BNDM 算法」、「Set Backward Dawg Matching(SBDM)算法」、「Set Backwrad Oracle Matching(SBOM)算法」都使用了这种方法。
需要注意的是,以上所介绍的多模式串匹配算法大多使用了一种基本的数据结构:「字典树(Trie Tree)」。著名的 「Aho-Corasick Automaton (AC 自动机) 算法」 就是在「KMP 算法」的基础上,与「字典树」结构相结合而诞生的。而「AC 自动机算法」也是多模式串匹配算法中最有效的算法之一。
所以学习多模式匹配算法,重点是要掌握 「字典树」 和 「AC 自动机算法」 。
单模式串匹配
串的模式匹配算法,是一种专门定位子串在主串中位置的方法(方案、思想),整个定位的过程称为模式匹配。
此外,在模式匹配的过程中,子串通常又被称为“模式串”。
示例:
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。
如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = "sadbutsad", needle = "sad" 输出:0 解释:"sad" 在下标 0 和 6 处匹配。 第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = "leetcode", needle = "leeto" 输出:-1 解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。提示:
1 <= haystack.length, needle.length <= 104 haystack 和 needle 仅由小写英文字符组成
BF 算法(蛮力法)
- 思路:
采用 BF 算法定位模式串在主串中的位置,就是简单粗暴的从主串的起始位置开始,不断地将模式串中的字符和主串中的字符进行对比。
设置两个指针,分别循环遍历主串和字串,将主串和字串一一对应匹配;
- 如果匹配成功,同时后移一位;
- 如果匹配失败,主串从下个字符开始匹配,字串从头开始匹配;
遍历结束,如果字串遍历到末尾,表示匹配成功,返回主串指针位置减去字串长度加1,即为字串的初始位置;否则匹配失败;
示例:
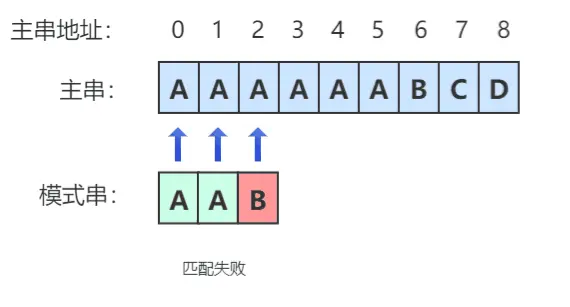
假设对模式串 A("abcac")和主串 B("ababcabacabab")进行模式匹配,BF 算法的执行过程如下:
将模式串 A 与主串 B 的首字符对齐,逐个判断相对的字符是否相等,如
图 1 中,由于模式串 A 与主串 B 的第 3 个字符匹配失败,此时将模式串 A 后移一个字符的位置,采用同样的方法重新匹配,如图 2 所示:
图 2 中可以看到,两个串依旧匹配失败,模式串 A 继续后移一个字符的位置,如图 3 所示:
图 3 仍然匹配失败,模式串 A 继续向后移动,一直移动至图 4 的位置才匹配成功:
从图 1 到图 4,模式串 A 与主串 B 共匹配了 6 次才成功,最终定位到模式串 A 位于主串 B 第 6 的位置处,整个模式匹配的过程就称为 BF 算法。
示例2:
时间复杂度:O(n*m), n为主串长度,m为模式串长度;空间复杂度: O(1);
代码:
const BFmate = (str,sub) => {
let i=0,j=0;
while(i< str.length && j<sub.length) {
if(str[i] === sub[j]) {
i++;
j++;
}else {
i = i-j+1; // 回到 i 的初始位置并前移一位
j = 0; // 回到初始位置
}
}
//跳出循环有两种可能,i=strlen(str)说明已经遍历完主串,匹配失败;j=strlen(sub),说明模式串遍历完成,在主串中成功匹配
if(j===sub.length) {// 字串指针走到最后,匹配结束,完成匹配
return i- sub.length + 1; // 主串位置减去字串位置表示回到珠串匹配成功初始位置
}
//运行到此,为 i==strlen(sub) 的情况,模式匹配失败
return -1;
}
KMP(快速匹配算法)
KMP匹配过程
在暴力匹配过程中,如果主串和模式串某个字符不匹配,将从模式串的第一个字符和主串的下一个字符开始重新匹配,这种算法时间复杂度则是
O(mn);KMP算法的核心是利用匹配失败后的信息,尽量减模式串与主串的匹配次数以达到快速匹配的目的。
示例:字符串 Str1 = “BBC ABCDAB ABCDABCDABDE”,判断里面是否包含另一个字符串 Str2 = “ABCDABD”:
1、首先,用Str1的第一个字符和Str2的第一个字符去比较,不符合,关键词向后移动一位。
2、重复第一步,还是不符合,再后移。
3、一直重复,直到Str1有一个字符与Str2的第一个字符符合为止。
4、接着比较字符串和搜索词的下一个字符,还是符合。
5、遇到Str1有一个字符与Str2对应的字符不符合。
6、这时候想到的是继续遍历Str1的下一个字符,重复第1步。
7、其实这是很不明智的,因为此时”ABCDAB”已经比较过了,没有必要再做重复的工作,一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是”ABCDAB”。
KMP算法的想法是,设法利用这个已知信息,不要把”搜索位置“移回已经比较过的位置,继续把他向后移,这样就提高了效率。
怎么做到把刚刚重复的步骤省略掉?可以对Str2计算出一张《匹配表》,这张表的产生在后面介绍。
8、已知空格与D不匹配时,前面六个字符”ABCDAB”是匹配的。查表可知,最后一个匹配字符B对应的”部分匹配值”为2,因此我们只需要让模式串Str2的下标移动到对应下标为2的位置,也就是C,此时Str1的下标还是保持不变,在空格处,这样就避免了Str1下标回溯到第6步了,这样就大大减少了Str1的比较次数。
9、因为空格与C不匹配,搜索词还要继续往后移。这时已匹配的字符串为”AB”,最后一个匹配字符B对应的”部分匹配值”为0。因此我们只需要让模式串Str2的下标移动到对应下标为0的位置,也就是A,此时Str1的下标还是保持不变。
10、因为空格与A不匹配,并且此时并没有匹配的字符,因此只能继续后移一位。
11、然后逐位比较,直到发现C与D不匹配。
12、因为C与D不匹配,这时已匹配的字符串为”ABCDAB”,最后一个匹配字符B对应的”部分匹配值”为2。因此我们只需要让模式串Str2的下标移动到对应下标为2的位置,也就是C,此时Str1的下标还是保持不变。
13、然后逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。
KMP的部分匹配表
字符串的前缀和后缀
- 前缀:包含首字母但不包含尾字母的所有子串。
- 如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就称B为A的前缀。
- 例如,”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”},我们把所有前缀组成的集合,称为字符串的前缀集合;
- 后缀:包含尾字母但不包含首字母的所有子串。
- 后缀A=SB, 其中S是任意的非空字符串,那就称B为A的后缀
- 例如,”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”},然后把所有后缀组成的集合,称为字符串的后缀集合
KMP的部分匹配表
KMP的部分匹配表:字符串的前缀集合与后缀集合的交集中最长元素的长度。
示例:对于字符串”ababa”,它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”},它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}, 两个集合的交集为{”a”, ”aba”},其中最长的元素为”aba”,长度为3
以模式串“ABCAB”为例,逐步获取该模式串的匹配表:
A:
- 前缀:空;
- 后缀:空;
- 两个集合的交集为空,匹配值为0;
AB:匹配值为0;
- 前缀:{A};
- 后缀:{B};
- 两个集合的交集为空,匹配值为0;
ABC:匹配值为0;
- 前缀:{A}、{AB};
- 后缀:{B}、{BC};
- 两个集合的交集为空,匹配值为0;
ABCA:匹配值为1;
- 前缀:{A}、{AB}、{ABC};
- 后缀:{A}、{CA}、{BCA};
- 两个集合的交集为{A},最长元素长度为1,匹配值为1;
ABCAB:匹配值为2:
- 前缀:{A}、{AB}、{ABC}、{ABCA};
- 后缀:{B}、{AB}、{CAB}、{BCAB};
- 两个集合的交集为{AB},最长元素长度为2,匹配值为2;
因此,“ABCAB” 该模式串的匹配表为
注意:模式串中第一个字符对应的 为 0,这是固定不变的。
部分匹配表算法实现
- 思路:
构建 next 数组,next[j] 表示str[j] 字符前面的字符串中最大的公共前后缀的长度;
KMP 算法永不回退 模式串 的指针
j,而是借助next数组中储存的信息把 指针 移到正确的位置继续匹配;
代码:
function getNext(pattern) {
const next = new Array(pattern.length); // 创建一个用于存储next数组的数组
next[0] = -1; // 初始化next[0]为-1
let i = 0; // i为当前字符的位置
let j = -1; // j为当前字符的最长前缀的后缀的位置
while (i < pattern.length - 1) {
if (j === -1 || pattern[i] === pattern[j]) {
// 当j为-1(即最长前缀的后缀不存在)或当前字符与最长前缀的后缀相等时
i++;
j++;
next[i] = j; // 设置next[i]为j
} else {
j = next[j]; // 更新j为当前字符的最长前缀的后缀的位置
}
}
return next;
}
KMP 算法实现
function kmpSearch(text, pattern) {
const next = getNext(pattern); // 获取模式字符串的next数组
let i = 0; // text的索引
let j = 0; // pattern的索引
while (i < text.length && j < pattern.length) {
if (j === -1 || text[i] === pattern[j]) {
// 当j为-1(即最长前缀的后缀不存在)或当前字符匹配时
i++;
j++;
} else {
j = next[j]; // 更新j为当前字符的最长前缀的后缀的位置
}
}
if (j === pattern.length) {
return i - j; // 返回匹配的起始位置
} else {
return -1; // 未找到匹配
}
}
const text = 'ABABDABACDABABCABAB';
const pattern = 'ABABCABAB';
const index = kmpSearch(text, pattern);
console.log(index); // 输出匹配的起始位置
正则表达式
正则表达式基础:正则表达式 – 教程 | 菜鸟教程 (runoob.com)
使用正则表达式适合做字符串的模式匹配
算法题
密码验证合格程序
实现
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void async function () {
let passwords = []
let res = []
while (line = await readline()) {
passwords.push(line)
}
for (let i = 0; i < passwords.length; i++) {
let pwd = passwords[i]
const flag = validLen(pwd) && !hasEmptyCode(pwd) && validCode(pwd) && !hasRepeatCode(pwd)
res.push(flag ? 'OK' : 'NG')
}
console.log(res.join('\n'))
}()
function validLen(pwd) {
if (pwd.length <= 8)
return false
return true
}
function hasEmptyCode(pwd) {
return /\s/.test(pwd)
}
function validCode(pwd) {
let pats = [/[a-z]+/g, /[A-Z]+/g, /\d+/g, /[^\da-zA-Z]/g]
let trueNnum = 0
for (let i = 0; i < pats.length; i++) {
if (pats[i].test(pwd)) {
trueNnum++
}
}
return (trueNnum >= 3)
}
// 求长度大于3的公共子串
function hasRepeatCode(pwd) {
return /(.{3,}).*\1/g.test(pwd)
}
求字符串是否有重复子串
描述:
重复子串是指一个字符串的子串重复部分,如 021Abc9Abc1 重复子串为 Abc。
解法一:正则匹配
function hasRepeatCode(pwd) {
return /(.{3,}).*\1/g.test(pwd)
}
正则表达式
/(.{3,}).*\1/g匹配字符串中重复出现的、长度至少为3的子串:
(.{3,}):
(和):这两个括号是捕获组,用于捕获匹配的子串,并可以在后面的表达式中通过反斜杠和数字(如\1)来引用。.:这个字符是一个通配符,匹配除了换行符之外的任何字符。{3,}:这是一个量词,表示前面的元素(在这里是.)必须出现至少3次。因此,这个捕获组会匹配任何长度至少为3的连续字符序列。.\*:
.:同样是一个通配符,匹配除了换行符之外的任何字符。*:这是一个量词,表示前面的元素(在这里是.)可以出现0次或多次。因此,.*会匹配任何数量的连续字符(包括0个字符),直到它遇到下一个要匹配的元素或字符串的末尾。\1:
- 这是一个反向引用,它引用了前面第一个捕获组(即
(.{3,}))捕获的内容。这意味着,正则表达式会查找与第一个捕获组捕获的子串完全相同的子串。/g:
- 这是一个全局标志,表示这个正则表达式应该在整个字符串中查找所有匹配的子串,而不仅仅是第一个。
现在,让我们看一个例子来更好地理解这个正则表达式的工作原理:
对于字符串 "abcabcxyz",这个正则表达式会匹配 "abcabc",因为 "abc" 是第一个捕获组捕获的子串,并且它在字符串中再次出现。但是,它不会匹配 "xyz" 或 "abcxyz",因为 "xyz" 不与第一个捕获组捕获的内容匹配,而 "abcxyz" 中的 "abc" 后面没有紧接着再次出现。
注意:这个正则表达式可能会产生一些非预期的匹配,特别是当字符串中包含多个相同且长度大于或等于3的子串时。例如,在字符串 "abcabcabc" 中,它会匹配整个 "abcabcabc",而不仅仅是第一个 "abcabc" 重复。如果你只想匹配最小的重复子串,那么你可能需要使用更复杂的正则表达式或算法。
算法题
字符串基础题目
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 0125 | 验证回文串 | 双指针、字符串 | 简单 |
| 0005 | 最长回文子串 | 字符串、动态规划 | 中等 |
| 0003 | 无重复字符的最长子串 | 哈希表、字符串、滑动窗口 | 中等 |
| 0344 | 反转字符串 | 双指针、字符串 | 简单 |
| 0557 | 反转字符串中的单词 III | 双指针、字符串 | 简单 |
| 0049 | 字母异位词分组 | 数组、哈希表、字符串、排序 | 中等 |
| 0415 | 字符串相加 | 数学、字符串、模拟 | 简单 |
| 0151 | 反转字符串中的单词 | 双指针、字符串 | 中等 |
| 0043 | 字符串相乘 | 数学、字符串、模拟 | 中等 |
| 0014 | 最长公共前缀 | 字典树、字符串 | 简单 |
单模式串匹配题目
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 0028 | 找出字符串中第一个匹配项的下标 | 双指针、字符串、字符串匹配 | 中等 |
| 0459 | 重复的子字符串 | 字符串、字符串匹配 | 简单 |
| 0686 | 重复叠加字符串匹配 | 字符串、字符串匹配 | 中等 |
| 1668 | 最大重复子字符串 | 字符串、字符串匹配 | 简单 |
| 0796 | 旋转字符串 | 字符串、字符串匹配 | 简单 |
| 1408 | 数组中的字符串匹配 | 数组、字符串、字符串匹配 | 简单 |
| 2156 | 查找给定哈希值的子串 | 字符串、滑动窗口、哈希函数、滚动哈希 | 困难 |
字典树题目
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 0208 | 实现 Trie (前缀树) | 设计、字典树、哈希表、字符串 | 中等 |
| 0677 | 键值映射 | 设计、字典树、哈希表、字符串 | 中等 |
| 0648 | 单词替换 | 字典树、数组、哈希表、字符串 | 中等 |
| 0642 | 设计搜索自动补全系统 | 设计、字典树、字符串、数据流 | 困难 |
| 0211 | 添加与搜索单词 - 数据结构设计 | 深度优先搜索、设计、字典树、字符串 | 中等 |
| 0421 | 数组中两个数的最大异或值 | 位运算、字典树、数组、哈希表 | 中等 |
| 0212 | 单词搜索 II | 字典树、数组、字符串、回溯、矩阵 | 困难 |
| 0425 | 单词方块 | 字典树、数组、字符串、回溯 | 困难 |
| 0336 | 回文对 | 字典树、数组、哈希表、字符串 | 困难 |
| 1023 | 驼峰式匹配 | 字典树、双指针、字符串、字符串匹配 | 中等 |
| 0676 | 实现一个魔法字典 | 设计、字典树、哈希表、字符串 | 中等 |
| 0440 | 字典序的第K小数字 | 字典树 | 困难 |
获取字单词中英文字母的下一个字符
思路
- 遍历输入字符串的每个字符。
- 检查当前字符是否是英文字母(在ASCII码表中,英文字母的范围大致是65-90(大写)和97-122(小写))。
- 如果是英文字母,则通过增加其Unicode码点值来获取下一个字符。注意处理'z'和'Z'的特殊情况。
- 如果不是英文字母,则跳过该字符并继续遍历。
- 将所有处理后的字符连接成一个新的字符串。
function getNextCharInWord(word) {
let result = '';
for (let i = 0; i < word.length; i++) {
// charCodeAt() 返回指定索引处字符的Unicode编码
const charCode = word.charCodeAt(i);
// 检查是否为英文字母,大写: 65-90 ,小写:97-122
if ((charCode >= 65 && charCode <= 90) || (charCode >= 97 && charCode <= 122)) {
if (charCode === 122 || charCode === 90) { // 'z' 或 'Z' 的情况
// 这里你可以选择将下一个字符定义为其他字符,比如 'a' 或 'A',或者一个特殊字符
result += (charCode === 122) ? 'a' : 'A';
} else {
//fromCharCode 返回由指定的 UTF-16 码元序列创建的字符串
result += String.fromCharCode(charCode + 1); // 增加Unicode码点值获取下一个字符
}
} else {
result += word[i]; // 非英文字母字符保持不变
}
}
return result;
}
// 示例用法
const word = 'Hello, World!';
console.log(getNextCharInWord(word)); // 输出:'Ifmmp, Xpsme!'(注意这里的实现将'z'和'Z'的下一个字符定义为'a'和'A')
反转字符串
题目
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
不要给另外的数组分配额外的空间,你必须**原地修改输入数组**、使用 O(1) 的额外空间解决这一问题。
示例 1:
输入:s = ["h","e","l","l","o"]
输出:["o","l","l","e","h"]
示例 2:
输入:s = ["H","a","n","n","a","h"]
输出:["h","a","n","n","a","H"]
解法:双指针
- 使用两个指针分别指向头部和尾部,并向中间靠拢遍历;
- 指针指向位置进行替换;
- 当两个指针位置相等时结束。
function reverseString(s: string[]): void {
let left = 0
let right = s.length - 1
while (left < right) {
let temp = s[left]
s[left] = s[right]
s[right] = temp
left++
right--
}
};
最长公共前缀
题目
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串
""。示例:
输入:strs = ["flower","flow","flight"] 输出:"fl"输入:strs = ["dog","racecar","car"] 输出:"" 解释:输入不存在公共前缀。提示:
1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i]仅由小写英文字母组成
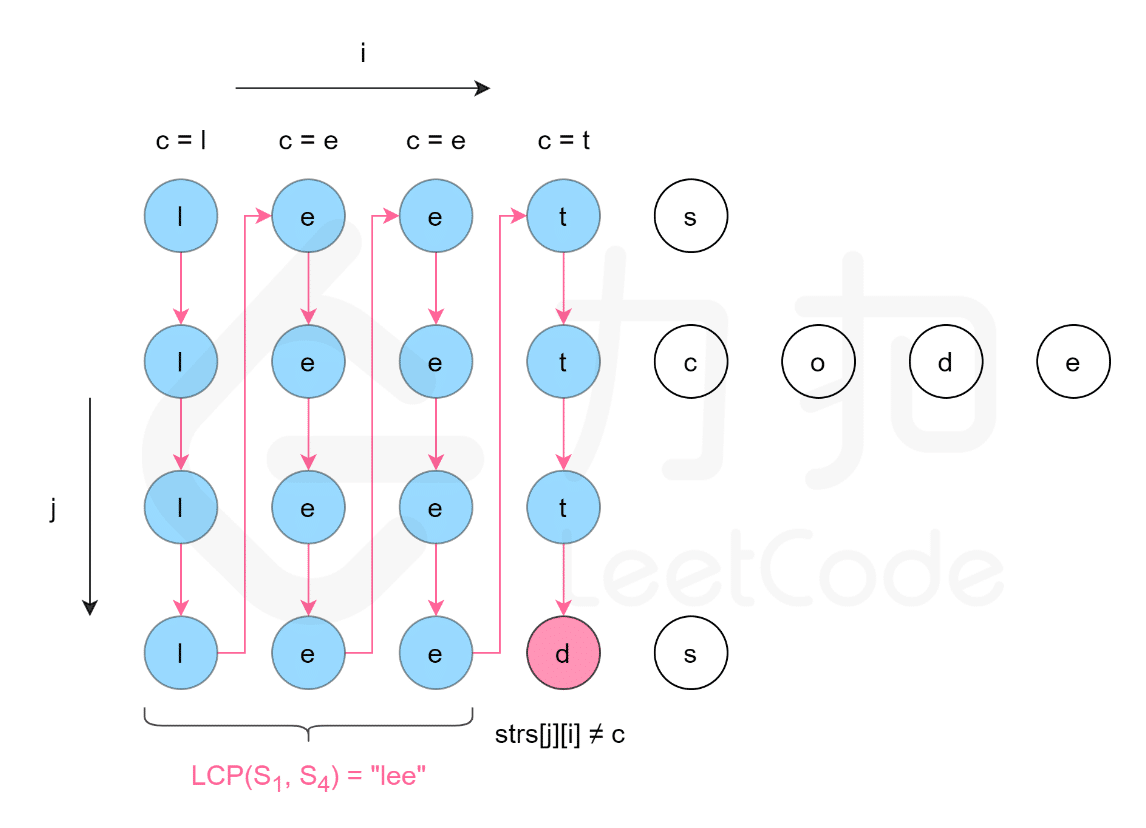
解法一:纵向扫描,逐个单词匹配
把字符串数组看作一个二维数组
设定指针 i 指向数组元素,指针 j 指向字符串;
取数组中第一个字符串的每个字符作为单词 word;
遍历数组,比较数组中每个字符串对应位置的单词是否等于 word:
- 相等,继续查找下一个字符串的对应位置单词
- 不相等,退出循环
数组遍历完成后,执行以下操作:
- 重置数组下标,从数组第二个元素开始遍历;
- 字符串单词指针后移一位;
- 拼接单词和公共字符串
- 继续取第一个字符串的每个字符作为单词 word;
注意:注意边界条件判断;
复杂度:
- 时间复杂度:O(mn),其中 m是字符串数组中的字符串的平均长度,n 是字符串的数量。最坏情况下,字符串数组中的每个字符串的每个字符都会被比较一次。
- 空间复杂度:O(1)。使用的额外空间复杂度为常数。
代码
/**
* @param {string[]} strs
* @return {string}
*/
var longestCommonPrefix = function(strs) {
if(strs.length === 0) return ""; // 边界条件:strs为空,返回空
if(strs.length === 1) return strs[0];// 边界条件:strs长度为1,返回唯一的字符串
let subStr = "";
let i=1,j = 0;
let word = '';
let flag = true;
while(flag){
if(i === strs.length) {
i=1;
j++;
subStr += word;
}
word = strs[0][j];
if(!word) {// 边界条件:空字符串时,退出循环
flag = false
}
if(strs[i][j] === word) {
i++;
}else {
flag = false
}
}
return subStr;
};
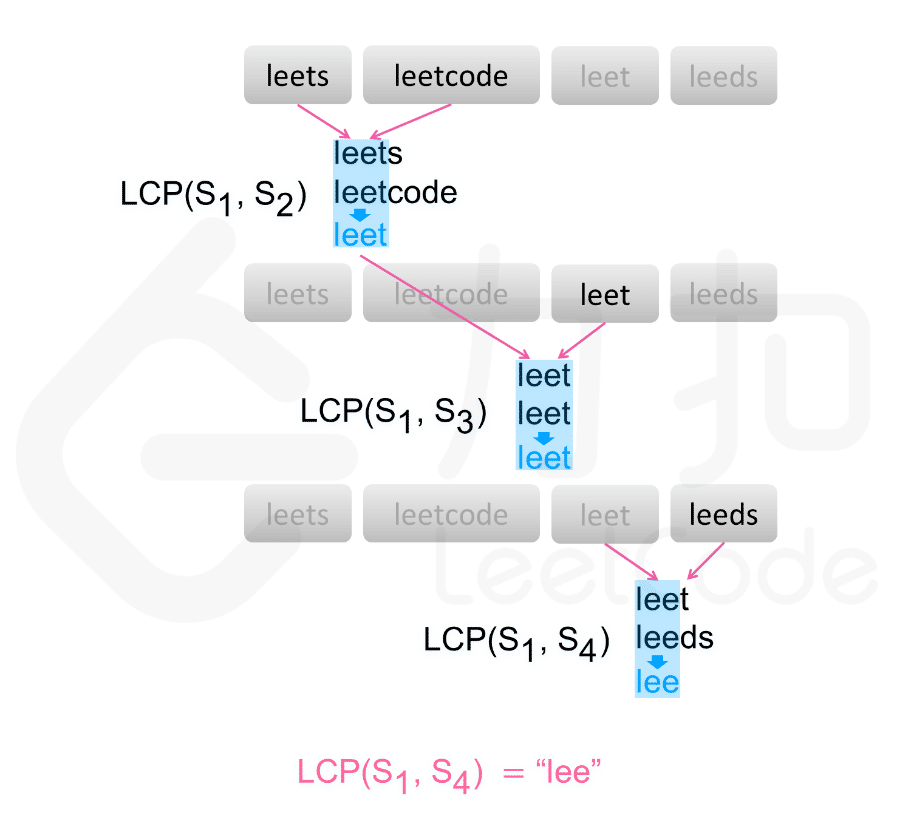
解法二:横向扫描,求解相邻字符串的最长公共前缀
假设第一个字符串为最长公共前缀串 prefix;
依次遍历字符串数组中的每个字符串,对于每个遍历到的字符串:
- 获取当前字符串 strs[i] 和最长公共前缀串 prefix 的 最长公共前缀串;
- 更新最长公共前缀;
当遍历完所有的字符串以后,即可得到字符串数组中的最长公共前缀
复杂度:
- 时间复杂度:O(mn),其中 m是字符串数组中的字符串的平均长度,n 是字符串的数量。最坏情况下,字符串数组中的每个字符串的每个字符都会被比较一次。
- 空间复杂度:O(1)。使用的额外空间复杂度为常数。
代码:
var longestCommonPrefix = function(strs) {
if(!strs || strs.length ===0) return "";
let prefix = strs[0];
for(let i=1; i< strs.length; i++) {
prefix = getLongestCommonPrefix(prefix,strs[i]);
if(!prefix) break;
}
return prefix;
}
var getLongestCommonPrefix = function(prefix, str) {
let len = Math.min(prefix.length,str.length);
let i=0;
while(i<len) {
if(prefix[i]===str[i]){
i++;
}else {
break;
}
}
return prefix.slice(0,i);
}
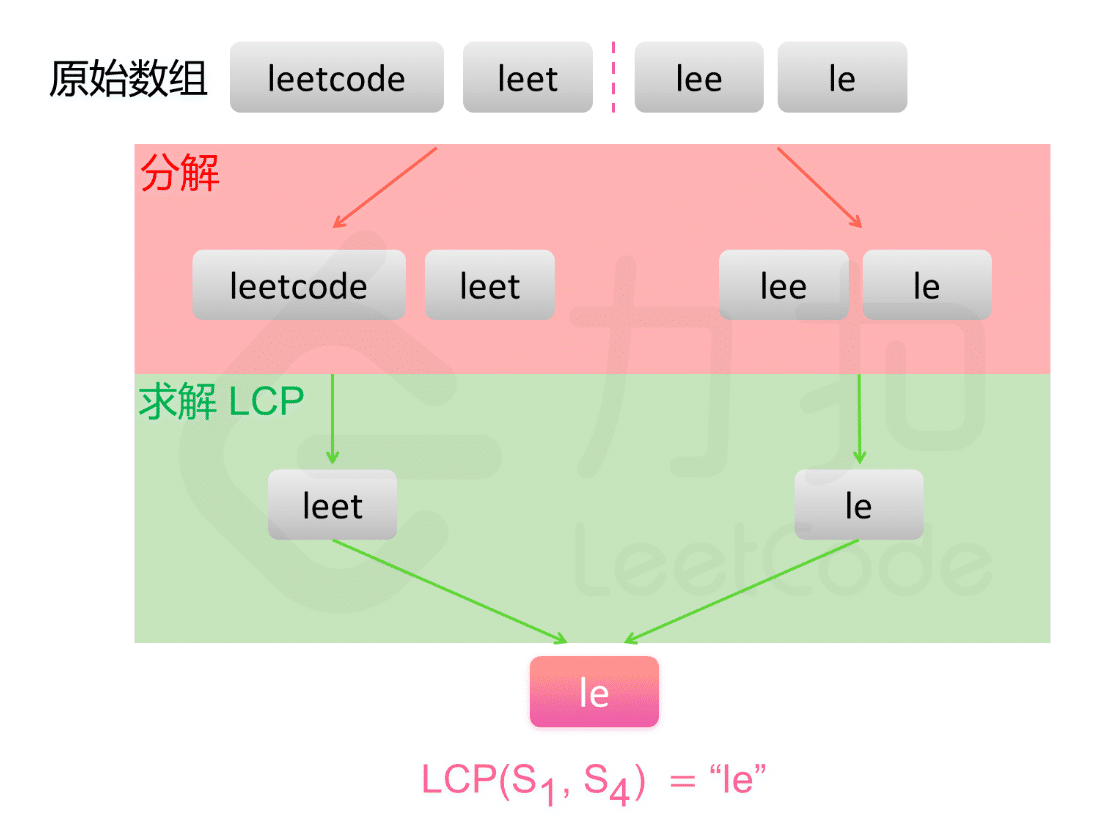
解法三:分治
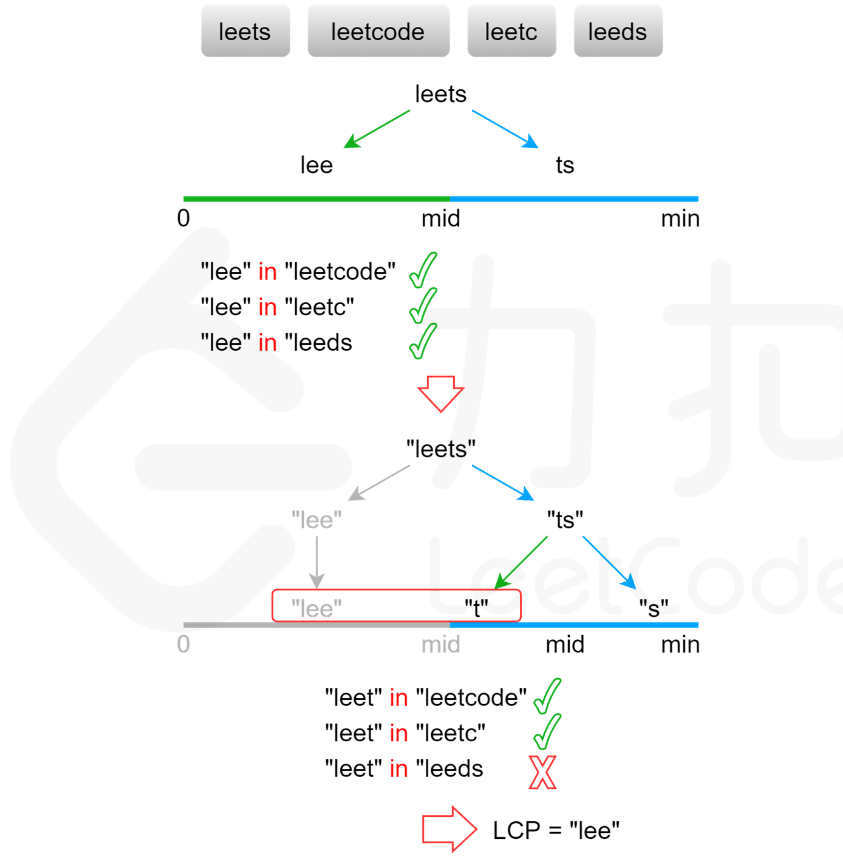
对于问题 LCP(Si⋯Sj),可以分解成两个子问题 LCP(Si…Smid)与 LCP(Smid+1…Sj),其中 mid=i+j2。
递归对两个子问题分别求解,然后对两个子问题的解计算最长公共前缀,即为原问题的解。
代码
var longestCommonPrefix = function(strs) {
if(!strs || strs.length==0) return "";
return splitArray(strs,0,strs.length-1);
}
// 拆分数组
var splitArray = function(strs,start,end) {
if(start === end) {
return strs[start];
}else {
// 注意中间位置要取整
let mid = Math.floor((end - start)/2) + start;
let left = splitArray(strs,start,mid); // 拆分左侧数组
let rifht = splitArray(strs,mid+1,end);// 拆分右侧数组
return commonPrefix(left,rifht); // 求左右数组字符串最大公共前缀
}
}
var commonPrefix = function(left,right) {
let len = Math.min(left.length,right.length);
let i=0;
while(left[i] === right[i] && i< len) {
i++;
}
return left.slice(0,i);
}
解法四:二分查找
最长公共前缀的长度不会超过字符串数组中的最短字符串的长度。
用 minLength表示字符串数组中的最短字符串的长度,则可以在[0,minLength] 的范围内在第一个字符串上通过二分查找,得到最长公共前缀的长度,最长公共前缀的长度就是查找到的位置 i.
每次取查找范围的中间值 mid,判断每个字符串的长度为 mid 的前缀是否相同:
- 如果相同则最长公共前缀的长度一定大于或等于 mid;
- 如果不相同则最长公共前缀的长度一定小于 mid;
- 通过上述方式将查找范围缩小一半,直到得到最长公共前缀的长度。
代码
var longestCommonPrefix = function(strs) {
if(!strs || strs.length==0) return "";
let minLength = Infinity;
// 查找最小长度的字符串长度
for(let i=0;i<strs.length; i++) {
minLength = Math.min(minLength,strs[i].length);
}
// 取第一个字符串,从 [0,minLength] 区间查找最长公共前缀的位置
let low = 0, height = minLength;
while(low<height) {
// 取字符串中间位置,二分查找最小长度的字符串长度位置
let mid = Math.floor((height-low+1)/2) + low;
if(isCommonPrefix(strs,mid)) { // [0,mid] 是公共前缀串,则说明最长公共前缀的位置在 [mid,minLength]
low = mid;
}else {
height = mid-1;
}
}
return strs[0].slice(0,low); // 返回第一个字符串截取的最长公共前缀的位置子串
}
var isCommonPrefix = function(strs,pos) {
let prefixStr = strs[0].slice(0,pos);//截取第一个字符串的 [0,pos]位置子串,判断子串是否为公共前缀(注意:不是最长公共前缀)
// 遍历其他字符串,判断是否 prefixStr 是否为前缀串
for(let i=1; i< strs.length; i++) {
let subStr = strs[i].slice(0,pos);
if(prefixStr != subStr) {
return false
}
}
return true
}
最长回文子串
题目
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd" 输出:"bb"提示:
1 <= s.length <= 1000 s 仅由数字和英文字母组成
解法一:动态规划
思路与算法
对于一个子串而言,如果它是回文串,并且长度大于 2 ,那么将它首尾的两个字母去除之后,它仍然是个回文串。
例如对于字符串 “ababa” 如果我们已经知道 “bab” 是回文串,那么 “ababa” 一定是回文串,这是因为它的首尾两个字母都是 “a”
根据这样的思路,我们就可以用动态规划的方法解决本题:
- 划分阶段:
按照回文字符串长度、子串回文串划分阶段;
- 定义状态:
我们用 P(i,j) 表示字符串 s 的第 i 到 j 个字母组成的串是否为回文串(下文表示成 s[i:j] ):

这里的「其它情况」包含两种可能性:
s[i,j]本身不是一个回文串;i>j,此时s[i,j]本身不合法。
- 定义状态转移方程:
那么我们就可以写出动态规划的状态转移方程:
P(i,j) = P(i+1,j−1 ) ∧ (S[i] == S[j])
也就是说,只有 s[i+1:j−1] 是回文串,并且 s 的第 i 和 j 个字母相同时,s[i:j] 才会是回文串。
- 初始条件:
上文的所有讨论是建立在子串长度大于 2 的前提之上的,我们还需要考虑动态规划中的边界条件,即子串的长度为 1 或 2 。
- 对于长度为 1 的子串,它显然是个回文串;
- 对于长度为 2 的子串,只要它的两个字母相同,它就是一个回文串。
因此我们就可以写出动态规划的边界条件:
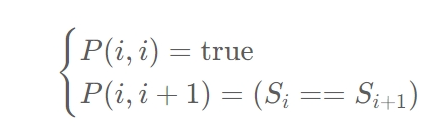
- 最终结果:
根据这个思路,我们就可以完成动态规划了,最终的答案即为所有 P(i,j)=true 中 j−i+1 (即子串长度)的最大值。
注意:在状态转移方程中,我们是从长度较短的字符串向长度较长的字符串进行转移的,因此一定要注意动态规划的循环顺序。
public longestPalindrome(s: string): string {
const len = s.length;
if (len < 2) {
// 如果字符串长度小于2,则它本身就是最长的回文串
return s;
}
let maxLen = 1; // 最长回文串的长度
let begin = 0; // 最长回文串的起始位置
// dp[i][j] 表示 s 的子串 s[i...j] 是否是回文串
const dp: boolean[][] = new Array(len).fill(null).map(() => new Array(len).fill(false));
// 初始化:所有长度为 1 的子串都是回文串 ,从 [i,i] 的长度为 1
for (let i = 0; i < len; i++) {
dp[i][i] = true;
}
const charArray = s.split(''); // 将字符串转换为字符数组
// 递推开始
// 先枚举子串长度,枚举所有可能的子串长度
for (let L = 2; L <= len; L++) {
// 枚举左边界位置
for (let i = 0; i < len; i++) {
// 由 L 和 i 可以确定右边界,根据 L = j-i+1 推导出 j
const j = i + L - 1;
// 如果右边界越界,则退出当前循环
if (j >= len) {
break;
}
// 判断 s[i...j] 是否是回文串
// 左右边界字符不相等,则不是回文串
if (charArray[i] !== charArray[j]) {
dp[i][j] = false;
} else { // 左右边界字符相等
// 如果子串长度小于3,则一定是回文串
// 否则需要判断去掉首尾字符的子串是否是回文串
if (L < 3) {
dp[i][j] = true;
} else { // 根据动态规划方程,当前左右边界相等时候,是否为回文串取决于上一个字串
dp[i][j] = dp[i + 1][j - 1];
}
}
// 如果当前子串是回文串,并且长度比之前记录的最长回文串还要长
// 则更新最长回文串的长度和起始位置
if (dp[i][j] && L > maxLen) {
maxLen = L;
begin = i;
}
}
}
// 返回最长回文串
return s.substring(begin, begin + maxLen);
}
解法二:中心扩展法
思路
从每一个位置出发,向两边扩散即可。遇到不是回文的时候结束。
举个例子,str=acdbbdaa 我们需要寻找从第一个 b(位置为 3)出发最长回文串为多少。怎么寻找?
- 首先往左寻找与当期位置相同的字符,直到遇到不相等为止。
- 然后往右寻找与当期位置相同的字符,直到遇到不相等为止。
- 最后左右双向扩散,直到左和右不相等
位置中心有两种情况:
一种是回文子串长度为奇数(如aba,中心是b)
另一种回文子串长度为偶数(如abba,中心是b,b)
循环遍历字符串 对取到的每个值 都假设他可能成为最后的中心进行判断
代码
/**
* @param {string} s
* @return {string}
*/
var longestPalindrome = function(s) {
if (s.length<2){
return s;
}
let sub = '';
for (let i = 0; i < s.length; i++) {
// 回文子串长度是奇数
expandAroundCenter(i, i);
// 回文子串长度是偶数
expandAroundCenter(i, i + 1);
}
function expandAroundCenter(left, right) {
while (left >= 0 && right < s.length && s[left] == s[right]) {
left--;
right++;
}
// 注意此处m,n的值循环完后 是恰好不满足循环条件的时刻
// 此时m到n的距离为n-m+1,但是mn两个边界不能取 所以应该取m+1到n-1的区间 长度是n-m-1
// 如果此时回文串比上一个回文串长度大,取较长的回文串
if (right - left - 1 > sub.length) {
// slice也要取[m+1,n-1]这个区间
sub = s.slice(m + 1, n);
}
}
return sub;
};
翻转字符串里的单词
题目
给你一个字符串 s ,请你反转字符串中 单词的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
输入:s = "the sky is blue" 输出:"blue is sky the"示例 2:
输入:s = " hello world " 输出:"world hello" 解释:反转后的字符串中不能存在前导空格和尾随空格。示例 3:
输入:s = "a good example" 输出:"example good a" 解释:如果两个单词间有多余的空格,反转后的字符串需要将单词间的空格减少到仅有一个。提示:
1 <= s.length <= 104 s 包含英文大小写字母、数字和空格 ' ' s 中 至少存在一个 单词
进阶:如果字符串在你使用的编程语言中是一种可变数据类型,请尝试使用 O(1) 额外空间复杂度的 原地 解法。
解法一:使用栈保存单词顺序
- 使用栈保存整个单词顺序,定义单词截取起始点 start;
- 遍历字符串,查找空格字符:
- 遇到空格字符,以空格字符为分割点,截取 start 到空格字符前一个位置字符串入栈,start 记录空格字符位置;
- 遍历结束,将栈所有单词按顺序出栈,并使用空格拼接;
- 注意:
- 遍历到字符串末尾时候,需要判断末尾字符串,截取位置为字符串长度;
- 入栈前需要将字符串去除首尾空格
- 时间复杂度:O(n),空间复杂度:O(n)
/**
* @param {string} s
* @return {string}
*/
var reverseWords = function(s) {
let str = s.trim();
let stack = [];
let start = 0;
let flipStr = '';
for(let i=0; i< str.length; i++) {
if(str[i]== ' ' || i==str.length-1) {
//遍历到字符串末尾时候,需要判断末尾字符串,截取位置为字符串长度;
let end = i==str.length-1? str.length: i
let subStr = str.slice(start,end).trim();//入栈前需要将字符串去除首尾空格
if(subStr) {
stack.push(subStr);
}
start = i;// 记录下一个起始位置
}
}
while(stack.length!==0) {
flipStr += stack.pop() + ' '
}
return flipStr.trim();
};
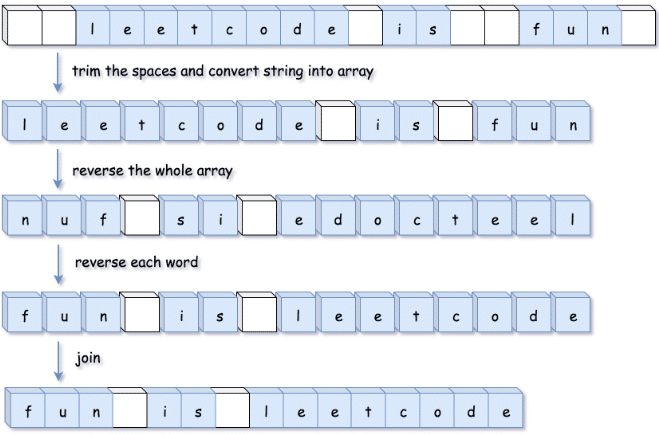
解法二:整体翻转后单个单词翻转
- 去除字符串首尾空格;
- 字符串整体翻转;
- 遍历字符串再单个单词翻转;
时间复杂度:O(n),空间复杂度O(1)
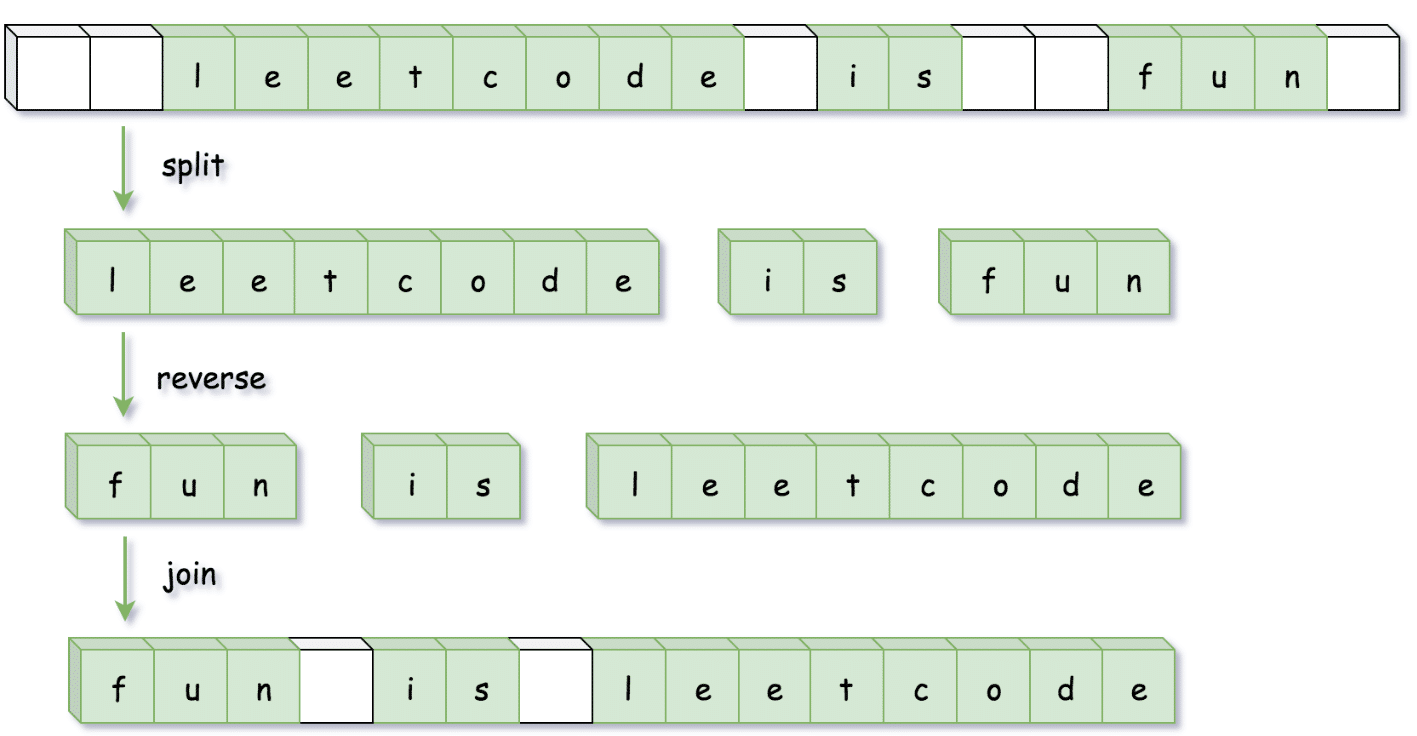
解法三:使用语言特性
很多语言对字符串提供了 split(拆分),reverse(翻转)和 join(连接)等方法,因此我们可以简单的调用内置的 API 完成操作:
使用 split 将字符串按空格分割成字符串数组;
使用 reverse 将字符串数组进行反转;
使用 join 方法将字符串数组拼成一个字符串。
复杂度分析
时间复杂度:O(n),其中 n为输入字符串的长度。
空间复杂度:O(n),用来存储字符串分割之后的结果。
var reverseWords = function(s) {
return s.trim().split(/\s+/).reverse().join(' ');
};