队列

SewenAbout 14 min

队列

定义和特点

队列（Queue）：一种线性表数据结构，是一种只允许在表的一端进行插入操作，而在表的另一端进行删除操作的线性表。

队列是一种线性数据结构，具有先进先出（FIFO）的特性。
可以类比为排队买票，先来的人先被服务。
可以使用数组的push()和shift()方法来实现。

基本操作

入队（Enqueue）：将元素放入队列的末尾。
出队（Dequeue）：从队列的头部移除元素，并返回移除的元素。
获取队头元素（Front）：返回队列头部的元素，并不移除该元素。
判断队列是否为空（isEmpty）：检查队列是否为空。

class Queue {  
    // 初始化空队列  
    constructor(size = 100) {  
        this.size = size;  
        this.queue = new Array(size).fill(null); // 初始化队列数组  
        this.front = -1;  
        this.rear = -1;  
    }  
  
    // 判断队列是否为空  
    isEmpty() {  
        return this.front === this.rear;  
    }  
  
    // 判断队列是否已满  
    isFull() {  
        return (this.rear + 1) % this.size === this.front; // 使用取模操作来处理循环队列  
    }  
  
    // 入队操作  
    enqueue(value) {  
        if (this.isFull()) {  
            throw new Error('Queue is full');  
        } else {  
            this.rear = (this.rear + 1) % this.size; // 更新队尾指针，使用取模操作来处理循环  
            this.queue[this.rear] = value;  
        }  
    }  
  
    // 出队操作  
    dequeue() {  
        if (this.isEmpty()) {  
            throw new Error('Queue is empty');  
        } else {  
            let value = this.queue[this.front + 1]; // 注意JavaScript中数组索引从0开始  
            this.front = (this.front + 1) % this.size; // 更新队头指针，使用取模操作来处理循环  
            return value;  
        }  
    }  
  
    // 获取队头元素  
    frontValue() {  
        if (this.isEmpty()) {  
            throw new Error('Queue is empty');  
        } else {  
            return this.queue[(this.front + 1) % this.size]; // 注意JavaScript中数组索引从0开始，并使用取模操作  
        }  
    }  
  
    // 获取队尾元素  
    rearValue() {  
        if (this.isEmpty()) {  
            throw new Error('Queue is empty');  
        } else {  
            return this.queue[this.rear];  
        }  
    }  
}  
  
// 使用示例  
let q = new Queue(5);  
q.enqueue(1);  
q.enqueue(2);  
console.log(q.frontValue()); // 输出：1  
console.log(q.rearValue()); // 输出：2  
q.dequeue();  
console.log(q.frontValue()); // 输出：2

优先队列

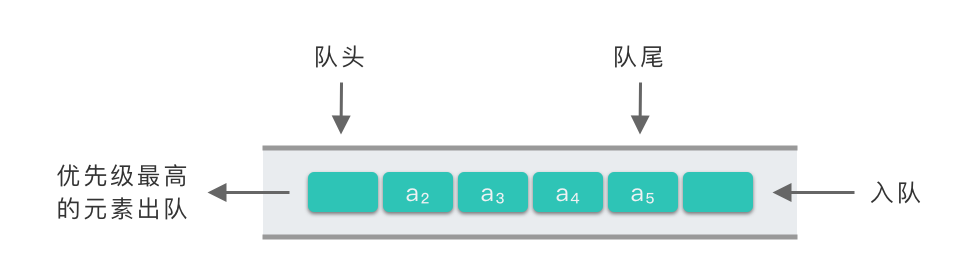
优先队列（Priority Queue）：一种特殊的队列。在优先队列中，元素被赋予优先级，当访问队列元素时，具有最高优先级的元素最先删除。
优先队列与普通队列最大的不同点在于 出队顺序。
优先队列的出队顺序跟入队顺序无关，优先队列是按照元素的优先级来决定出队顺序的：
优先级高的元素优先出队，优先级低的元素后出队。
优先队列符合 「最高级先出（First in, Largest out）」 的规则。

优先队列的适用场景

数据压缩：赫夫曼编码算法；
最短路径算法：Dijkstra 算法；
最小生成树算法：Prim 算法；
任务调度器：根据优先级执行系统任务；
事件驱动仿真：顾客排队算法；
排序问题：查找第 k 个最小元素。

优先队列的实现方式

优先队列所涉及的基本操作跟普通队列差不多，主要是 「入队操作」 和 「出队操作」。

而优先队列的实现方式也有很多种，除了使用「数组（顺序存储）实现」与「链表（链式存储）实现」之外，我们最常用的是使用 **「二叉堆结构实现」**优先队列。以下是三种方案的介绍和总结。

数组（顺序存储）实现优先队列：入队操作直接插入到数组队尾，时间复杂度为 𝑂(1)。出队操作需要遍历整个数组，找到优先级最高的元素，返回并删除该元素，时间复杂度为 𝑂(𝑛)。
链表（链式存储）实现优先队列：链表中的元素按照优先级排序，入队操作需要为待插入元素创建节点，并在链表中找到合适的插入位置，时间复杂度为 𝑂(𝑛)。出队操作直接返回链表队头元素，并删除队头元素，时间复杂度为 𝑂(1)。
二叉堆结构实现优先队列：构建一个二叉堆结构，二叉堆按照优先级进行排序。入队操作就是将元素插入到二叉堆中合适位置，时间复杂度为 𝑂(log2⁡𝑛)。出队操作则返回二叉堆中优先级最大节点并删除，时间复杂度也是 𝑂(log⁡𝑛)。

下面是三种结构实现的优先队列入队操作和出队操作的时间复杂度总结。

	入队操作时间复杂度	出队操作（取出优先级最高的元素）时间复杂度
堆	𝑂(log⁡𝑛)	𝑂(log⁡𝑛)
数组	𝑂(1)	𝑂(𝑛)
链表	𝑂(𝑛)	𝑂(1)

从上面的表格可以看出，使用「二叉堆」这种数据结构来实现优先队列是比较高效的。下面我们来讲解一下二叉堆实现的优先队列。

二叉堆实现的优先队列

二叉堆实现的优先队列与二叉堆相同，详细知识参考二叉堆：堆 | Sewen 博客 (sewar-x.github.io)

通过手写二叉堆的方式实现优先队列。主要实现了以下五种方法：

heapAdjust：将完全二叉树调整为二叉堆。
heapify：将数组构建为二叉堆方法（初始堆建立方法）。
heappush：向堆中添加元素，也是优先队列的入队操作。
heappop：删除堆顶元素，也是优先队列的出队操作，弹出优先队列中优先级最高的元素。
heapSort：堆排序。

class Heapq {
    // 堆调整方法：调整为大顶堆
    heapAdjust(nums: number[], index: number, end: number): void {
        let left = index * 2 + 1;// 当前节点左子节点
        let right = left + 1; // 右子节点
        while (left <= end) {
            // 当前节点为非叶子结点
            let max_index = index;
            if (nums[left] > nums[max_index]) {
                max_index = left;
            }
            if (right <= end && nums[right] > nums[max_index]) {
                max_index = right;
            }
            if (index === max_index) {
                // 如果不用交换，则说明已经交换结束
                break;
            }
            let temp = nums[index];
            nums[index] = nums[max_index];
            nums[max_index] = temp;
            // 继续调整子树
            index = max_index;
            left = index * 2 + 1;
            right = left + 1;
        }
    }

    // 将数组构建为二叉堆
    heapify(nums: number[]): void {
        let size = nums.length;
        // (size - 2) / 2 是最后一个非叶节点，叶节点不用调整，从最后一个非叶子节点开始调整
        for (let i = (size - 2) >> 1; i >= 0; i--) {
            // 调用调整堆函数
            this.heapAdjust(nums, i, size - 1);
        }
    }

    // 入队操作
    heappush(nums: number[], value: number): void {
        nums.push(value);
        let size = nums.length;
        let i = size - 1;
        // 寻找插入位置
        while ((i - 1) >> 1 >= 0) {
            let cur_root = (i - 1) >> 1;
            // value 小于当前根节点，则插入到当前位置
            if (nums[cur_root] > value) {
                break;
            }
            // 继续向上查找
            nums[i] = nums[cur_root];
            i = cur_root;
        }
        // 找到插入位置或者到达根位置，将其插入
        nums[i] = value;
    }

    // 出队操作
    heappop(nums: number[]): number {
        let size = nums.length;
        let top = nums[0];
        nums[0] = nums[size - 1];
        nums.pop();
        if (size > 0) {
            this.heapAdjust(nums, 0, size - 2);
        }
        return top;
    }

    // 升序堆排序
    heapSort(nums: number[]): number[] {
        this.heapify(nums);
        let size = nums.length;
        for (let i = 0; i < size; i++) {
            nums[0] = nums[size - i - 1];
            nums[size - i - 1] = top;
            this.heapAdjust(nums, 0, size - i - 2);
        }
        return nums;
    }
}

// 使用示例
const heap = new Heapq();
const nums = [3, 2, 5, 1, 7];
console.log(heap.heapSort(nums)); // 输出排序后的数组

算法题

题号	标题	标签	难度
0622	设计循环队列	设计、队列、数组、链表	中等
0346	数据流中的移动平均值	设计、队列、数组、数据流	简单
0225	用队列实现栈	栈、设计、队列	简单

优先队列

题号	标题	标签	难度
0703	数据流中的第 K 大元素	树、设计、二叉搜索树、二叉树、数据流、堆（优先队列）	简单
0347	前 K 个高频元素	数组、哈希表、分治、桶排序、计数、快速选择、排序、堆（优先队列）	中等
0451	根据字符出现频率排序	哈希表、字符串、桶排序、计数、排序、堆（优先队列）	中等
0973	最接近原点的 K 个点	几何、数组、数学、分治、快速选择、排序、堆（优先队列）	中等
1296	划分数组为连续数字的集合	贪心、数组、哈希表、排序	中等
0239	滑动窗口最大值	队列、数组、滑动窗口、单调队列、堆（优先队列）	困难
0295	数据流的中位数	设计、双指针、数据流、排序、堆（优先队列）	困难
0023	合并 K 个升序链表	链表、分治、堆（优先队列）、归并排序	困难
0218	天际线问题	树状数组、线段树、数组、分治、有序集合、扫描线、堆（优先队列）	困难

滑动窗口最大值 (双端队列)（较难）

题目：

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口 k 内的数字。滑动窗口每次只向右移动一位。返回滑动窗口最大值。

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
1 [3  -1  -3] 5  3  6  7       3
1  3 [-1  -3  5] 3  6  7       5
1  3  -1 [-3  5  3] 6  7       5
1  3  -1  -3 [5  3  6] 7       6
1  3  -1  -3  5 [3  6  7]      7

解法一：优先队列

初始的时候将前 𝑘 个元素加入优先队列的二叉堆中:
- 存入优先队列的是数组值与索引构成的元组。
- 优先队列将数组值作为优先级。
然后滑动窗口从第 𝑘 个元素开始遍历，将当前数组值和索引的元组插入到二叉堆中。
当二叉堆堆顶元素的索引已经不在滑动窗口的范围中时，即 𝑞[0][1]≤𝑖−𝑘 时，不断删除堆顶元素，直到最大值元素的索引在滑动窗口的范围中。
将最大值加入到答案数组中，继续向右滑动。
滑动结束时，输出答案数组。

解法二：双端队列

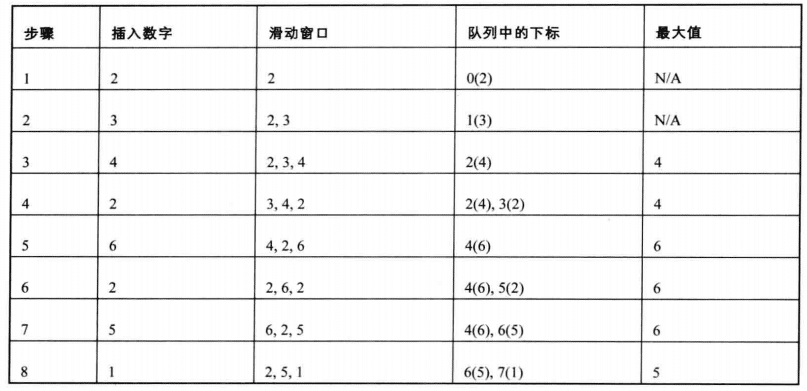
创建一个双向队列（deque）来保存滑动窗口中的元素索引：
- 队列会按照元素大小的降序排列，即队首元素为当前滑动窗口的最大值。
- (注意：队列保存的是滑动窗口的元素索引，但是队列内索引对应元素是降序排序的)
遍历数组 nums，对于每个元素 nums[i]：
- 在插入元素之前，首先检查队首元素是否已经超出滑动窗口的范围（索引范围超过 i-k）。
- 如果队首元素过期，则从队列中删除它，保证队列中的元素都在滑动窗口范围内。
- 然后，将当前元素 nums[i] 与队列中的元素进行比较：
  - 从队列的尾部开始，如果尾部元素小于等于当前元素 nums[i]，则将尾部元素从队列中移除。重复此过程直到队列为空或者队列的尾部元素大于当前元素。
  - 将当前元素的索引插入到队列的尾部。
- 检查当前索引 i 是否已经达到滑动窗口的大小 k。如果是，则滑动窗口形成，此时队首元素即为当前窗口的最大值。
将滑动窗口的最大值保存在结果数组中。
返回结果数组。

时间复杂度：O(n)

空间复杂度：O(n)

使用优先队列也可以实现，时间复杂度为O(nlogk)

代码：

function maxSlidingWindow(nums, k) {
  if (k <= 0 || nums.length === 0) {
    return [];
  }

  const result = [];
  const deque = []; // 双向队列

  for (let i = 0; i < nums.length; i++) {
    // 检查队首元素是否超出滑动窗口的范围
    if (deque.length > 0 && deque[0] <= i - k) {
      deque.shift();
    }

    // 与队列中的元素进行比较，保持队列中的元素有序
    while (deque.length > 0 && nums[deque[deque.length - 1]] <= nums[i]) {
      deque.pop();
    }

    deque.push(i); // 将当前元素的索引插入到队列的尾部

    // 检查当前索引是否已经达到滑动窗口的大小 k
    if (i >= k - 1) {
      result.push(nums[deque[0]]); // 队首元素即为当前窗口的最大值
    }
  }

  return result;
}

前 K 个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

输入: nums = [1], k = 1
输出: [1]

提示：

1 <= nums.length <= 105
k 的取值范围是 [1, 数组中不相同的元素的个数]
题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

**进阶：**你所设计算法的时间复杂度必须优于 O(n log n) ，其中 n 是数组大小。

解法一：统计

遍历数组，使用哈希 map 记录每个元素出现次数（元素作为key，出现次数作为值）；
遍历哈希map，将哈希 Map 中每个元素组成一个数组 [元素值，出现频率]，存入一个新的数组；
将新的数组根据第二个出现频率进行排序；
取数组中前 k 个元素即可；

function topKFrequent(nums: number[], k: number): number[] {
    let map: object = {}
    let res: number[] = []
    let temp: number[][] = []
    for (let i = 0; i < nums.length; i++) {
        let key = nums[i]
        if (map[key] !== undefined) {
            map[key]++
        } else {
            map[key] = 1
        }
    }

    Object.keys(map).forEach(key => {
        let item = [key, map[key]] //以 [当前值,出现频率] 保存
        temp.push(item)
    })
    temp = temp.sort((num1, num2) => num2[1] - num1[1])
    res = temp.slice(0, k).map(item => item[0])
    return res
};

解法二：哈希表 + 优先队列

使用哈希表记录下数组中各个元素的频数。
然后将哈希表中的元素去重，转换为新数组。时间复杂度 𝑂(𝑛)，空间复杂度 𝑂(𝑛)。
使用二叉堆构建优先队列，优先级为元素频数。此时堆顶元素即为频数最高的元素。时间复杂度 𝑂(𝑛)，空间复杂度 𝑂(𝑛)。
将堆顶元素加入到答案数组中，进行出队操作。时间复杂度𝑂(log⁡𝑛)。
- 出队操作：交换堆顶元素与末尾元素，将末尾元素已移出堆。继续调整大顶堆。
不断重复第 4 步，直到 𝑘 次结束。调整 𝑘 次的时间复杂度 𝑂(𝑛×log⁡𝑛)。

class Heapq {
    // 堆调整方法：调整为大顶堆
    heapAdjust(nums: number[], numsDict: { [key: number]: number }, index: number, end: number): void {
        let left = index * 2 + 1;
        let right = left + 1;
        while (left <= end) {
            // 当前节点为非叶子结点
            let max_index = index;
            if (numsDict[nums[left]] > numsDict[nums[max_index]]) {
                max_index = left;
            }
            if (right <= end && numsDict[nums[right]] > numsDict[nums[max_index]]) {
                max_index = right;
            }
            if (index === max_index) {
                // 如果不用交换，则说明已经交换结束
                break;
            }
            [nums[index], nums[max_index]] = [nums[max_index], nums[index]];
            // 继续调整子树
            index = max_index;
            left = index * 2 + 1;
            right = left + 1;
        }
    }

    // 将数组构建为二叉堆
    heapify(nums: number[], numsDict: { [key: number]: number }): void {
        const size = nums.length;
        // (size - 2) // 2 是最后一个非叶节点，叶节点不用调整
        for (let i = (size - 2) >> 1; i >= 0; i--) {
            // 调用调整堆函数
            this.heapAdjust(nums, numsDict, i, size - 1);
        }
    }

    // 入队操作
    heappush(nums: number[], numsDict: { [key: number]: number }, value: number): void {
        nums.push(value);
        const size = nums.length;
        let i = size - 1;
        // 寻找插入位置
        while ((i - 1) >> 1 >= 0) {
            const cur_root = (i - 1) >> 1;
            // value 小于当前根节点，则插入到当前位置
            if (numsDict[nums[cur_root]] > numsDict[value]) {
                break;
            }
            // 继续向上查找
            nums[i] = nums[cur_root];
            i = cur_root;
        }
        // 找到插入位置或者到达根位置，将其插入
        nums[i] = value;
    }

    // 出队操作
    heappop(nums: number[], numsDict: { [key: number]: number }): number {
        const size = nums.length;
        [nums[0], nums[-1]] = [nums[-1], nums[0]];
        // 得到最大值（堆顶元素）然后调整堆
        const top = nums.pop();
        if (size > 0) {
            this.heapAdjust(nums, numsDict, 0, size - 2);
        }
        return top;
    }
}

class Solution {
    topKFrequent(nums: number[], k: number): number[] {
        // 统计元素频数
        const numsDict: { [key: number]: number } = {};
        for (const num of nums) {
            if (numsDict[num]) {
                numsDict[num] += 1;
            } else {
                numsDict[num] = 1;
            }
        }

        // 使用 set 方法去重，得到新数组，减少重复操作
        const newNums = Array.from(new Set(nums));
        const size = newNums.length;

        const heap = new Heapq();
        const queue: number[] = [];
        // 遍历数组，将每个元素入优先队列
        for (const num of newNums) {
            heap.heappush(queue, numsDict, num);
        }

        const res: number[] = [];
        // 将优先队列出队列
        for (let i = 0; i < k; i++) {
            res.push(heap.heappop(queue, numsDict));
        }
        return res;
    }
}

// 使用示例
const solution = new Solution();
const res = solution.topKFrequent([1, 1, 2, 2, 3], 2);
console.log(res); // 输出: [1, 2]