栈
栈
定义和特点
- 栈是一种线性数据结构,具有后进先出(LIFO)的特性。
- 可以类比为一叠盘子,只能从顶部放入和取出元素。
- 可以使用数组的
push()和pop()方法来实现。
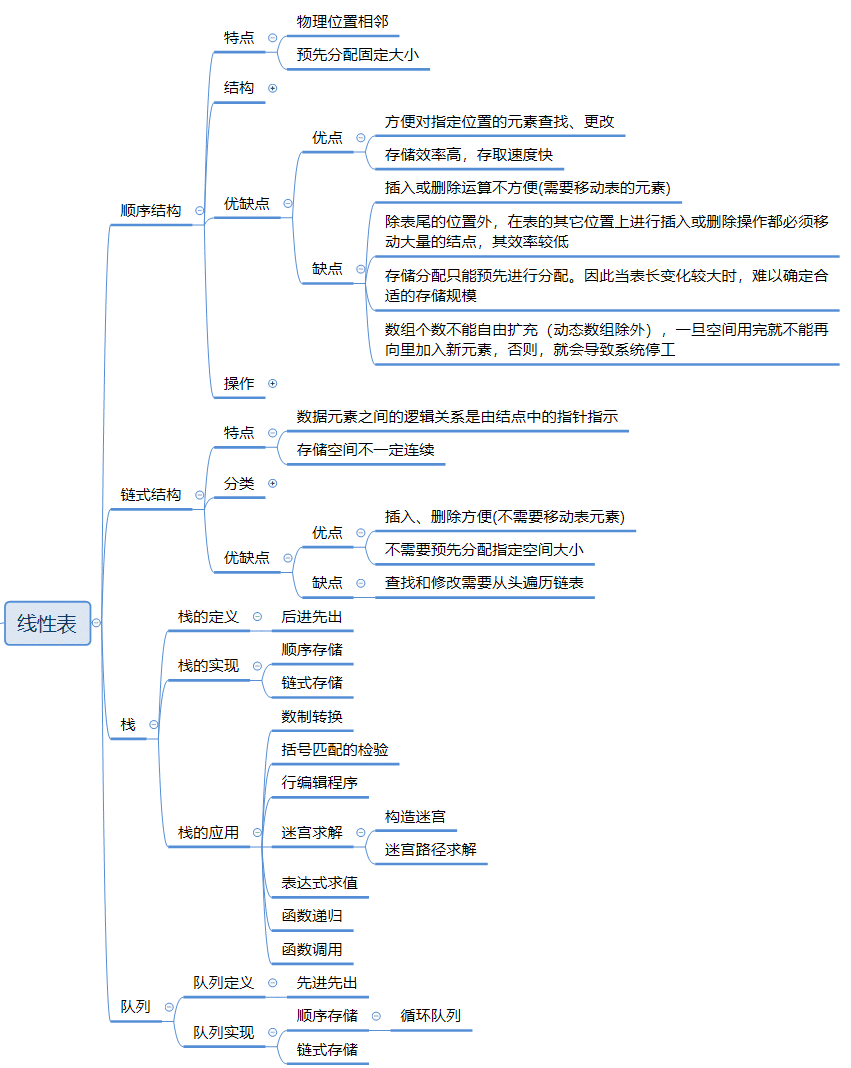
分类
「顺序栈」:即堆栈的顺序存储结构。利用一组地址连续的存储单元依次存放自栈底到栈顶的元素,同时使用指针 𝑡𝑜𝑝 指示栈顶元素在顺序栈中的位置。
「链式栈」:即堆栈的链式存储结构。利用单链表的方式来实现堆栈。栈中元素按照插入顺序依次插入到链表的第一个节点之前,并使用栈顶指针 𝑡𝑜𝑝 指示栈顶元素,𝑡𝑜𝑝 永远指向链表的头节点位置。
基本操作
顺序栈
- 入栈(Push):将元素放入栈顶。
- 出栈(Pop):从栈顶移除元素,并返回移除的元素。
- 获取栈顶元素(Top):返回栈顶的元素,并不移除该元素。
- 判断栈是否为空(isEmpty):检查栈是否为空。
class Stack {
constructor(size = 100) {
this.stack = [];
this.maxSize = size; // 注意这里我们使用maxSize而不是size,因为我们实际上不限制数组的大小
this.top = -1;
}
// 判断栈是否为空
isEmpty() {
return this.top === -1;
}
// 判断栈是否已满(但在这个实现中,我们实际上不限制栈的大小)
// 如果需要限制,可以在push方法中添加逻辑
isFull() {
return this.stack.length === this.maxSize;
}
// 入栈操作
push(value) {
if (this.isFull()) {
throw new Error('Stack is full');
} else {
this.stack.push(value);
this.top = this.stack.length - 1; // 直接使用stack.length - 1来获取顶部索引
}
}
// 出栈操作
pop() {
if (this.isEmpty()) {
throw new Error('Stack is empty');
} else {
this.stack.pop();
this.top = this.stack.length - 1; // 更新顶部索引
}
}
// 获取栈顶元素
peek() {
if (this.isEmpty()) {
throw new Error('Stack is empty');
} else {
return this.stack[this.stack.length - 1]; // 直接使用stack.length - 1来获取顶部元素
}
}
}
// 使用示例
let stack = new Stack();
stack.push(1);
stack.push(2);
console.log(stack.peek()); // 输出 2
stack.pop();
console.log(stack.peek()); // 输出 1
链式栈
class Node {
constructor(value) {
this.value = value;
this.next = null;
}
}
class Stack {
constructor() {
this.top = null;
}
// 判断栈是否为空
isEmpty() {
return this.top === null;
}
// 入栈操作
push(value) {
const cur = new Node(value);
cur.next = this.top;
this.top = cur;
}
// 出栈操作
pop() {
if (this.isEmpty()) {
throw new Error('Stack is empty');
} else {
const cur = this.top;
this.top = this.top.next;
// 在JavaScript中,不需要显式地删除对象(通过del关键字),因为垃圾回收器会处理它
}
}
// 获取栈顶元素
peek() {
if (this.isEmpty()) {
throw new Error('Stack is empty');
} else {
return this.top.value;
}
}
}
// 使用示例
let stack = new Stack();
stack.push(1);
stack.push(2);
console.log(stack.peek()); // 输出 2
stack.pop();
console.log(stack.peek()); // 输出 1
应用场景
- 逆序输出、括号匹配、函数调用和递归等。
单调栈
单调栈(Monotone Stack):一种特殊的栈。在栈的「先进后出」规则基础上,要求「从 栈顶 到 栈底 的元素是单调递增(或者单调递减)」。其中满足从栈顶到栈底的元素是单调递增的栈,叫做「单调递增栈」。满足从栈顶到栈底的元素是单调递减的栈,叫做「单调递减栈」。
注意:这里定义的顺序是从「栈顶」到「栈底」。有的文章里是反过来的。本文全文以「栈顶」到「栈底」的顺序为基准来描述单调栈。
单调递增栈
单调递增栈:只有比栈顶元素小的元素才能直接进栈,否则需要先将栈中比当前元素小的元素出栈,再将当前元素入栈。
这样就保证了:栈中保留的都是比当前入栈元素大的值,并且从栈顶到栈底的元素值是单调递增的。
单调递增栈的入栈、出栈过程如下:
- 假设当前进栈元素为 𝑥,如果 𝑥 比栈顶元素小,则直接入栈。
- 否则从栈顶开始遍历栈中元素,把小于 𝑥 或者等于 𝑥 的元素弹出栈,直到遇到一个大于 𝑥 的元素为止,然后再把 𝑥 压入栈中。
function monotoneIncreasingStack(nums) {
let stack = [];
for (let num of nums) {
while (stack.length > 0 && num >= stack[stack.length - 1]) {
stack.pop(); // 弹出的元素不属于单调递增栈
}
stack.push(num);
}
return stack; // 如果需要返回最终的栈内容,可以添加这一行
}
// 使用示例
let nums = [1, 3, 2, 4, 5, 4, 6];
let result = monotoneIncreasingStack(nums);
console.log(result); // 打印结果(如果return语句包含在函数中)
// 或者,如果你只想在控制台中看到栈的变化,可以在循环内部打印stack
下面我们以数组 [2,7,5,4,6,3,4,2] 为例,模拟一下「单调递增栈」的进栈、出栈过程。具体过程如下:
- 数组元素: [2, 7, 5, 4, 6, 3, 4, 2] ,遍历顺序为从左到右。
| 第 i 步 | 待插入元素 | 操 作 | 结 果(左侧为栈底) | 作 用 |
|---|---|---|---|---|
| 1 | 2 | 2 入栈 | [2] | 元素 2 的左侧无比 2 大的元素 |
| 2 | 7 | 2 出栈,7 入栈 | [7] | 元素 7 的左侧无比 7 大的元素 |
| 3 | 5 | 5 入栈 | [7, 5] | 元素 5 的左侧第一个比 5 大的元素为:7 |
| 4 | 4 | 4 入栈 | [7, 5, 4] | 元素 4 的左侧第一个比 4 大的元素为:5 |
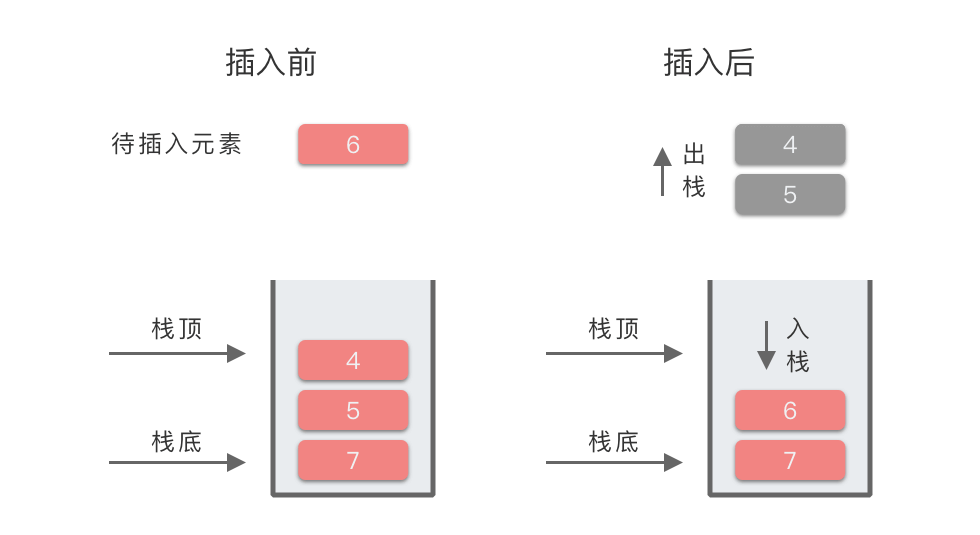
| 5 | 6 | 4 出栈,5 出栈,6 入栈 | [7, 6] | 元素 6 的左侧第一个比 6 大的元素为:7 |
| 6 | 3 | 3 入栈 | [7, 6, 3] | 元素 3 的左侧第一个比 3 大的元素为:6 |
| 7 | 4 | 3 出栈,4 入栈 | [7, 6, 4] | 元素 4 的左侧第一个比 4 大的元素为:6 |
| 8 | 2 | 2 入栈 | [7, 6, 4, 2] | 元素 2 的左侧第一个比 2 大的元素为:4 |
最终栈中元素为 [7,6,4,2]。因为从栈顶(右端)到栈底(左侧)元素的顺序为 2,4,6,7,满足递增关系,所以这是一个单调递增栈。
我们以上述过程第 5 步为例,所对应的图示过程为:
单调递减栈
单调递减栈:只有比栈顶元素大的元素才能直接进栈,否则需要先将栈中比当前元素大的元素出栈,再将当前元素入栈。
这样就保证了:栈中保留的都是比当前入栈元素小的值,并且从栈顶到栈底的元素值是单调递减的。
单调递减栈的入栈、出栈过程如下:
- 假设当前进栈元素为 𝑥,如果 𝑥 比栈顶元素大,则直接入栈。
- 否则从栈顶开始遍历栈中元素,把大于 𝑥 或者等于 𝑥 的元素弹出栈,直到遇到一个小于 𝑥 的元素为止,然后再把 𝑥 压入栈中。
function monotoneDecreasingStack(nums) {
let stack = [];
for (let num of nums) {
while (stack.length > 0 && num <= stack[stack.length - 1]) {
stack.pop();
}
stack.push(num);
}
return stack; // 如果需要返回最终的栈内容,可以添加这一行
}
// 使用示例
let nums = [1, 3, 2, 4, 5, 4, 6];
let result = monotoneDecreasingStack(nums);
console.log(result); // 打印结果(如果return语句包含在函数中)
下面我们以数组 [4,3,2,5,7,4,6,8] 为例,模拟一下「单调递减栈」的进栈、出栈过程。具体过程如下:
- 数组元素: [4, 3, 2, 5, 7, 4, 6, 8] ,遍历顺序为从左到右。
| 第 i 步 | 待插入元素 | 操 作 | 结 果(左侧为栈底) | 作用 |
|---|---|---|---|---|
| 1 | 4 | 4 入栈 | [4] | 元素 4 的左侧无比 4 小的元素 |
| 2 | 3 | 4 出栈,3 入栈 | [3] | 元素 3 的左侧无比 3 小的元素 |
| 3 | 2 | 3 出栈,2 入栈 | [2] | 元素 2 的左侧无比 2 小的元素 |
| 4 | 5 | 5 入栈 | [2, 5] | 元素 5 的左侧第一个比 5 小的元素是:2 |
| 5 | 7 | 7 入栈 | [2, 5, 7] | 元素 7 的左侧第一个比 7 小的元素是:5 |
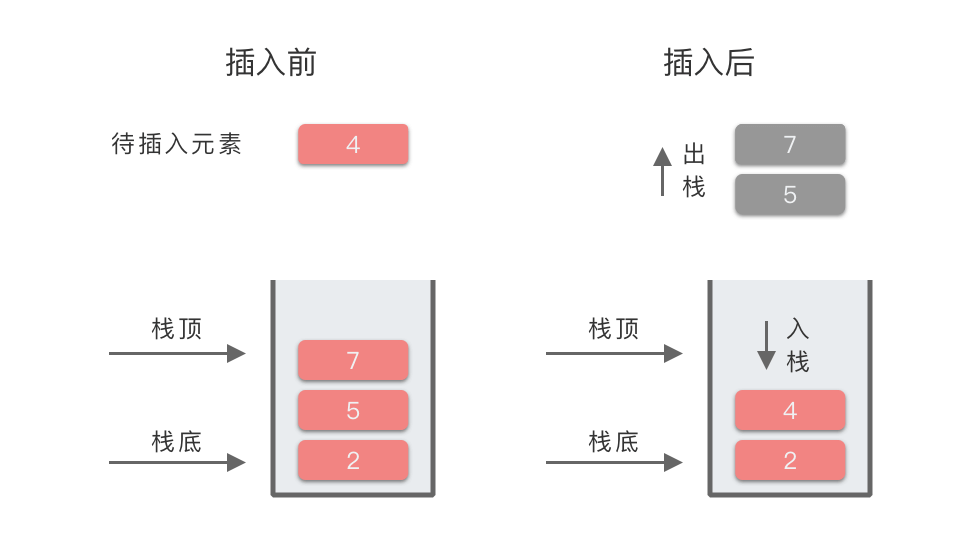
| 6 | 4 | 7 出栈,5 出栈,4 入栈 | [2, 4] | 元素 4 的左侧第一个比 4 小的元素是:2 |
| 7 | 6 | 6 入栈 | [2, 4, 6] | 元素 6 的左侧第一个比 6 小的元素是:4 |
| 8 | 8 | 8 入栈 | [2, 4, 6, 8] | 元素 8 的左侧第一个比 8 小的元素是:6 |
最终栈中元素为 [2,4,6,8]。因为从栈顶(右端)到栈底(左侧)元素的顺序为 8,6,4,2,满足递减关系,所以这是一个单调递减栈。
我们以上述过程第 6 步为例,所对应的图示过程为:
单调栈适用场景
单调栈可以在时间复杂度为 𝑂(𝑛) 的情况下,求解出某个元素左边或者右边第一个比它大或者小的元素。
所以单调栈一般用于解决一下几种问题:
寻找左侧第一个比当前元素大的元素:
- 从左到右遍历元素,构造单调递增栈(从栈顶到栈底递增):
- 一个元素左侧第一个比它大的元素就是将其「插入单调递增栈」时的栈顶元素。
- 如果插入时的栈为空,则说明左侧不存在比当前元素大的元素。
寻找左侧第一个比当前元素小的元素:
- 从左到右遍历元素,构造单调递减栈(从栈顶到栈底递减):
- 一个元素左侧第一个比它小的元素就是将其「插入单调递减栈」时的栈顶元素。
- 如果插入时的栈为空,则说明左侧不存在比当前元素小的元素。
寻找右侧第一个比当前元素大的元素:
从左到右遍历元素,构造单调递增栈(从栈顶到栈底递增):
- 一个元素右侧第一个比它大的元素就是将其「弹出单调递增栈」时即将插入的元素。
- 如果该元素没有被弹出栈,则说明右侧不存在比当前元素大的元素。
寻找右侧第一个比当前元素小的元素:
从左到右遍历元素,构造单调递减栈(从栈顶到栈底递减):
一个元素右侧第一个比它小的元素就是将其「弹出单调递减栈」时即将插入的元素。
如果该元素没有被弹出栈,则说明右侧不存在比当前元素小的元素。
总结:
- 查找 「比当前元素大的元素」 就用 单调递增栈,查找 「比当前元素小的元素」 就用 单调递减栈。
- 从 「左侧」 查找就看 「插入栈」 时的栈顶元素,从 「右侧」 查找就看 「弹出栈」 时即将插入的元素。
算法题
顺序栈题集
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 1047 | 删除字符串中的所有相邻重复项 | 栈、字符串 | 简单 |
| 0155 | 最小栈 | 栈、设计 | 中等 |
| 0020 | 有效的括号 | 栈、字符串 | 简单 |
| 0227 | 基本计算器 II | 栈、数学、字符串 | 中等 |
| 0739 | 每日温度 | 栈、数组、单调栈 | 中等 |
| 0150 | 逆波兰表达式求值 | 栈、数组、数学 | 中等 |
| 0232 | 用栈实现队列 | 栈、设计、队列 | 简单 |
| 剑指 Offer 09 | 用两个栈实现队列 | 栈、设计、队列 | 简单 |
| 0394 | 字符串解码 | 栈、递归、字符串 | 中等 |
| 0032 | 最长有效括号 | 栈、字符串、动态规划 | 困难 |
| 0946 | 验证栈序列 | 栈、数组、模拟 | 中等 |
| 剑指 Offer 06 | 从尾到头打印链表 | 栈、递归、链表、双指针 | 简单 |
| 0071 | 简化路径 | 栈、字符串 | 中等 |
用两个队列实现一个栈(简单)
题目:用两个队列实现一个栈
思路
- 创建两个队列,分别命名为
queue1和queue2。- 入栈操作:
- 将元素添加到非空的队列中(初始时选择其中一个队列)。
- 如果两个队列都为空,可以选择任意一个队列添加元素。
- 出栈操作:
- 将非空队列中的元素逐个出队并入队到另一个空队列,直到队列中只剩下一个元素。
- 移除最后剩下的元素并返回,即为出栈的元素。
- 获取栈顶元素操作:
- 同出栈操作,将非空队列中的元素逐个出队并入队到另一个空队列,直到队列中只剩下一个元素。
- 返回最后剩下的元素,即为栈顶元素。
代码:
class Stack {
constructor() {
this.queue1 = [];
this.queue2 = [];
}
push(element) {
if (this.queue1.length === 0) {
this.queue2.push(element);
} else {
this.queue1.push(element);
}
}
pop() {
if (this.queue1.length === 0 && this.queue2.length === 0) {
return null;
}
let nonEmptyQueue, emptyQueue;
if (this.queue1.length === 0) {
nonEmptyQueue = this.queue2;
emptyQueue = this.queue1;
} else {
nonEmptyQueue = this.queue1;
emptyQueue = this.queue2;
}
while (nonEmptyQueue.length > 1) {
emptyQueue.push(nonEmptyQueue.shift());
}
return nonEmptyQueue.shift();
}
top() {
if (this.queue1.length === 0 && this.queue2.length === 0) {
return null;
}
let nonEmptyQueue, emptyQueue;
if (this.queue1.length === 0) {
nonEmptyQueue = this.queue2;
emptyQueue = this.queue1;
} else {
nonEmptyQueue = this.queue1;
emptyQueue = this.queue2;
}
while (nonEmptyQueue.length > 1) {
emptyQueue.push(nonEmptyQueue.shift());
}
const topElement = nonEmptyQueue.shift();
emptyQueue.push(topElement);
return topElement;
}
isEmpty() {
return this.queue1.length === 0 && this.queue2.length === 0;
}
}
// 示例用法
const stack = new Stack();
stack.push(1);
stack.push(2);
stack.push(3);
console.log(stack.top()); // 输出 3
console.log(stack.pop()); // 输出 3
console.log(stack.isEmpty()); // 输出 false
两个栈来实现一个队列(简单)
题目:两个栈来实现一个队列
思路:
- 创建两个栈,分别命名为
stack1和stack2。- 入队操作:
- 将元素压入
stack1栈中。- 出队操作:
- 如果
stack2不为空,直接从stack2栈顶弹出元素并返回。- 如果
stack2为空,将stack1中的元素逐个弹出并压入stack2,然后从stack2栈顶弹出元素并返回。- 获取队头元素操作:
- 如果
stack2不为空,返回stack2栈顶元素。- 如果
stack2为空,将stack1中的元素逐个弹出并压入stack2,然后返回stack2栈顶元素。
代码:
class Queue {
constructor() {
this.stack1 = [];
this.stack2 = [];
}
enqueue(element) {
this.stack1.push(element);
}
dequeue() {
if (this.stack2.length === 0) {
while (this.stack1.length > 0) {
this.stack2.push(this.stack1.pop());
}
}
return this.stack2.pop() || null;
}
front() {
if (this.stack2.length === 0) {
while (this.stack1.length > 0) {
this.stack2.push(this.stack1.pop());
}
}
return this.stack2[this.stack2.length - 1] || null;
}
isEmpty() {
return this.stack1.length === 0 && this.stack2.length === 0;
}
}
// 示例用法
const queue = new Queue();
queue.enqueue(1);
queue.enqueue(2);
queue.enqueue(3);
console.log(queue.front()); // 输出 1
console.log(queue.dequeue()); // 输出 1
console.log(queue.isEmpty()); // 输出 false
包含min函数的栈(简单)
题目:
定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
思路:
题意理解:min 函数能够获取栈中最小元素,在栈进行入栈和出栈操作后,都能获取当前栈最小元素;
创建两个栈,一个称为
dataStack存储数据元素,另一个称为minStack存储最小元素。入栈操作:
- 将元素压入
dataStack栈中。- 如果
minStack为空,或者新入栈的元素小于等于minStack栈顶元素,则将新元素也压入minStack栈中。出栈操作:
- 从
dataStack栈顶弹出元素,并将其返回。- 如果弹出的元素等于
minStack栈顶元素,则也从minStack栈顶弹出元素。获取栈中最小元素操作:
- 直接返回
minStack栈顶元素,即为栈中的最小元素。以数据[3,4,2,7,9,0]为例,让这组数字依次如栈,则栈和其对应的最小值栈如下:
代码
class MinStack {
constructor() {
this.dataStack = []; // 存储数据元素的栈
this.minStack = []; // 存储最小元素的栈
}
push(element) {
this.dataStack.push(element);
if(minStack.length === 0 || element < this.min()){
minStack.push(element);
}else{
minStack.push(this.min());
}
}
pop() {
const poppedElement = this.dataStack.pop();
if (poppedElement === this.minStack[this.minStack.length - 1]) {
this.minStack.pop();
}
return poppedElement;
}
min() {
return this.minStack[this.minStack.length - 1];
}
}
// 示例用法
const stack = new MinStack();
stack.push(3);
stack.push(2);
stack.push(5);
console.log(stack.min()); // 输出 2
stack.pop();
console.log(stack.min()); // 输出 2
stack.push(1);
console.log(stack.min()); // 输出 1
栈的压入、弹出序列(简单)
题目:
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列
1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
思路:
题意理解:
- 栈的弹出顺序并是指在栈的压入过程中,任意一次压入时再弹出,记录的弹出的顺序;
- 题中只要求判断第二个栈是否为第一个栈的可能弹出顺序,并未要求列出弹出顺序,第一个栈的弹出顺序有很多种;
解题思路:
- 使用辅助栈和模拟的方法来解决:
- 初始化一个辅助栈和一个指针
pushIndex,pushIndex指向辅助栈,初始时pushIndex的值为 0,既辅助栈为空。- 遍历弹出序列,依次取出每一个元素:
- 如果辅助栈的栈顶元素(起始辅助栈为空)不等于当前弹出序列的元素,表示还需要继续压栈,将压栈序列中
pushIndex之前的元素依次压入辅助栈,直到找到与当前弹出序列元素相等的元素为止。- 如果辅助栈的栈顶元素等于当前弹出序列的元素,表示可以直接弹出,将栈顶元素弹出,然后继续遍历下一个弹出序列元素。
- 如果弹出序列遍历完成后,辅助栈为空,表示该弹出序列是可能的,否则不可能。
举例:
- 例如序列
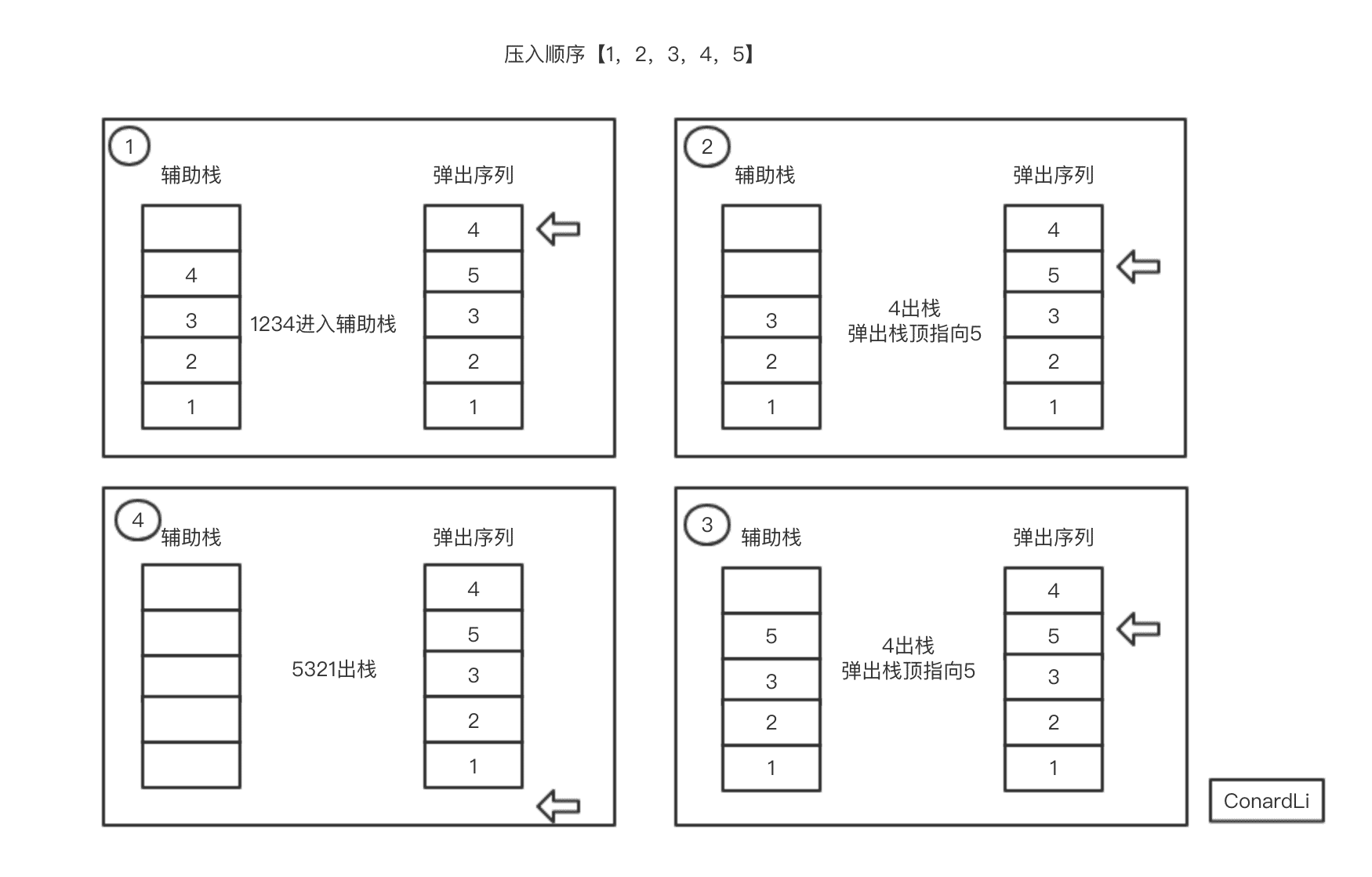
1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,判断过程如下:
- 起始辅助栈为空,弹出序列第一个元素为 4,序列
1,2,3,入栈,每次栈顶元素不等于 4,继续入栈直到 4 入辅助栈顶,此时辅助栈为:1,2,3,4;- 栈顶 4 等于辅助栈栈顶 4,辅助栈 4 出栈,记录出栈数字 4,弹出序列下移动一个;
- 此时弹出栈栈顶为 3,弹出序列为 5,不相等,辅助栈继续将剩余元素 5 入栈;
- 此时辅助栈栈顶元素 5 等于 弹出序列当前指针指向元素 5, 辅助栈出栈 5,弹出序列下移动一个;
- 此时辅助栈剩余元素与弹出序列剩余元素顺序相同,辅助栈出栈,弹出序列下移动;直到辅助栈为空并且没有需要入栈的元素,则序列
4,5,3,2,1是该压栈序列对应的一个弹出序列。
代码:
function isPopOrder(pushSequence, popSequence) {
if (pushSequence.length !== popSequence.length) {
return false;
}
const stack = [];
let pushIndex = 0;//指向栈序列
for (let i = 0; i < popSequence.length; i++) {//遍历弹出序列
const current = popSequence[i];//获取弹出序列第一个元素
// 栈为空或栈顶元素不等于弹出序列
while (stack.length === 0 || stack[stack.length - 1] !== current) {
if (pushIndex >= pushSequence.length) { //栈指针超出序列,退出
return false;
}
stack.push(pushSequence[pushIndex]); // 入栈序列元素入栈
pushIndex++;
}
// 栈顶元素等于弹出序列顶部元素,栈顶出栈
if (stack[stack.length - 1] === current) {
stack.pop();
}
}
return stack.length === 0;
}
// 示例用法
console.log(isPopOrder([1, 2, 3, 4, 5], [4, 5, 3, 2, 1])); // 输出 true
console.log(isPopOrder([1, 2, 3, 4, 5], [4, 3, 5, 1, 2])); // 输出 false
有效括号序列(简单)
题目:
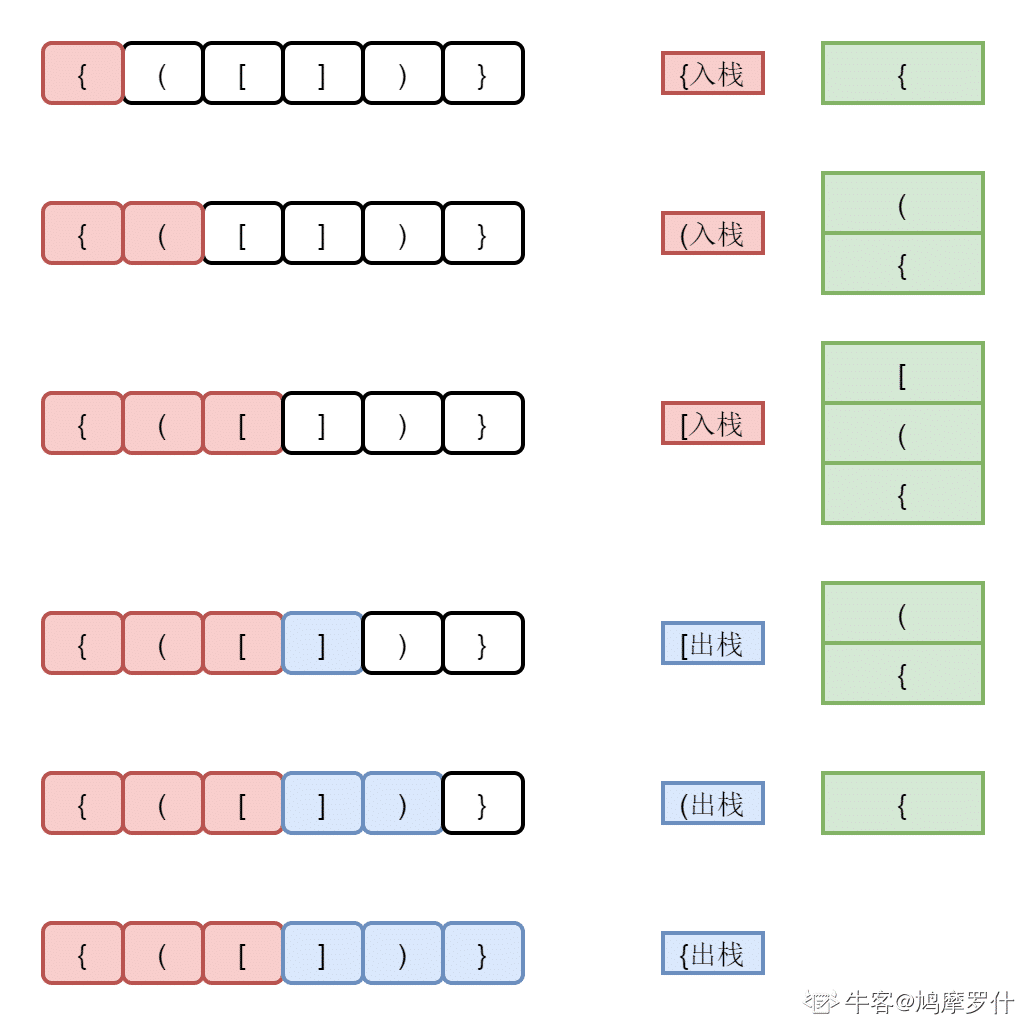
给出一个仅包含字符'(',')','{','}','['和']',的字符串,判断给出的字符串是否是合法的括号序列 括号必须以正确的顺序关闭,"()"和"()[]{}"都是合法的括号序列,但"(]"和"([)]"不合法。
数据范围:字符串长度 0≤n≤10000
要求:空间复杂度O*(n),时间复杂度 O*(n)
思路一:
解题思路:
- 创建一个空栈。
- 遍历输入的字符串,对于每个字符:
- 如果是左括号('(', '{', '['),将其推入栈中。
- 如果是右括号(')', '}', ']'),检查栈是否为空:
- 如果栈为空,说明右括号多于左括号,返回 false。
- 如果栈不为空,将栈顶元素出栈,并与当前右括号进行匹配:
- 如果匹配成功,继续遍历下一个字符。
- 如果匹配失败,返回 false。
- 遍历完字符串后,检查栈是否为空:
- 如果栈为空,说明所有括号都匹配成功,返回 true。
- 如果栈不为空,说明左括号多于右括号,返回 false。
代码一:
function isValidParentheses(s) {
if(s.length<0 || s.length > 10000) return false;
const stack = []; // 创建空栈
for (let i = 0; i < s.length; i++) {
const char = s[i];
if (char === '(' || char === '{' || char === '[') {
stack.push(char); // 左括号入栈
} else {
if (stack.length === 0) {
return false; // 右括号多于左括号,返回 false
}
const top = stack.pop(); // 弹出栈顶元素
if (
(char === ')' && top !== '(') ||
(char === '}' && top !== '{') ||
(char === ']' && top !== '[')
) {
return false; // 括号不匹配,返回 false
}
}
}
return stack.length === 0; // 栈为空则括号匹配成功,返回 true,否则返回 false
}
module.exports = {
isValid: isValidParentheses,
};
代码二:使用栈和 map 代替 if 判断
/**
*
* @param s string字符串
* @return bool布尔型
*/
function isValid( s ) {
let stack = [];
let pair = {
'{': '}',
'(': ')',
'[': ']'
};
for (let i = 0; i < s.length; i++) {
if (pair[s[i]]) stack.push(s[i]); // 左括号入栈
else if (pair[stack[stack.length - 1]] !== s[i]) return false; // 匹配到右括号,栈顶元素是否与当前括号不匹配,返回false
else stack.pop();// 匹配到右括号,栈顶元素是否与当前括号匹配,栈顶出栈
}
return stack.length <= 0;
}
module.exports = {
isValid : isValid
};
思路二:
- 分析:题目中仅包含字符串,如果是合法字符串,那么括号内部一定有一个正确的左右括号,因此可以使用正则匹配,将最中心的左右括号去除,剩余的括号依然可以组成合法的左右括号的话,那么就可以继续正则去除;
- 注意:
- 该代码的思路是通过不断替换括号对来判断合法性,但并没有使用栈这种数据结构。
- 相比使用栈的方法,该方法的时间复杂度较高,因为每次替换都需要遍历整个字符串。
- 同时,该方法也无法处理括号嵌套的情况,例如 "(())" 是合法的括号序列,但该方法无法正确判断。
- 因此,建议使用栈的方法来解决该题目。
代码:
function isValid(s) {
// write code here
let len = s.length
for (let i = 0; i < len / 2; i++){
s = s.replace("{}", "").replace("()", "").replace("[]", "");
console.log(s)
}
return s === ''
}
module.exports = {
isValid: isValid,
};
数制转换(简单)
题目:
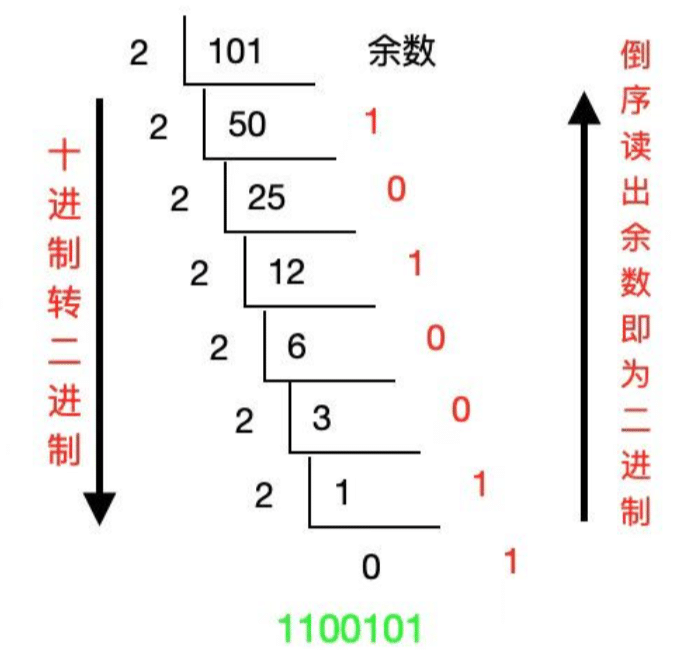
编写一个函数,实现十进制数转换任意进制数
解法一:使用队列:
定义一个队列,用于存储转换后的数字的每一位。
定义一个变量
num,用于保存待转换的十进制数。定义一个变量
base,表示目标进制数。进入循环,直到 num 等于 0:
- 求余数:将
num对base取余,得到当前位的数字。- 将余数入队:将余数入队,表示当前位的数字。
- 更新
num:将num除以base,向下取整,更新num的值。循环结束后,队列中的每个元素就是转换后的数字的每一位。
弹出队列元素:从队列中依次弹出元素,组成转换后的数值。
返回转换后的数值。
代码:
class Queue {
constructor() {
this.items = [];
}
enqueue(item) {
this.items.push(item);
}
dequeue() {
return this.items.shift();
}
isEmpty() {
return this.items.length === 0;
}
}
/**
* params {} decimal 十进制数
* params {} base 转换进制
**/
function decimalToBase(decimal, base) {
const queue = new Queue();
let num = decimal;
if (num === 0) { // 商结果为0,出队列
queue.enqueue(num);
}
while (num !== 0) {
const remainder = num % base; // 取模获得余数
queue.enqueue(remainder); // 余数入队列
num = Math.floor(num / base); // 除法获得商
}
let result = "";
while (!queue.isEmpty()) {
result += queue.dequeue();
}
return result;
}
// 示例用法
const decimalNumber = 123; // 十进制数
const base = 2; // 目标进制数
const convertedNumber = decimalToBase(decimalNumber, base);
console.log(convertedNumber); // 输出: "1111011"
解法二:使用数组
- 定义一个空字符串或数组,用于存储转换后的结果。
- 使用循环,将输入的十进制数不断除以目标进制数,直到商为 0。
- 在每一次循环中,将当前的余数添加到结果中,并将商更新为上一步的商。
- 当商为 0 时,循环结束。
- 将结果反转,得到最终转换后的任意进制数。
代码:
/**
* params {} decimal 十进制数
* params {} base 转换进制
**/
function decimalToArbitraryBase(decimal, base) {
if (decimal === 0) {
return "0"; // 十进制数为 0,则结果为 "0"
}
const digits = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"; // 可用的数字字符
let result = "";
let quotient = Math.abs(decimal); // 取绝对值,以处理负数的情况
while (quotient > 0) {
const remainder = quotient % base; // 取模获取当前的余数
result = digits[remainder] + result; // 根据余数获取数字,并拼接结果
quotient = Math.floor(quotient / base); // 获取商:更新商为上一步的商
}
return decimal < 0 ? "-" + result : result; // 处理负数的情况
}
// 示例用法
const decimal = 123; // 十进制数
const base = 16; // 目标进制数
const result = decimalToArbitraryBase(decimal, base);
console.log(result); // 输出: "7B"
表达式求值(中等)
题目:
请写一个整数计算器,支持加减乘三种运算和括号。
数据范围:0≤∣s∣≤100,保证计算结果始终在整型范围内
要求:空间复杂度:O*(*n),时间复杂度O(n)
思路:
对于上述两个要求,我们要考虑的是两点,一是处理运算优先级的问题,二是处理括号的问题。
处理优先级问题:那必定是乘号有着优先运算的权利,加号减号先一边看
- 我们甚至可以把减号看成加一个数的相反数,则这里只有乘法和加法,那我们优先处理乘法;
- 遇到乘法,把前一个数和后一个数乘起来;
- 遇到加法就把这些数字都暂时存起来;
- 最后乘法处理完了,就剩余加法,把之前存起来的数字都相加就好了。
处理括号的问题:
- 我们可以将括号中的部分看成一个新的表达式,即一个子问题,因此可以将新的表达式递归地求解,得到一个数字,再运算;
- 终止条件: 每次遇到左括号意味着进入括号子问题进行计算,那么遇到右括号代表这个递归结束。
- 返回值: 将括号内部的计算结果值返回。
- 本级任务: 遍历括号里面的字符,进行计算。
具体做法:
- 使用栈辅助处理优先级,默认符号为加号。
- 遍历字符串,遇到数字,则将连续的数字字符部分转化为 number 数字。
- 遇到左括号,则将括号后的部分送入递归,处理子问题;遇到右括号代表已经到了这个子问题的结尾,结束继续遍历字符串,将子问题的加法部分相加为一个数字,返回。
- 当遇到符号的时候如果是+,得到的数字正常入栈,如果是-,则将其相反数入栈,如果是*,则将栈中内容弹出与后一个元素相乘再入栈。
- 最后将栈中剩余的所有元素,进行一次全部相加。
代码:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* 返回表达式的值
* @param s string字符串 待计算的表达式
* @return int整型
*/
function solve( s ) {//递归会出现深浅拷贝的问题,每次重新调用所有同名变量将改变
// write code here
let stack=[]; //辅助栈,记录数字和乘法计算结果
let sign='+'; // 符号记录
let i=0; // 遍历下标
let num=0; // 记录遍历到的数字
while(i<s.length){ // 遍历字符串
if(s[i]=='('){ // 遇到左括号,遍历查找该左括号对应的右括号
let flag=1; // flag 用于查找当前左括号对应的右括号
let star=i+1; //记录左括号内部字符串的开始下标
while(flag>0){ // 查找当前左括号对应的右括号, 当 flag == 0 表示找到
i++;
if(s[i]=='('){flag++;}
if(s[i]==')'){flag--;}
}
let end=i; // end 表示左括号对应的右括号下标,括号内为一个子表达式
let arr=s.slice(star,i); // 截取子表达式子串
num=solve(arr); // 递归计算子表达式
i=end; // 子表达式后一个下表开始重新遍历
}
else if(s[i]>='0'&&s[i]<='9'){ // 遍历字符串,遇到数字,则将连续的数字字符部分转化为int型数字。
num=num*10+Number(s[i])
}
if(s[i]<'0'||s[i]>'9'||i==s.length-1){ // 遇到非数字,则计算后入栈
if(sign=='+'){stack.push(num);} // 遇到加号直接入栈
if(sign=='-'){stack.push(num*(-1));} // 减法,则将数字转化为负数入栈
if(sign=='*'){stack.push(stack.pop()*num);} // 乘法,将栈顶元素和当前数字相乘后入栈
sign=s[i]; // 记录当前计算符号
num=0; // 重置数字记录
}
i++; // 指针后移
}
// 将栈内剩余元素全部累加
return stack.reduce(function(a,b){
return a+b;
})
}
module.exports = {
solve : solve
};
迷宫求解(教难)
题目:
给定一个
M * N的迷宫图,求一条从指定入口到出口的迷宫路径。
- 假设一个迷宫图如图所示(这里M=8,N=8),其中的每个方块用空白表示通道,用蓝色阴影表示障碍物。
- 一般情况下,所求迷宫路径是简单路径,即在求得的迷宫路径上不会重复出现同一方块。
- 一个迷官图的迷宫路径可能有多条,这些迷宫路径有长有短,
- 这里仅仅考虑用栈求一条从指定入口到出口的迷宫路径。
思路:
定义一个栈,用于存储当前的路径。
定义一个二维数组或矩阵来表示迷宫图,其中空白方块表示通道,蓝色阴影方块表示障碍物。
定义一个二维数组或矩阵来标记已经访问过的方块,初始化为全部为 false。
定义一个对象或元组来表示入口坐标,将入口坐标压入栈中。
进入循环,直到栈为空或找到出口坐标:
- 弹出栈顶元素,表示当前所在位置。
- 如果当前位置是出口坐标,表示找到了一条路径,循环结束。
- 否则,标记当前位置为已访问,并根据当前位置的四个相邻方块(上、下、左、右)进行判断:
- 如果相邻方块是通道且未访问过,将其坐标压入栈中。
如果栈为空,表示没有找到从入口到出口的路径;否则,栈中的元素就是路径的顺序,可以按照栈中元素的顺序输出路径。
代码:
class Stack {
constructor() {
this.items = [];
}
push(item) {
this.items.push(item);
}
pop() {
return this.items.pop();
}
isEmpty() {
return this.items.length === 0;
}
}
//`maze` 代表迷宫图的二维数组,`start` 代表入口坐标的数组 `[row, col]`,`end` 代表出口坐标的数组 `[row, col]`。
function findMazePath(maze, start, end) {
const stack = new Stack(); //用于存储当前的路径
const visited = [];//`visited`,用于标记已经访问过的方块
const directions = [[-1, 0], [1, 0], [0, -1], [0, 1]]; // 上下左右四个方向,用于在迷宫中移动
// 初始化 visited 数组,全部置为 false
for (let i = 0; i < maze.length; i++) {
visited[i] = [];
for (let j = 0; j < maze[i].length; j++) {
visited[i][j] = false;
}
}
stack.push(start);// 入口坐标入栈
// 循环查找栈内位置四个方便,直到栈内元素为空
while (!stack.isEmpty()) {
const current = stack.pop();//弹出栈顶元素,表示当前所在位置
if (current[0] === end[0] && current[1] === end[1]) {
// 找到出口坐标,返回路径
return stack.items;
}
// 标记当前位置已经访问过
visited[current[0]][current[1]] = true;
// 按照上下左右依次访问四个方向位置
for (const direction of directions) {
const newRow = current[0] + direction[0];
const newCol = current[1] + direction[1];
//相邻方块是通道且未访问过,将其坐标压入栈中
if (isValidMove(maze, newRow, newCol) && !visited[newRow][newCol]) {
stack.push([newRow, newCol]);
}
}
}
// 栈为空,表示没有找到路径
return null;
}
function isValidMove(maze, row, col) {
const numRows = maze.length;
const numCols = maze[0].length;
return row >= 0 && row < numRows && col >= 0 && col < numCols && maze[row][col] === " ";
}
// 示例用法
const maze = [
[" ", " ", " ", " ", " ", " ", " ", " "],
[" ", "X", "X", " ", " ", "X", "X", " "],
[" ", " ", " ", "X", " ", " ", " ", " "],
[" ", "X", " ", "X", " ", "X", " ", "X"],
[" ", " ", " ", " ", " ", " ", " ", " "],
[" ", "X", "X", "X", " ", "X", "X", " "],
[" ", " ", " ", " ", " ", " ", " ", " "],
[" ", " ", "X", "X", " ", "X", "X", " "]
];
const start = [0, 0]; // 入口坐标
const end = [7, 7]; // 出口坐标
/**
路径的函数是 `findMazePath`,它接受三个参数:`maze` 代表迷宫图的二维数组,`start` 代表入口坐标的数组 `[row, col]`,`end` 代表出口坐标的数组 `[row, col]`。
首先,我们定义一个栈 `stack`,用于存储当前的路径。我们还定义了一个二维数组 `visited`,用于标记已经访问过的方块。`directions` 是一个表示四个方向的数组,用于在迷宫中移动。
接下来,我们初始化 `visited` 数组,将其全部置为 `false`。
然后,将入口坐标 `start` 压入栈中。
在循环中,我们不断弹出栈顶元素,表示当前所在位置。如果当前位置是出口坐标 `end`,则表示找到了一条路径,循环结束,我们返回栈中的元素,即路径的顺序。
否则,我们将当前位置标记为已访问,并根据四个方向进行判断。对于每个方向,我们计算出相邻方块的坐标,如果该方块是通道且未访问过,则将其坐标压入栈中。
如果循环结束,栈为空,表示没有找到路径,我们返回 `null`。
示例用法展示了如何使用以上代码来找到从入口 `[0, 0]` 到出口 `[7, 7]` 的迷宫路径。
请注意,这只是一种基于栈的解法,可能存在多条从入口到出口的路径,该解法只返回其中一条路径。如果需要找到所有路径,可以使用递归或其他搜索算法。
**/
单调栈题集
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 0739 | 每日温度 | 栈、数组、单调栈 | 中等 |
| 0496 | 下一个更大元素 I | 栈、数组、哈希表、单调栈 | 简单 |
| 0503 | 下一个更大元素 II | 栈、数组、单调栈 | 中等 |
| 0901 | 股票价格跨度 | 栈、设计、数据流、单调栈 | 中等 |
| 0084 | 柱状图中最大的矩形 | 栈、数组、单调栈 | 困难 |
| 0316 | 去除重复字母 | 栈、贪心、字符串、单调栈 | 中等 |
| 0042 | 接雨水 | 栈、数组、双指针、动态规划、单调栈 | 困难 |
| 0085 | 最大矩形 | 栈、数组、动态规划、矩阵、单调栈 | 困难 |
| 0862 | 和至少为 K 的最短子数组 | 队列、数组、二分查找、前缀和、滑动窗口、单调队列、堆(优先队列) | 困难 |
下一个更大元素 I
题目
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
- 1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
示例 2:
输入:nums1 = [2,4], nums2 = [1,2,3,4].
输出:[3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 2 ,用加粗斜体标识,nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ,用加粗斜体标识,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。
提示:
1 <= nums1.length <= nums2.length <= 10000 <= nums1[i], nums2[i] <= 104nums1和nums2中所有整数 互不相同nums1中的所有整数同样出现在nums2中
解法一:暴力求解
- 遍历 𝑛𝑢𝑚𝑠1 中的每一个元素。
- 对于 𝑛𝑢𝑚𝑠1 的每一个元素 𝑛𝑢𝑚𝑠1[𝑖],再遍历一遍 𝑛𝑢𝑚𝑠2,查找 𝑛𝑢𝑚𝑠2 中对应位置右边第一个比 𝑛𝑢𝑚𝑠1[𝑖] 大的元素。
- 这种解法的时间复杂度是 𝑂(𝑛2)。
解法二:单调递增栈
- 因为 𝑛𝑢𝑚𝑠1 是 𝑛𝑢𝑚𝑠2 的子集,所以我们可以先遍历一遍 𝑛𝑢𝑚𝑠2,并构造单调递增栈,求出 𝑛𝑢𝑚𝑠2 中每个元素右侧下一个更大的元素。
- 然后将其存储到哈希表中。
- 然后再遍历一遍 𝑛𝑢𝑚𝑠1,从哈希表中取出对应结果,存放到答案数组中。
- 这种解法的时间复杂度是 𝑂(𝑛)。
具体做法如下:
- 使用数组 𝑟𝑒𝑠 存放答案。使用 𝑠𝑡𝑎𝑐𝑘 表示单调递增栈。使用哈希表 𝑛𝑢𝑚_𝑚𝑎𝑝 用于存储 𝑛𝑢𝑚𝑠2 中下一个比当前元素大的数值,映射关系为 当前元素值:下一个比当前元素大的数值。
- 遍历数组 𝑛𝑢𝑚𝑠2,对于当前元素:
- 如果当前元素值较小,则直接让当前元素值入栈。
- 如果当前元素值较大,则一直出栈,直到当前元素值小于栈顶元素。
- 出栈时,出栈元素是第一个大于当前元素值的元素。则将其映射到 𝑛𝑢𝑚_𝑚𝑎𝑝 中。
- 遍历完数组 𝑛𝑢𝑚𝑠2,建立好所有元素下一个更大元素的映射关系之后,再遍历数组 𝑛𝑢𝑚𝑠1。
- 从 𝑛𝑢𝑚_𝑚𝑎𝑝 中取出对应的值,将其加入到答案数组中。
- 最终输出答案数组 𝑟𝑒𝑠。
function nextGreaterElement(nums1, nums2) {
let res = []; // 存放结果
let stack = []; // 单调递增栈
let numMap = new Map(); // nums1中每个元素对应的单调递增栈
// 构造 nums2 的单调递增栈
for (let num of nums2) {
while (stack.length > 0 && num > stack[stack.length - 1]) {
// 栈中弹出的元素更小,num 即为栈中弹出元素的下一个更大元素
numMap.set(stack.pop(), num);
}
stack.push(num);
}
for (let num of nums1) {
res.push(numMap.has(num) ? numMap.get(num) : -1);
}
return res;
};
每日温度
题目
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
提示:
1 <= temperatures.length <= 10530 <= temperatures[i] <= 100
解法一:暴力求解
解法二:单调递增栈
- 首先,将答案数组 𝑎𝑛𝑠 全部赋值为 0。然后遍历数组每个位置元素。
- 如果栈为空,则将当前元素的下标入栈。
- 如果栈不为空,且当前数字大于栈顶元素对应数字,则栈顶元素出栈,并计算下标差。
- 此时当前元素就是栈顶元素的下一个更高值,将其下标差存入答案数组 𝑎𝑛𝑠 中保存起来,判断栈顶元素。
- 直到当前数字小于或等于栈顶元素,则停止出栈,将当前元素下标入栈。
- 最后输出答案数组 𝑎𝑛𝑠。
dailyTemperatures = function(T) {
const n = T.length;
const stack = [];
const ans = new Array(n).fill(0);
for (let i = 0; i < n; i++) {
//当前数字大于栈顶元素对应数字,则栈顶元素出栈,并计算下标差
while (stack.length > 0 && T[i] > T[stack[stack.length - 1]]) {
const index = stack.pop();
ans[index] = i - index;
}
//将当前元素的下标入栈
stack.push(i);
}
return ans;
};