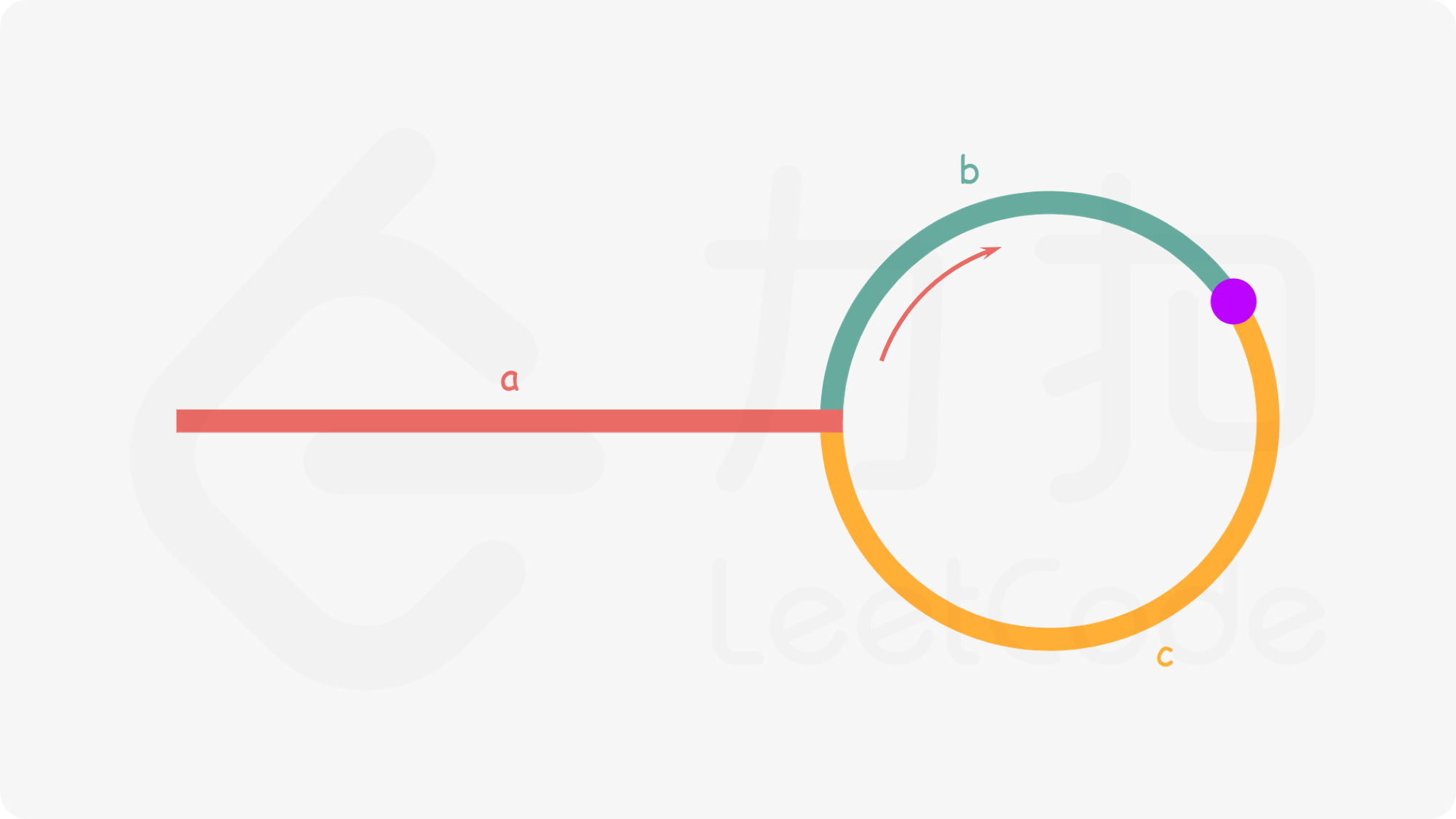链表
About 76 min
链表
概念
链表：
- 链表又称单链表、链式存储结构，用于存储逻辑关系为“一对一”的数据。
- 用一组任意存储的单元来存储线性表的数据元素。
- 一个对象存储着本身的值和下一个元素的地址。
节点：
- 在链表中，每个数据元素都配有一个指针；
- 数据域用来存储元素的值，指针域用来存放指针；
头结点、头指针和首元结点：
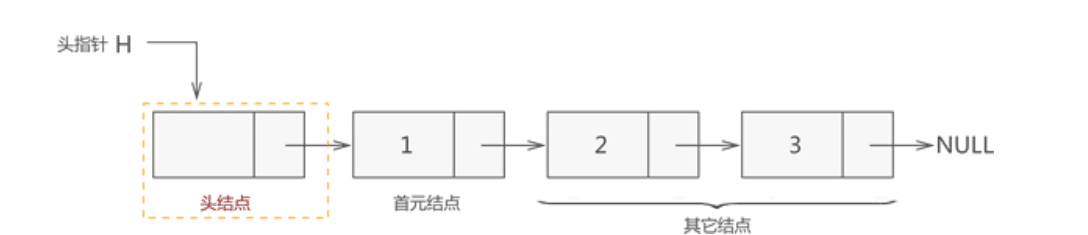
- 一个完整的链表应该由以下几部分构成
- 头指针：一个和结点类型相同的指针，它的特点是：永远指向链表中的第一个结点。上文提到过，我们需要记录链表中第一个元素的存储位置，就是用头指针实现。
- 结点：链表中的节点又细分为头结点、首元结点和其它结点：
- 头结点：某些场景中，为了方便解决问题，会故意在链表的开头放置一个空结点，这样的结点就称为头结点。也就是说，头结点是位于链表开头、数据域为空（不利用）的结点。
- 首元结点：指的是链表开头第一个存有数据的结点。
- 其他节点：链表中其他的节点。
- 一个完整的链表应该由以下几部分构成
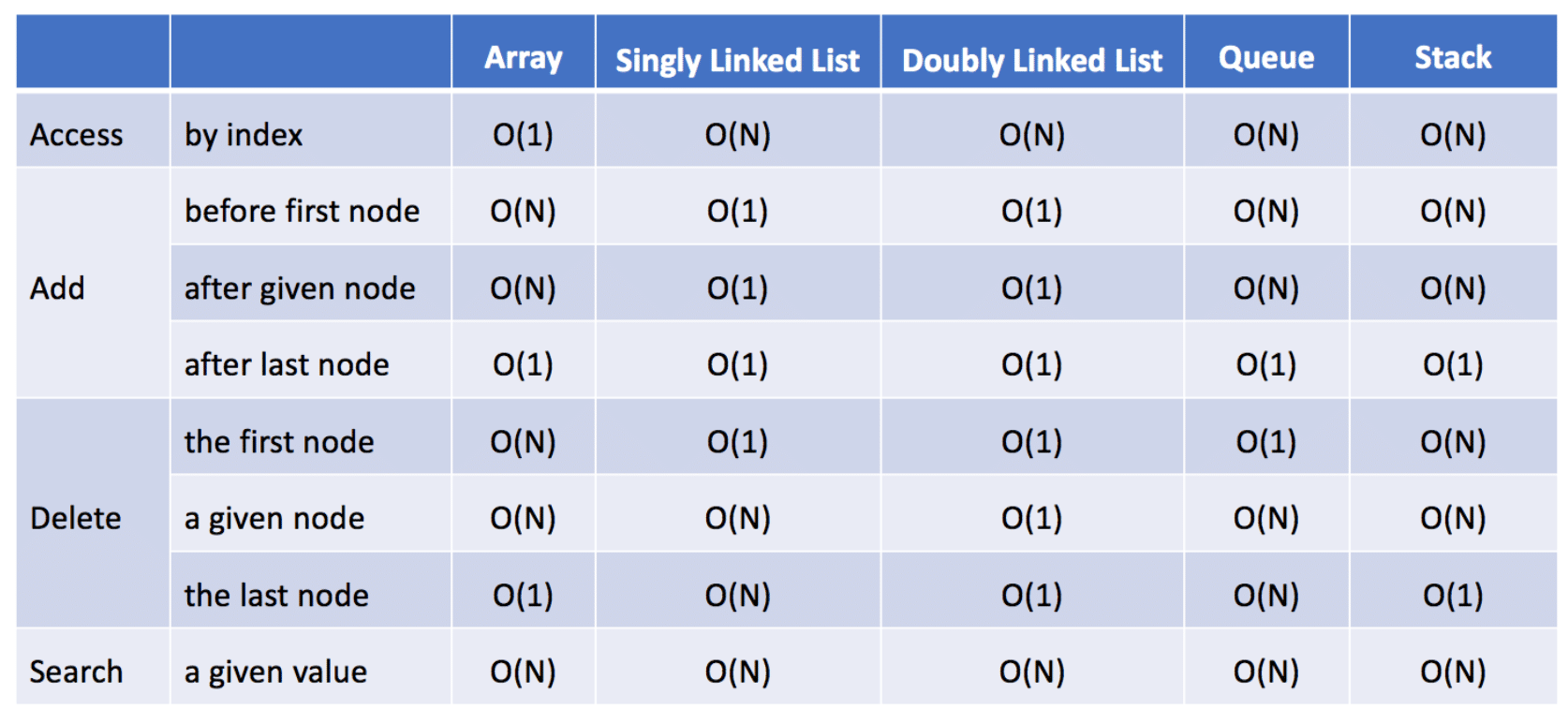
- 特点：
- 都无法在常量时间内随机访问数据。
- 能够在 O(1) 时间内在给定结点之后或列表开头添加一个新结点。
- 能够在 O(1) 时间内删除第一个结点。但是删除给定结点(包括最后一个结点)时略有不同。
- 在单链表中，它无法获取给定结点的前一个结点，因此在删除给定结点之前我们必须花费 O(N) 时间来找出前一结点。
- 在双链表中，删除更容易，因为我们可以使用“prev”引用字段获取前一个结点。因此我们可以在 O(1) 时间内删除给定结点。
分类
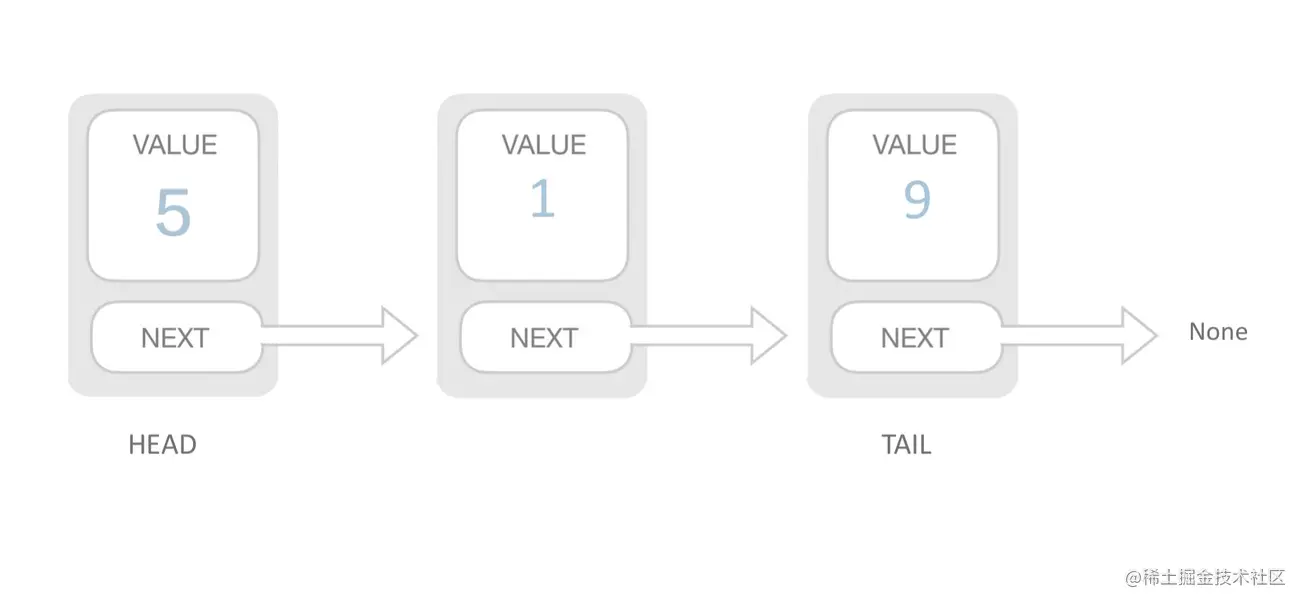
- 单向链表 (Singly Linked List):
- 单向链表是最简单和最常见的链表类型。
- 每个节点包含一个数据元素和一个指向下一个节点的指针。
- 从头节点开始，通过每个节点的指针可以按顺序遍历整个链表。
- 链表的尾节点的指针指向 null，表示链表的结束。
- 单向链表只能从头到尾进行遍历，不能逆向访问。
- 双向链表 (Doubly Linked List):
- 双向链表在单向链表的基础上扩展，每个节点除了包含数据元素和指向下一个节点的指针外，还包含一个指向前一个节点的指针。
- 双向链表可以从头到尾或从尾到头进行遍历，可以灵活地在链表中进行前后移动。
- 由于每个节点包含两个指针，相比单向链表，双向链表占用更多的内存空间。
- 循环链表 (Circular Linked List):
- 循环链表是一种特殊的链表，其尾节点的指针指向头节点，形成一个循环。
- 循环链表可以从任意节点开始遍历整个链表，直到回到起始节点。
- 循环链表常用于实现循环队列、循环缓冲区等数据结构。
- 带头节点的链表 (Linked List with Head Node):
- 带头节点的链表在链表的头部添加一个额外的头节点。
- 头节点不存储具体的数据，主要用于方便链表的操作和处理边界情况。
- 头节点的存在简化了对链表的操作，使得空链表和非空链表的处理方式一致。
- 带环链表 (Linked List with Cycle):
- 带环链表是一种具有环形结构的链表，其中至少存在一个节点的指针指向链表中的前面节点，形成一个环。
- 带环链表常用于解决相关问题，例如判断链表是否有环、找到环的起始点等。
单向链表
创建单向链表
创建不带头节点链表
思路一：不带尾指针的链表
- 定义一个头指针；
- 创建一个头结点或者首元结点，让头指针指向它；
- 每创建一个结点，都令其直接前驱结点的指针指向它。
代码:
class ListNode { constructor(value) { this.value = value; this.next = null; } } class LinkedList { constructor() { this.head = null; // 头指针 } insert(value) { // 创建新的节点 const newNode = new ListNode(value); // 判断链表是否为空，为空链接到 head 头指针后面 if (this.head === null) { this.head = newNode; } else { let currentNode = this.head; while (currentNode.next !== null) { //遍历移动到链表尾部 currentNode = currentNode.next; } currentNode.next = newNode; //新的节点插入链表尾部 } } print() { let currentNode = this.head; while (currentNode !== null) { console.log(currentNode.value); currentNode = currentNode.next; } } } // 示例用法 const linkedList = new LinkedList(); linkedList.insert(1); linkedList.insert(2); linkedList.insert(3); linkedList.insert(4); linkedList.print(); // 输出链表的值思路二：带尾指针的链表
- 定义一个头指针和一个尾指针；
- 创建一个头结点或者首元结点，让头指针和尾指针都指向它；
- 每创建一个结点，都令其直接前驱结点的指针指向它。
代码：
class ListNode { constructor(value) { this.value = value; this.next = null; } } class LinkedList { constructor() { this.head = null; // 头指针 this.tail = null; // 尾指针 } insert(value) { // 创建新的节点 const newNode = new ListNode(value); // 判断链表是否为空，为空链接到 head 头指针后面 if (this.head === null) { this.head = this.tail = newNode; } else { this.tail.next = newNode; this.tail = newNode; } } print() { let currentNode = this.head; while (currentNode !== null) { console.log(currentNode.value); currentNode = currentNode.next; } } } // 示例用法 const linkedList = new LinkedList(); linkedList.insert(1); linkedList.insert(2); linkedList.insert(3); linkedList.insert(4); linkedList.print(); // 输出链表的值
创建带头节点链表
代码
class ListNode { constructor(value) { this.value = value; this.next = null; } } class LinkedList { constructor() { this.head = new ListNode(null); // 头节点 } insert(value) { const newNode = new ListNode(value); let currentNode = this.head; while (currentNode.next !== null) { currentNode = currentNode.next; } currentNode.next = newNode; } print() { let currentNode = this.head.next; while (currentNode !== null) { console.log(currentNode.value); currentNode = currentNode.next; } } } // 示例用法 const linkedList = new LinkedList(); linkedList.insert(1); linkedList.insert(2); linkedList.insert(3); linkedList.insert(4); linkedList.print(); // 输出链表的值
输入一组数据创建链表
思路：
首先定义了一个
ListNode类来表示链表的节点。节点对象有一个value属性用于存储节点的值，以及一个next属性用于指向下一个节点。然后，定义了一个名为
createLinkedList的函数，它接受一个数组arr作为参数，用于创建链表。如果传入的数组是空数组，则返回null表示空链表。在
createLinkedList函数中，首先根据数组的第一个元素创建链表的头节点head，然后使用一个循环遍历数组的剩余元素。在循环中，每次创建一个新的节点newNode，并将当前节点currentNode的next属性指向新节点，然后更新currentNode为新节点，以便下一次循环连接下一个节点。最后，返回链表的头节点
head。
代码：
// 使用类构造链表结构 class ListNode { constructor(value) { this.value = value; //保存链表的值 this.next = null; // 保存链表下一个值 } } // 创建链表函数 function createLinkedList(arr) { if (arr.length === 0) { // 判断数据为空，返回 Null return null; } // 创建链表头节点 const head = new ListNode(arr[0]); let currentNode = head; // 链表创建指针 // 循环创建链表 for (let i = 1; i < arr.length; i++) { const newNode = new ListNode(arr[i]); // 创建链表节点 currentNode.next = newNode; // 链表指针节点指向新节点 currentNode = newNode; // 指针指向新节点 } return head; //返回头指针 } // 示例用法 const arr = [1, 2, 3, 4, 5]; const linkedList = createLinkedList(arr); // 打印链表的值 let currentNode = linkedList; while (currentNode !== null) { //最后一个节点 next 为空，因此打印边界判断为 next 是否空 console.log(currentNode.value); currentNode = currentNode.next; }
链表插入
链表插入可以分为两种：
- 带头节点的链表的插入，插入任何一个位置操作都相同；
- 不带头节点的链表插入，要区分插入头节点位置和其他位置两种情况；
向链表中增添元素，根据添加位置不同，可分为以下 3 种情况：
插入到链表的头部，作为首元节点；
插入到链表中间的某个位置；
插入到链表的最末端，作为链表中最后一个结点；
有头节点链表插入
思路：
对于有头结点的链表，3 种插入元素的实现思想是相同的，具体步骤是：（注意：第二步和第三步不能交换）
- 遍历查找到要插入位置的前一个节点；
- 将新结点的 next 指针指向插入位置后的结点；
- 将插入位置前结点的 next 指针指向插入结点；
例如，在链表
{1,2,3,4}的基础上分别实现在头部、中间、尾部插入新元素 5，其实现过程如：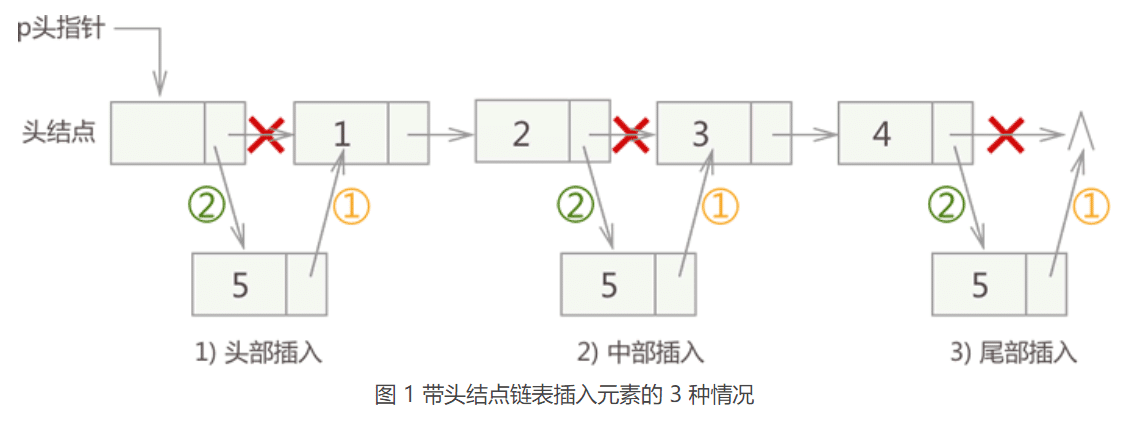
代码
// 链表结构 class ListNode { constructor(value) { this.value = value; this.next = null; } } class LinkedList { constructor() { this.head = new ListNode(null); // 头节点 } // 插入头部 insertAtHead(value) { const newNode = new ListNode(value); newNode.next = this.head.next; // 将新节点的 next 指向原来的第一个节点 this.head.next = newNode; // 更新头节点的 next 指向新节点 } /** * 插入任意位置 * params { int } position 插入位置 * params { int } value 插入值 **/ insertAtPosition(position, value) { if (position <= 0) { console.log("Invalid position."); return false; } let count = 0; // 位置计数器 let currentNode = this.head; // 遍历找到插入位置的前一个节点 while (currentNode !== null && count < position - 1) { currentNode = currentNode.next; count++; } if (currentNode === null) { console.log("Invalid position."); return; } //创建新的节点 const newNode = new ListNode(value); newNode.next = currentNode.next; // 将新节点的 next 指向插入位置后的节点 currentNode.next = newNode; // 更新插入位置前节点的 next 指向新节点 } // 插入末尾 insertAtEnd(value) { let currentNode = this.head; // 遍历找到尾节点 while (currentNode.next !== null) { currentNode = currentNode.next; } // 插入尾节点 const newNode = new ListNode(value); currentNode.next = newNode; // 将新节点连接到链表末尾 } print() { let currentNode = this.head.next; // 跳过头节点 while (currentNode !== null) { console.log(currentNode.value); currentNode = currentNode.next; } } } // 示例用法 const linkedList = new LinkedList(); linkedList.insertAtHead(3); linkedList.insertAtHead(2); linkedList.insertAtHead(1); linkedList.print(); // 输出链表的值 console.log('---'); linkedList.insertAtPosition(2, 4); linkedList.print(); // 输出插入到中间位置后的链表的值 console.log('---'); linkedList.insertAtEnd(5); linkedList.print(); // 输出插入到末尾后的链表的值
无头节点链表插入
思路：
对于没有头结点的链表，在头部插入结点比较特殊，需要单独实现：因此需要分两种情况：
头部插入新结点：
- 将新结点的指针指向首元结点；
- 将头指针指向新结点。
非头部节点插入新节点：
- 遍历查找到要插入位置的前一个节点；
- 将新结点的 next 指针指向插入位置后的结点；
- 将插入位置前结点的 next 指针指向插入结点；
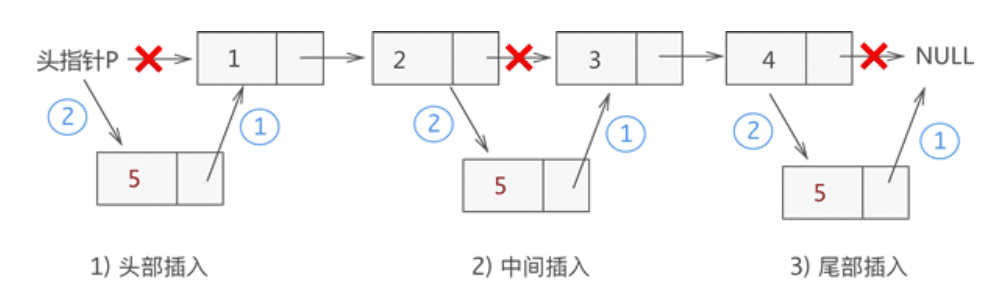
代码：
class ListNode { constructor(value) { this.value = value; this.next = null; } } class LinkedList { constructor() { this.head = null; // 头指针 } // 插入头节点 insertAtHead(value) { const newNode = new ListNode(value); newNode.next = this.head; // 将新节点的 next 指向首元节点 this.head = newNode; // 更新头指针指向新节点 } /** * 插入任意位置 * params { int } position 插入位置 * params { int } value 插入值 **/ insertAtPosition(position, value) { if (position <= 0) { console.log("Invalid position."); return; } let count = 0; let currentNode = this.head; let previousNode = null; // 插入位置节点前节点指针 while (currentNode !== null && count < position) { previousNode = currentNode; // 当前节点作为前一个节点 currentNode = currentNode.next; // 指针后移 count++; } if (count < position) { console.log("Invalid position."); return; } const newNode = new ListNode(value); newNode.next = currentNode; // 将新节点的 next 指向插入位置后的节点 if (previousNode === null) { this.head = newNode; // 如果是在头部插入，更新头指针指向新节点 } else { previousNode.next = newNode; // 更新插入位置前节点的 next 指向新节点 } } print() { let currentNode = this.head; while (currentNode !== null) { console.log(currentNode.value); currentNode = currentNode.next; } } } // 示例用法 const linkedList = new LinkedList(); linkedList.insertAtHead(3); linkedList.insertAtHead(2); linkedList.insertAtHead(1); linkedList.print(); // 输出链表的值 console.log('---'); linkedList.insertAtPosition(2, 4); linkedList.print(); // 输出插入到中间位置后的链表的值 console.log('---'); linkedList.insertAtHead(0); linkedList.print(); // 输出头部插入后的链表的值
链表删除
- 链表删除可以分为两种：
- 带头节点的链表的删除，插入任何一个位置操作都相同；
- 不带头节点的链表删除，要区分插入头节点位置和其他位置两种情况；
有头节点的链表删除
思路：
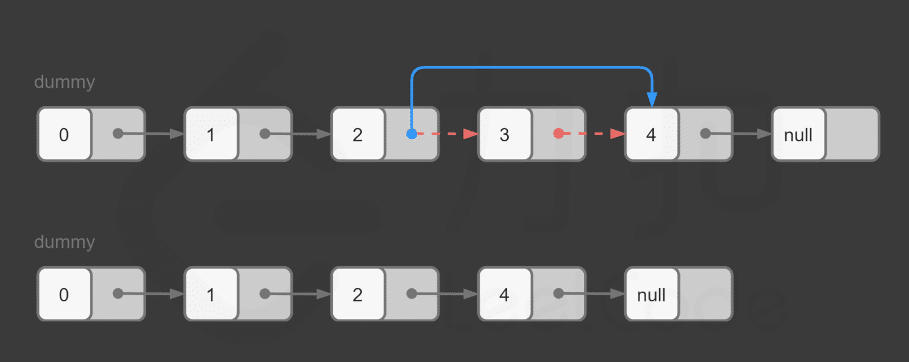
对于有头结点的链表来说，无论删除头部（首元结点）、中部、尾部的结点，实现方式都一样，执行以下三步操作：
- 找到目标元素所在结点的直接前驱结点；
- 将目标结点从链表中摘下来;
- 手动释放结点占用的内存空间；
从链表上摘除目标节点，只需找到该节点的直接前驱节点 temp，执行如下操作：
temp->next=temp->next->next;
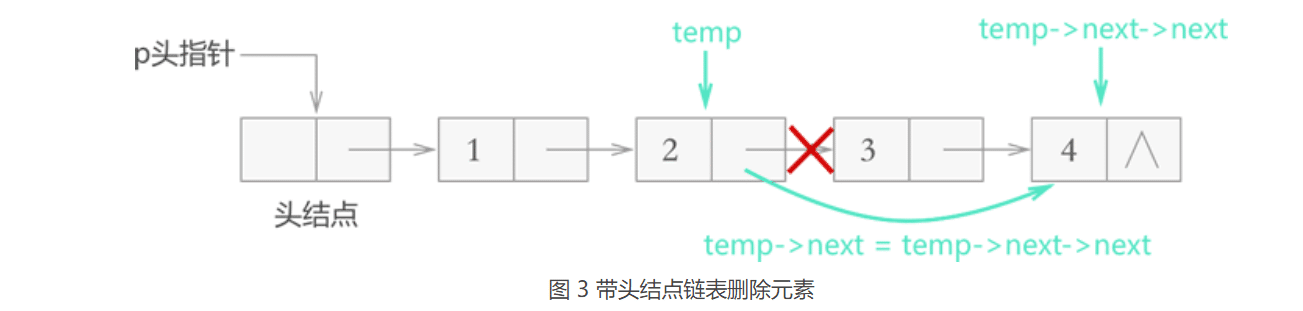
代码：
class ListNode { constructor(value) { this.value = value; this.next = null; } } class LinkedList { constructor() { this.head = new ListNode(null); // 头节点 } // 链表尾部插入节点，用于构建链表 insert(value) { const newNode = new ListNode(value); let currentNode = this.head; while (currentNode.next !== null) { currentNode = currentNode.next; } currentNode.next = newNode; } // 删除节点 delete(value) { let currentNode = this.head; let previousNode = null; // 删除元素的前一个元素指针 // 循环查找到待删除的节点 while (currentNode !== null && currentNode.value !== value) { previousNode = currentNode; currentNode = currentNode.next; } if (currentNode === null) { console.log("Element not found."); return; } // 重点：删除节点，通过将待删除节点和后一个节点连接删除 previousNode.next = currentNode.next; currentNode.next = null; delete currentNode; } print() { let currentNode = this.head.next; while (currentNode !== null) { console.log(currentNode.value); currentNode = currentNode.next; } } } // 示例用法 const linkedList = new LinkedList(); linkedList.insert(1); linkedList.insert(2); linkedList.insert(3); linkedList.insert(4); linkedList.print(); // 输出链表的值 console.log('---'); linkedList.delete(3); linkedList.print(); // 输出删除节点后的链表的值
无头节点的链表删除
思路：
对于不带头结点的链表，需要单独考虑删除首元结点的情况，删除其它结点的方式带头节点方式完全相同；
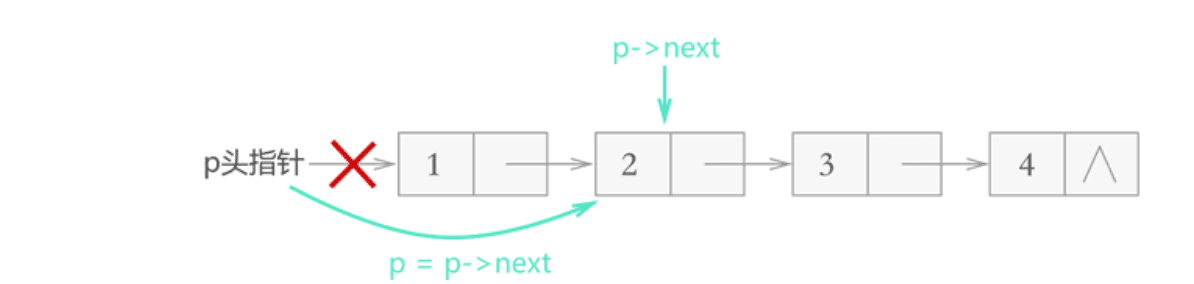
删除首元节点时，直接改变头指针位置；
删除非首元节点时，遍历查找节点位置，再链接删除节点的前一个节点和后一个节点；
代码：
class ListNode { constructor(value) { this.value = value; this.next = null; } } class LinkedList { constructor() { this.head = null; // 头指针 } insert(value) { const newNode = new ListNode(value); if (this.head === null) { this.head = newNode; } else { let currentNode = this.head; // 移动到链表尾部 while (currentNode.next !== null) { currentNode = currentNode.next; } // 节点加入链表的尾部 currentNode.next = newNode; } } delete(value) { if (this.head === null) { console.log("Empty list."); return; } if (this.head.value === value) { this.head = this.head.next; //删除头节点元素 return; } // 当前节点元素指针 let currentNode = this.head; let previousNode = null; // 当前节点元素前一个节点指针 // 查找元素内容 while (currentNode !== null && currentNode.value !== value) { previousNode = currentNode; // 当前直接变为前一个节点 currentNode = currentNode.next; // 当前节点指针后移 } if (currentNode === null) { console.log("Element not found."); return; } // 重点：删除元素节点，链接删除元素的前一个节点和后一个节点 previousNode.next = currentNode.next; currentNode.next = null; delete currentNode; } print() { let currentNode = this.head; while (currentNode !== null) { console.log(currentNode.value); currentNode = currentNode.next; } } } // 示例用法 const linkedList = new LinkedList(); linkedList.insert(1); linkedList.insert(2); linkedList.insert(3); linkedList.insert(4); linkedList.print(); // 输出链表的值 console.log('---'); linkedList.delete(3); linkedList.print(); // 输出删除节点后的链表的值
删除链表重复节点
思路：
- 1.用一个map存储每个节点出现的次数
- 2.删除出现次数大于1的节点:
- 1.删除的节点不是尾部节点 - 将next节点覆盖当前节点；
- 2.删除的节点是尾部节点且等于头节点，只剩一个节点 - 将头节点置为 null；
- 3.删除的节点是尾节点且前面还有节点 - 遍历到末尾的前一个节点删除；
时间复杂度：O(n)；空间复杂度：O(n)；
代码：
function deleteDuplication(pHead) { const map = {}; // 如果链表不为空 if (pHead && pHead.next) { let current = pHead; // 计算每个节点出现次数 while (current) { const val = map[current.val]; map[current.val] = val ? val + 1 : 1; current = current.next; } // 重新指向头节点开始遍历 current = pHead; while (current) { const val = map[current.val];//获取当前遍历节点的出现次数 if (val > 1) { //出现次数大于一，删除当前节点 // 删除的节点不是尾部节点,将next节点覆盖当前节点 if (current.next) { current.val = current.next.val; current.next = current.next.next; // 删除的节点是尾部节点且等于头节点，只剩一个节点,将头节点置为 null； } else if (current === pHead) { current = null; pHead = null; } else { // 删除的节点是尾节点且前面还有节点,遍历到末尾的前一个节点删除； current = pHead; while (current.next.next) { current = current.next; } current.next = null; current = null; } } else { current = current.next; } } } return pHead; }
从尾到头打印链表
题目：
输入一个链表，按链表值从尾到头的顺序返回一个
ArrayList。思路：
要了解链表的数据结构：
val属性存储当前的值，next属性存储下一个节点的引用。要遍历链表就是不断找到当前节点的
next节点，当next节点是null时，说明是最后一个节点，停止遍历。因为是从尾到头的顺序，使用一个队列来存储打印结果，每次从队列头部插入。
代码：
/*function ListNode(x){ this.val = x; this.next = null; }*/ function printListFromTailToHead(head) { const array = []; while(head){ array.unshift(head.val); //将元素移入队列头部 head = head.next; } return array; }
反转链表
题目：
输入一个链表，反转链表后，输出新链表的表头。
方法一：重建链表
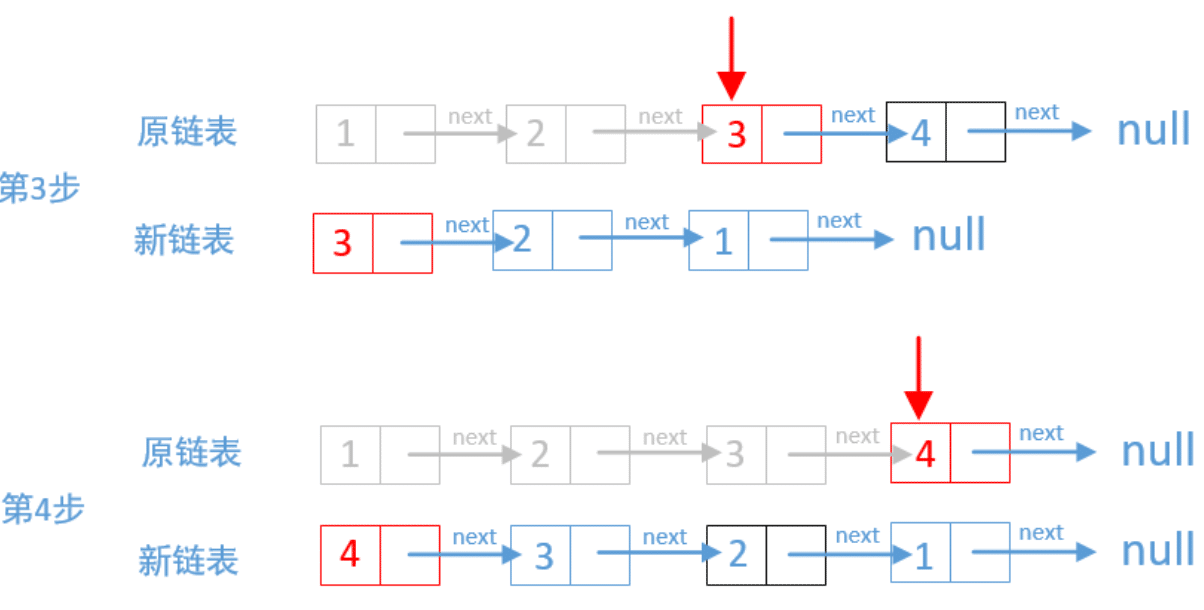
以链表的头部节点为基准节点
将基准节点的下一个节点挪到头部作为头节点
当基准节点的
next为null，则其已经成为最后一个节点，链表已经反转完成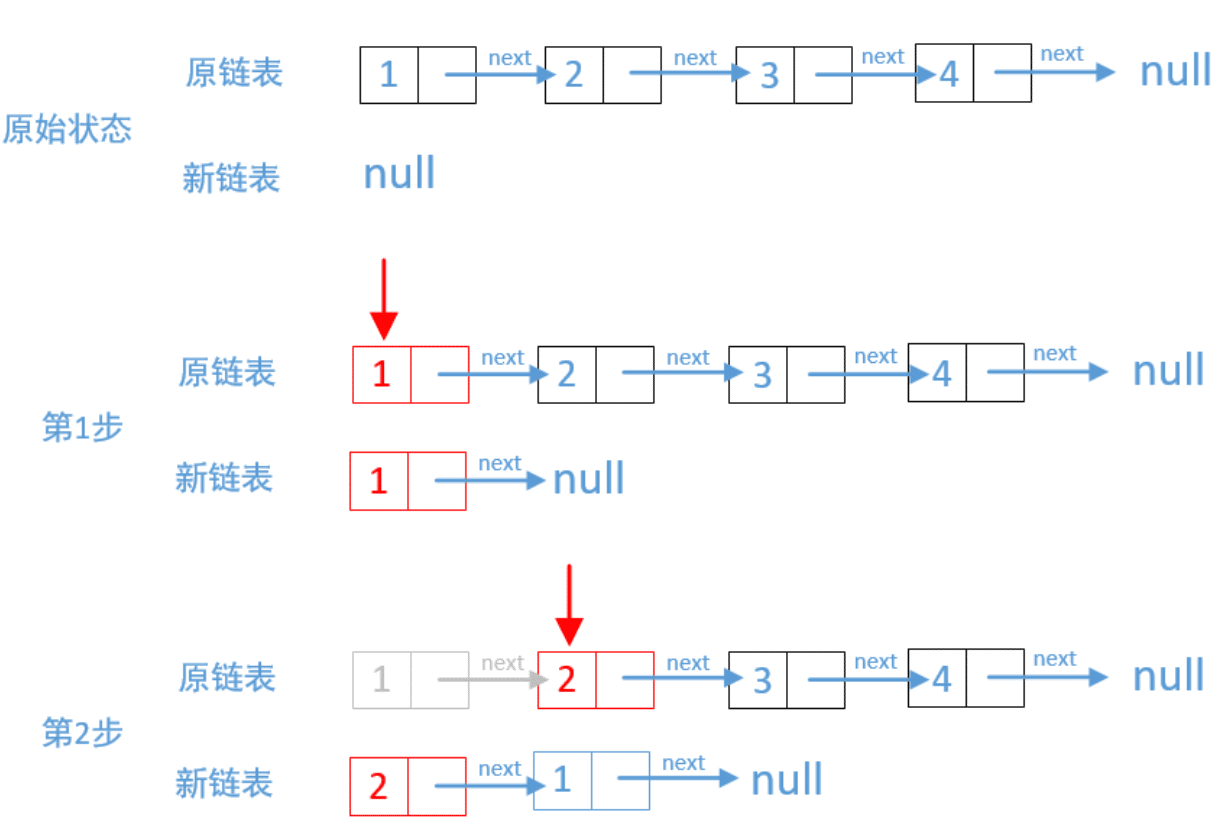
代码：
var reverseList = function (head) { let currentNode = null; let headNode = head;//以链表的头部节点为基准节点 while (head && head.next) {//遍历链表 currentNode = head.next; // 头部下一个节点 head.next = currentNode.next; // 链接头部节点和下下一个结点 currentNode.next = headNode;//头部下一个节点链接头部 headNode = currentNode; } return headNode; };
方法二：栈
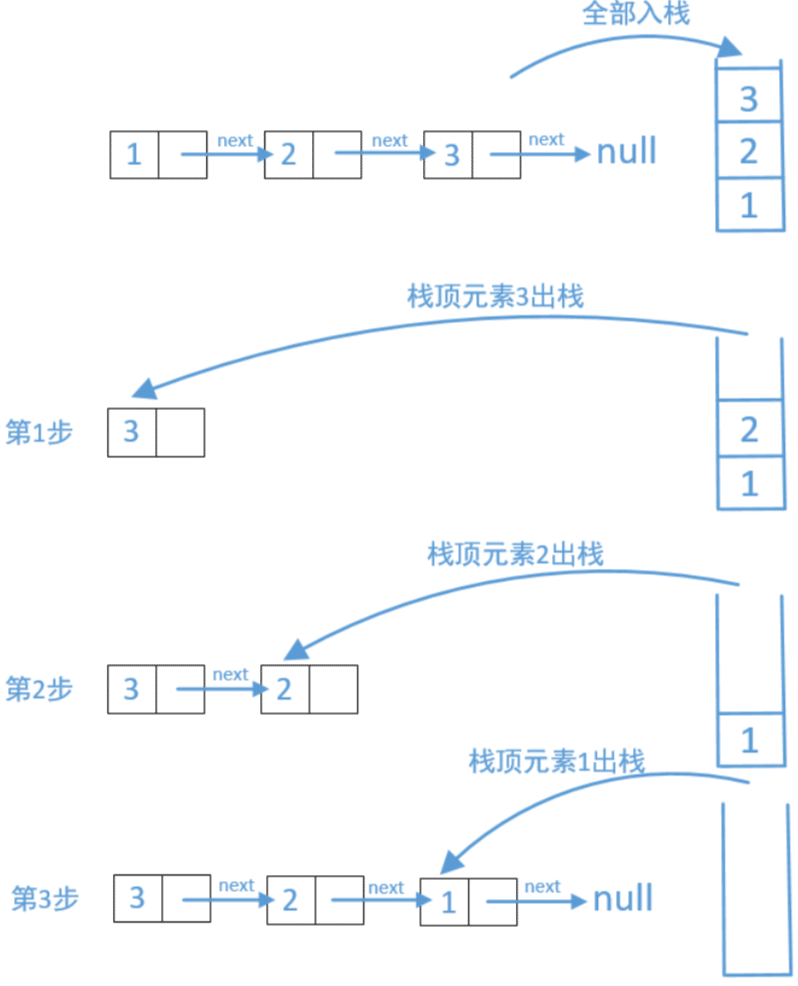
利用栈 "先进后出" 特点：
遍历链表，将节点入栈；
遍历结束后，将栈元素逐个出栈，并将元素链接起来；
代码：
/** * Definition for singly-linked list. * function ListNode(val, next) { * this.val = (val===undefined ? 0 : val) * this.next = (next===undefined ? null : next) * } */ /** * @param {ListNode} head * @return {ListNode} */ var reverseList = function(head) { let stack = []; let curNode = head; while(curNode) { stack.push(curNode); curNode = curNode.next; } if(stack.length === 0) return null; head = curNode = stack.pop(); // 将头节点出栈 let len = stack.length; // 注意：此处重新计算栈长度，在出栈时，栈长度会改变，需要使用新的变量保存 let temp = null; for(let i=0; i< len; i++) { temp = stack.pop(); temp.next = null; curNode.next = temp; curNode = temp; } return head; };方法三：递归
- 首先，判断链表是否为空或只有一个节点，如果是，则直接返回当前节点作为反转后的链表的表头。
- 如果链表有两个或更多节点，我们可以将链表分为两部分：头节点和剩余部分。假设剩余部分已经被反转，我们需要将头节点放置在剩余部分反转后的最后一个节点的后面。
- 为了实现这一点，我们需要将剩余部分的最后一个节点的下一个节点设置为头节点，并将头节点的下一个节点设为 null，以断开原来的连接。
- 最后，我们将原链表的剩余部分反转得到的链表的表头连接到头节点后面，并返回新的表头。
代码:
class ListNode { constructor(val, next = null) { this.val = val; this.next = next; } } function reverseList(head) { // 链表为空或只有一个节点，直接返回当前节点 if (!head || !head.next) { return head; } // 反转剩余部分 const newHead = reverseList(head.next); // 将头节点放置在剩余部分反转后的最后一个节点的后面 head.next.next = head; head.next = null; return newHead; } // 示例用法 // 创建一个链表：1 -> 2 -> 3 -> 4 -> 5 const node1 = new ListNode(1); const node2 = new ListNode(2); const node3 = new ListNode(3); const node4 = new ListNode(4); const node5 = new ListNode(5); node1.next = node2; node2.next = node3; node3.next = node4; node4.next = node5; const reversedHead = reverseList(node1); console.log(reversedHead); // 输出反转后链表的表头
奇偶链表
题目：
给定单链表的头节点 head ，将所有索引为奇数的节点和索引为偶数的节点分别组合在一起，然后返回重新排序的列表。
第一个节点的索引被认为是 奇数 ， 第二个节点的索引为 偶数 ，以此类推。
请注意，偶数组和奇数组内部的相对顺序应该与输入时保持一致。
你必须在 O(1) 的额外空间复杂度和 O(n) 的时间复杂度下解决这个问题。
示例:
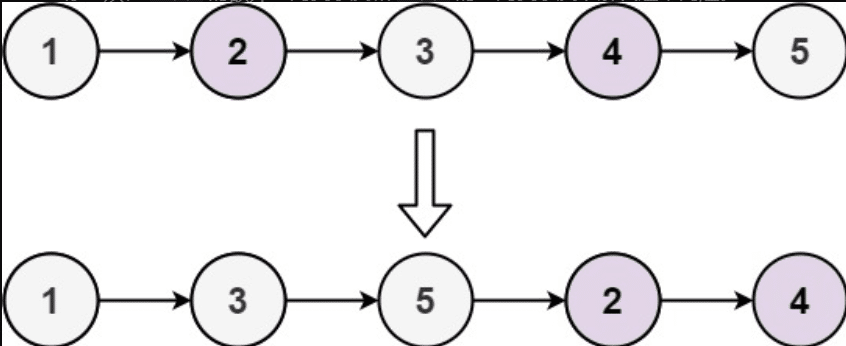
输入: head = [1,2,3,4,5] 输出: [1,3,5,2,4]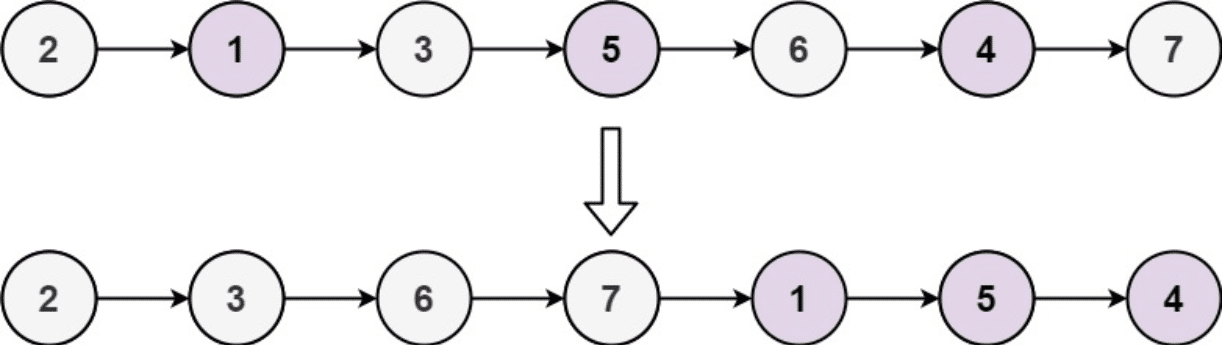
输入: head = [2,1,3,5,6,4,7] 输出: [2,3,6,7,1,5,4]
思路：分离节点后合并
如果链表为空，则直接返回链表。
对于原始链表，每个节点都是奇数节点或偶数节点。头节点是奇数节点，头节点的后一个节点是偶数节点，相邻节点的奇偶性不同。因此可以将奇数节点和偶数节点分离成奇数链表和偶数链表，然后将偶数链表连接在奇数链表之后，合并后的链表即为结果链表。
原始链表的头节点 head 也是奇数链表的头节点以及结果链表的头节点，head 的后一个节点是偶数链表的头节点。令 evenHead = head.next，则 evenHead 是偶数链表的头节点。
维护两个指针 odd 和 even 分别指向奇数节点和偶数节点，初始时 odd = head，even = evenHead。通过迭代的方式将奇数节点和偶数节点分离成两个链表，每一步首先更新奇数节点，然后更新偶数节点。
- 更新奇数节点时，奇数节点的后一个节点需要指向偶数节点的后一个节点，因此令 odd.next = even.next，然后令 odd = odd.next，此时 odd 变成 even 的后一个节点。
- 更新偶数节点时，偶数节点的后一个节点需要指向奇数节点的后一个节点，因此令 even.next = odd.next，然后令 even = even.next，此时 even 变成 odd 的后一个节点。
在上述操作之后，即完成了对一个奇数节点和一个偶数节点的分离。
重复上述操作，直到全部节点分离完毕。全部节点分离完毕的条件是 even 为空节点或者 even.next 为空节点，此时 odd 指向最后一个奇数节点（即奇数链表的最后一个节点）。
最后令 odd.next = evenHead，将偶数链表连接在奇数链表之后，即完成了奇数链表和偶数链表的合并，结果链表的头节点仍然是 head。
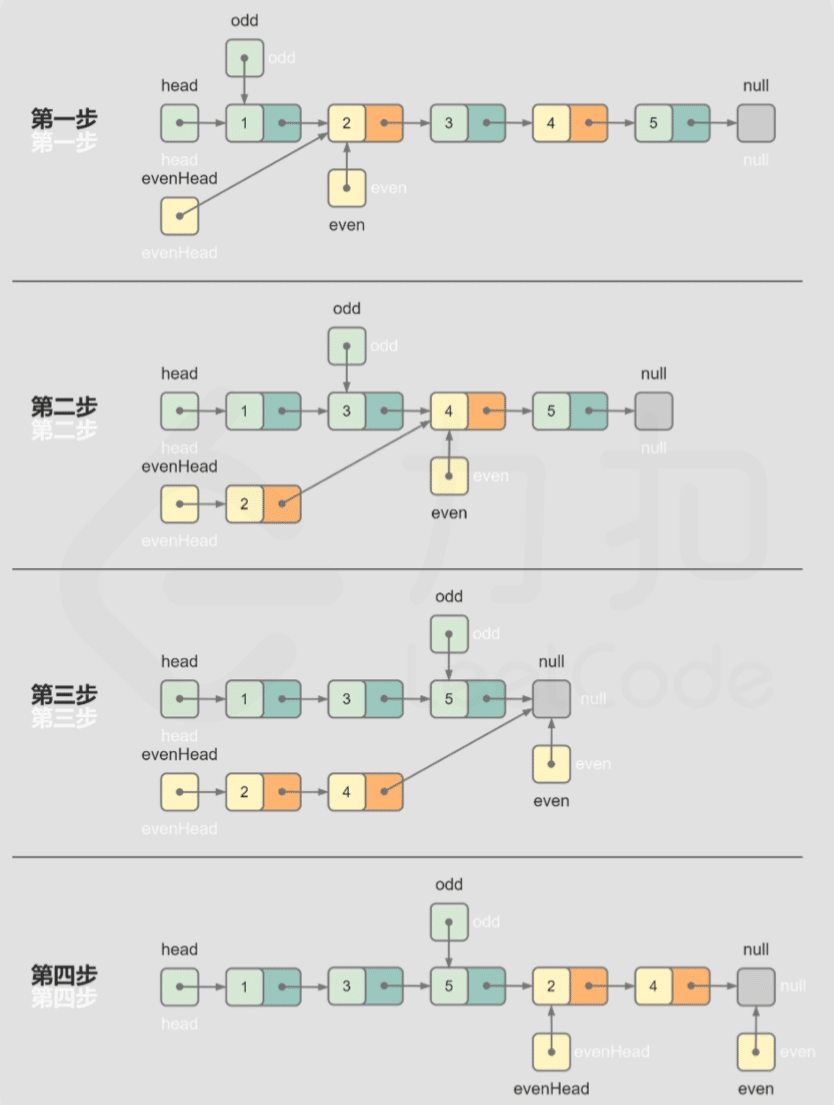
代码：
var oddEvenList = function(head) { if (head === null) { return head; } let evenHead = head.next; // 奇数指针指向第一个节点，偶数指针指向奇数指针节点的下一个节点 let odd = head, even = evenHead; // 偶数指针指向最后一个节点时，推出循环 while (even !== null && even.next !== null) { odd.next = even.next; // 将偶数指针节点链接到奇数指针节点的 next，则奇数节点相连接 odd = odd.next; // 奇数指针后移到下一个奇数节点 even.next = odd.next; // 将奇数指针节点链接到偶数指针节点的 next，则偶数节点相连接 even = even.next;// 偶数指针后移到下一个偶数节点 } odd.next = evenHead; // 此时奇数指针指向最后一个奇数节点，将最后一个奇数节点与偶数链表头节点链接 return head; };
回文链表
题目：
给你一个单链表的头节点 head ，请你判断该链表是否为回文链表（回文数字是指从左到右和从右到左读取都相同的数字，例如，121、12321和1221都是回文数字）。
如果是，返回 true ；否则，返回 false 。
示例 1：
输入：head = [1,2,2,1] 输出：true示例 2：
输入：head = [1,2] 输出：false提示：
链表中节点数目在范围[1, 105] 内 0 <= Node.val <= 9进阶：你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？
解法一：使用栈和遍历
- 思想：将链表中间拆开两部分进行比较，并且利用栈的”先进后出“ 特性, 逆序前半部分链表节点；
- 首次遍历链表，获取链表长度 len；
- 根据链表长度，获取遍历链表 head 节点到 Math.floor(len/2) 长度的节点，将节点入栈；
- 判断 len 是奇数还是偶数：
- len%2 != 0，表示链表长度为奇数，要跳过中间节点；
- 继续遍历链表剩余节点，并将剩余节点的值与栈中的数据对比，将节点出栈，并判断当前出栈元素值是否等于链表当前遍历的节点值：
- 如果相等，链表指针后移；
- 如果不相等，返回 false;
- 遍历结束，说明栈中元素等于后半部分元素。
- 时间复杂度 O(n)，空间复杂度 O(n);
代码：
/** * Definition for singly-linked list. * function ListNode(val, next) { * this.val = (val===undefined ? 0 : val) * this.next = (next===undefined ? null : next) * } */ /** * @param {ListNode} head * @return {boolean} */ var isPalindrome = function(head) { let len = 0; let curNode = head; let stack = []; // 只有一个节点，为回文链表 if(!head.next) return true; // 统计链表长度 while(curNode) { len ++; curNode = curNode.next; } curNode = head; // 遍历链表前半部分，将所有节点入栈，形成逆序顺序(注意长度向下取整数) for(let i=0; i<Math.floor(len/2); i++) { stack.push(curNode); curNode = curNode.next; } // 链表长度为奇数，跳过中间节点 if(len %2 !=0) { curNode=curNode.next; } // 遍历链表后半部分，并与栈中节点值对比 while(curNode) { let top = stack.pop(); // 栈中节点值不等于后半部分链表值，不是回文链表 if(curNode.val !== top.val) { return false; }else { curNode = curNode.next; } } return true; };
- 思想：将链表中间拆开两部分进行比较，并且利用栈的”先进后出“ 特性, 逆序前半部分链表节点；
解法二：将值复制到数组中后用双指针法
复制链表值到数组列表中:
使用双指针法判断是否为回文。
- 在起点放置一个指针，在结尾放置一个指针，每一次迭代判断两个指针指向的元素是否相同:
- 若不同，返回 false；
- 相同则将两个指针向内移动，并继续判断，直到两个指针相遇。
- 在起点放置一个指针，在结尾放置一个指针，每一次迭代判断两个指针指向的元素是否相同:
时间复杂度：O(n)，其中 n 指的是链表的元素个数。
- 第一步： 遍历链表并将值复制到数组中，O(n)。
- 第二步：双指针判断是否为回文，执行了 O(n/2) 次的判断，即 O(n)。
- 总的时间复杂度：O(2n)=O(n)。
空间复杂度：O(n)，其中 n 指的是链表的元素个数，我们使用了一个数组列表存放链表的元素值。
代码：
var isPalindrome = function(head) { const vals = []; while (head !== null) { vals.push(head.val); head = head.next; } for (let i = 0, j = vals.length - 1; i < j; ++i, --j) { if (vals[i] !== vals[j]) { return false; } } return true; };
解法三：递归
设立一个指针 currentNode，从链表头节点开始递归遍历尾节点，只要存在节点就往下递归 currentNode 指向下一个节点；
当 currentNode 递归到最后一个节点后，由于递归的特性，当递归函数返回时，currentNode 将会从后往前进行比较：
使用函数外的指针 frontPointer 一直指向链表头
若 currentNode.val != frontPointer.val 则返回 false。
反之，frontPointer 向前移动并返回 true。
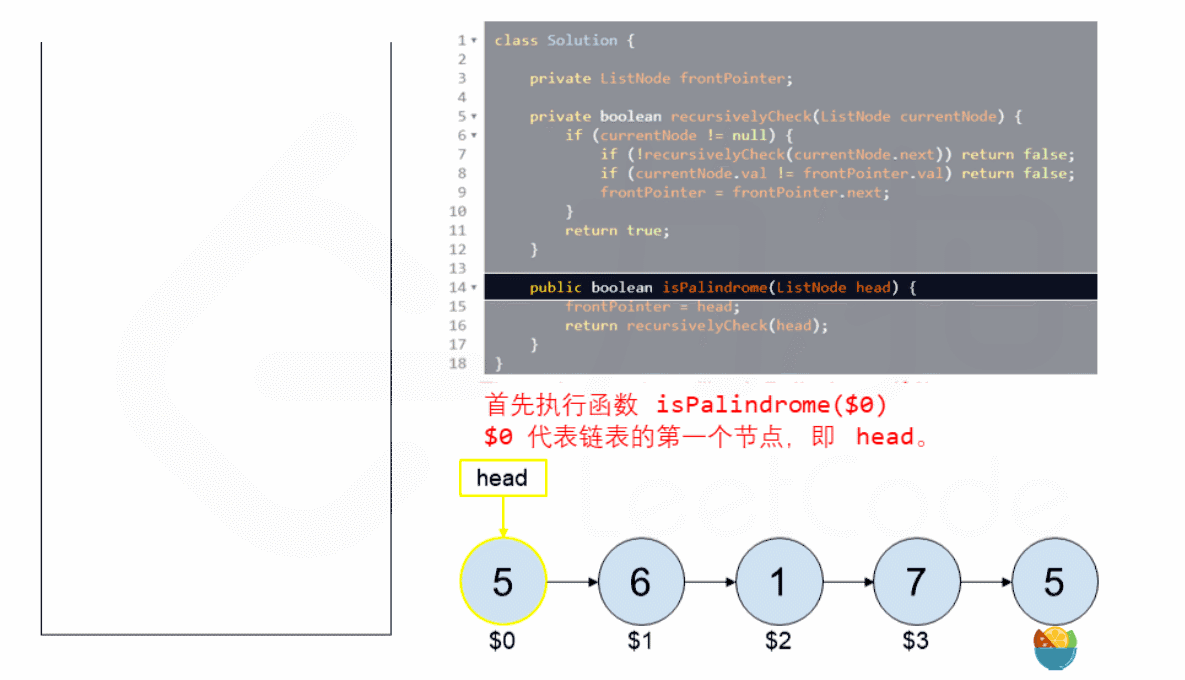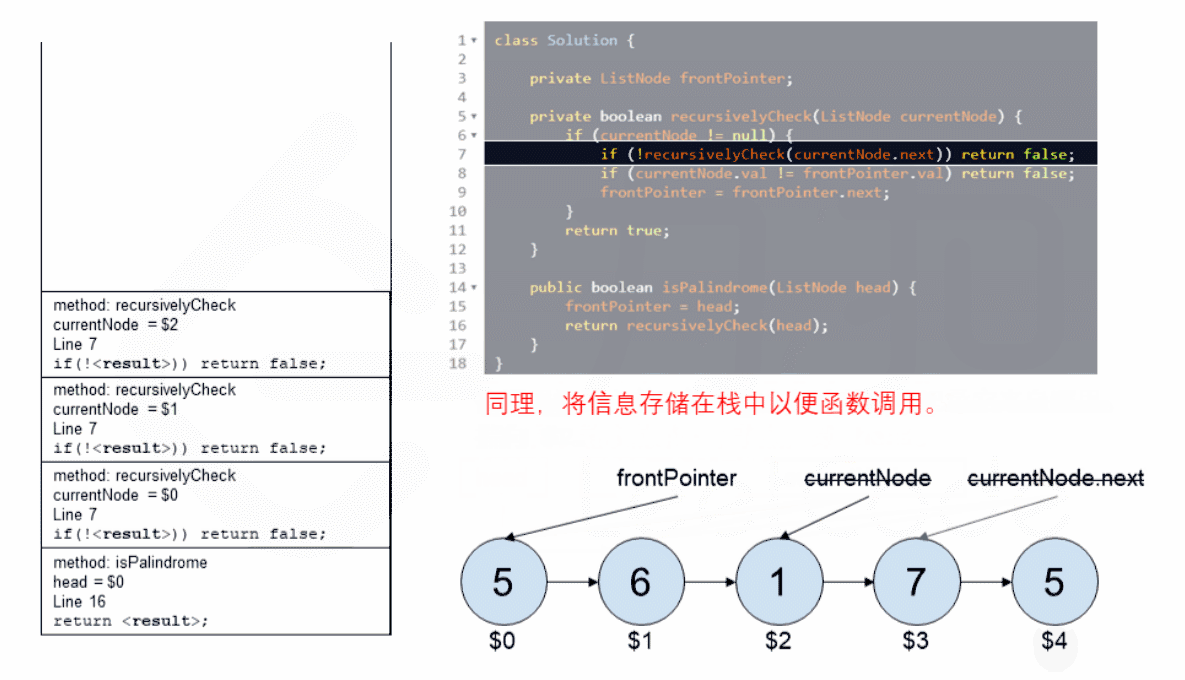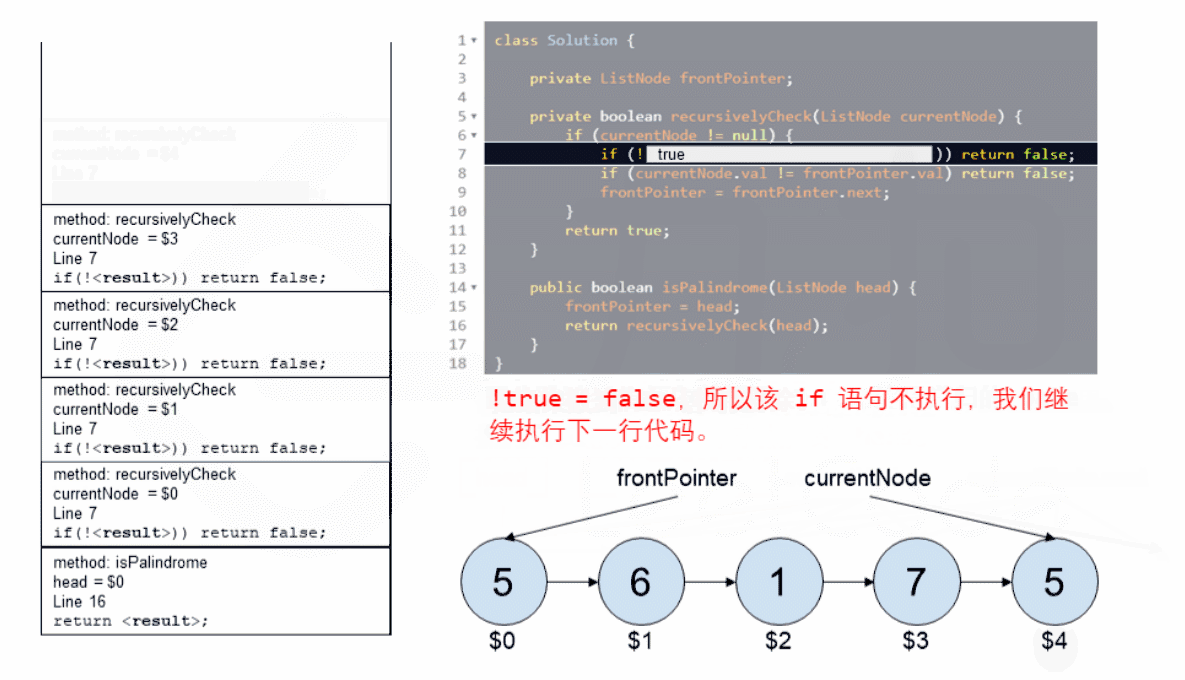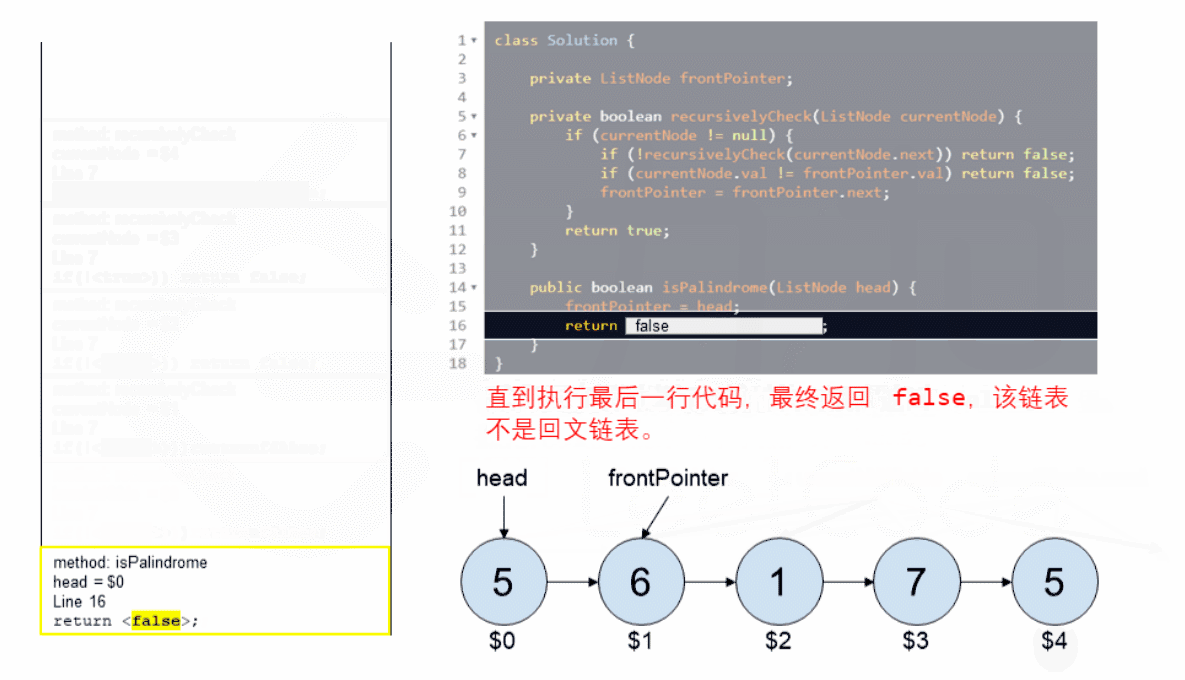
时间复杂度：O(n)，其中 n 指的是链表的大小。
空间复杂度：O(n)，其中 n 指的是链表的大小。
- 我们要理解计算机如何运行递归函数，在一个函数中调用一个函数时，计算机需要在进入被调用函数之前跟踪它在当前函数中的位置（以及任何局部变量的值），通过运行时存放在堆栈中来实现（堆栈帧）。
- 在堆栈中存放好了数据后就可以进入被调用的函数。在完成被调用函数之后，他会弹出堆栈顶部元素，以恢复在进行函数调用之前所在的函数。在进行回文检查之前，递归函数将在堆栈中创建 n 个堆栈帧，计算机会逐个弹出进行处理。所以在使用递归时空间复杂度要考虑堆栈的使用情况。
代码
let frontPointer; const recursivelyCheck = (currentNode) => { if (currentNode !== null) { if (!recursivelyCheck(currentNode.next)) { return false; } if (currentNode.val !== frontPointer.val) { return false; } frontPointer = frontPointer.next; } return true; } var isPalindrome = function(head) { frontPointer = head; return recursivelyCheck(head); };
解法三： 快慢指针
思想：
- 将链表的后半部分反转（修改链表结构）
- 然后将前半部分和后半部分进行比较。
- 比较完成后我们应该将链表恢复原样。
步骤：
- 1.找到前半部分链表的尾节点。
- 计算链表节点的数量，然后遍历链表找到前半部分的尾节点；
- 使用快慢指针在一次遍历中找到：
- 慢指针一次走一步，快指针一次走两步，快慢指针同时出发。
- 当快指针移动到链表的末尾时，慢指针恰好到链表的中间。
- 通过慢指针将链表分为两部分。
- 2.反转后半部分链表。
- 3.判断是否回文。
- 比较两个部分的值，当后半部分到达末尾则比较完成，可以忽略计数情况中的中间节点
- 4.恢复链表。
- 步骤2使用的函数相同，再反转一次恢复链表本身
- 5.返回结果。
- 1.找到前半部分链表的尾节点。
时间复杂度：O(n)，其中 n 指的是链表的大小。
空间复杂度：O(1)。我们只会修改原本链表中节点的指向，而在堆栈上的堆栈帧不超过 O(1)。
代码：
// 反转链表 const reverseList = (head) => { let prev = null; let curr = head; while (curr !== null) { let nextTemp = curr.next; curr.next = prev; prev = curr; curr = nextTemp; } return prev; } // 快慢指针法查找中间节点 const endOfFirstHalf = (head) => { let fast = head; let slow = head; while (fast.next !== null && fast.next.next !== null) { fast = fast.next.next; slow = slow.next; } return slow; } var isPalindrome = function(head) { if (head == null) return true; // 找到前半部分链表的尾节点并反转后半部分链表 const firstHalfEnd = endOfFirstHalf(head); const secondHalfStart = reverseList(firstHalfEnd.next); // 判断是否回文 let p1 = head; let p2 = secondHalfStart; let result = true; while (result && p2 != null) { if (p1.val != p2.val) result = false; p1 = p1.next; p2 = p2.next; } // 还原链表并返回结果 firstHalfEnd.next = reverseList(secondHalfStart); return result; };
合并两个有序链表
题目
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例：
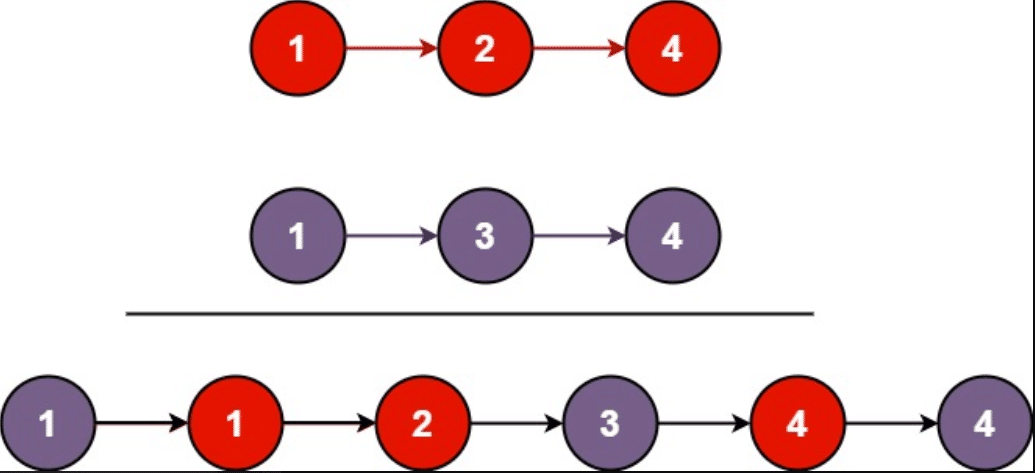
输入：l1 = [1,2,4], l2 = [1,3,4] 输出：[1,1,2,3,4,4]示例2
输入：l1 = [], l2 = [] 输出：[]示例3:
输入：l1 = [], l2 = [0] 输出：[0]提示：
- 两个链表的节点数目范围是
[0, 50] -100 <= Node.val <= 100l1和l2均按 非递减顺序 排列
- 两个链表的节点数目范围是
解法一：添加前置指针
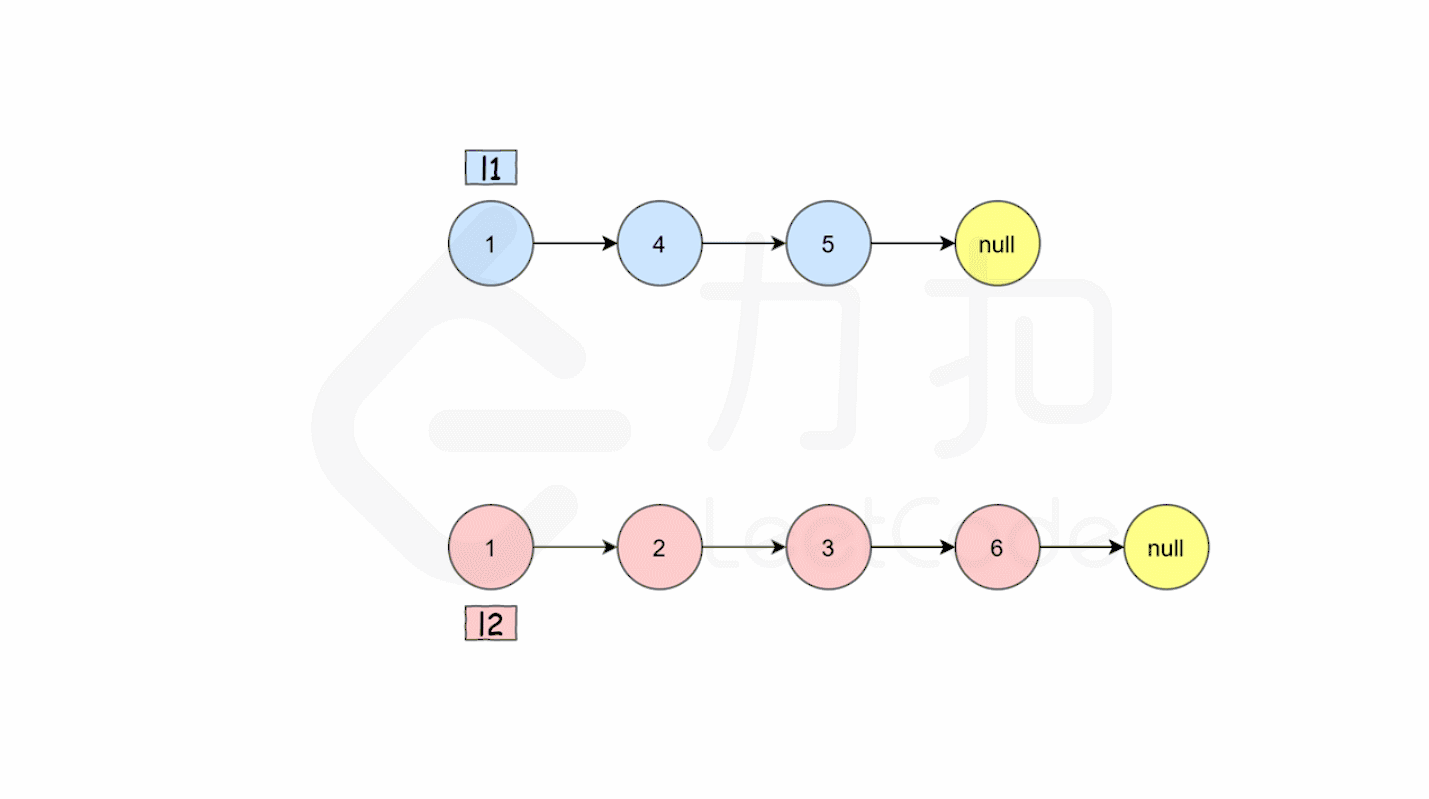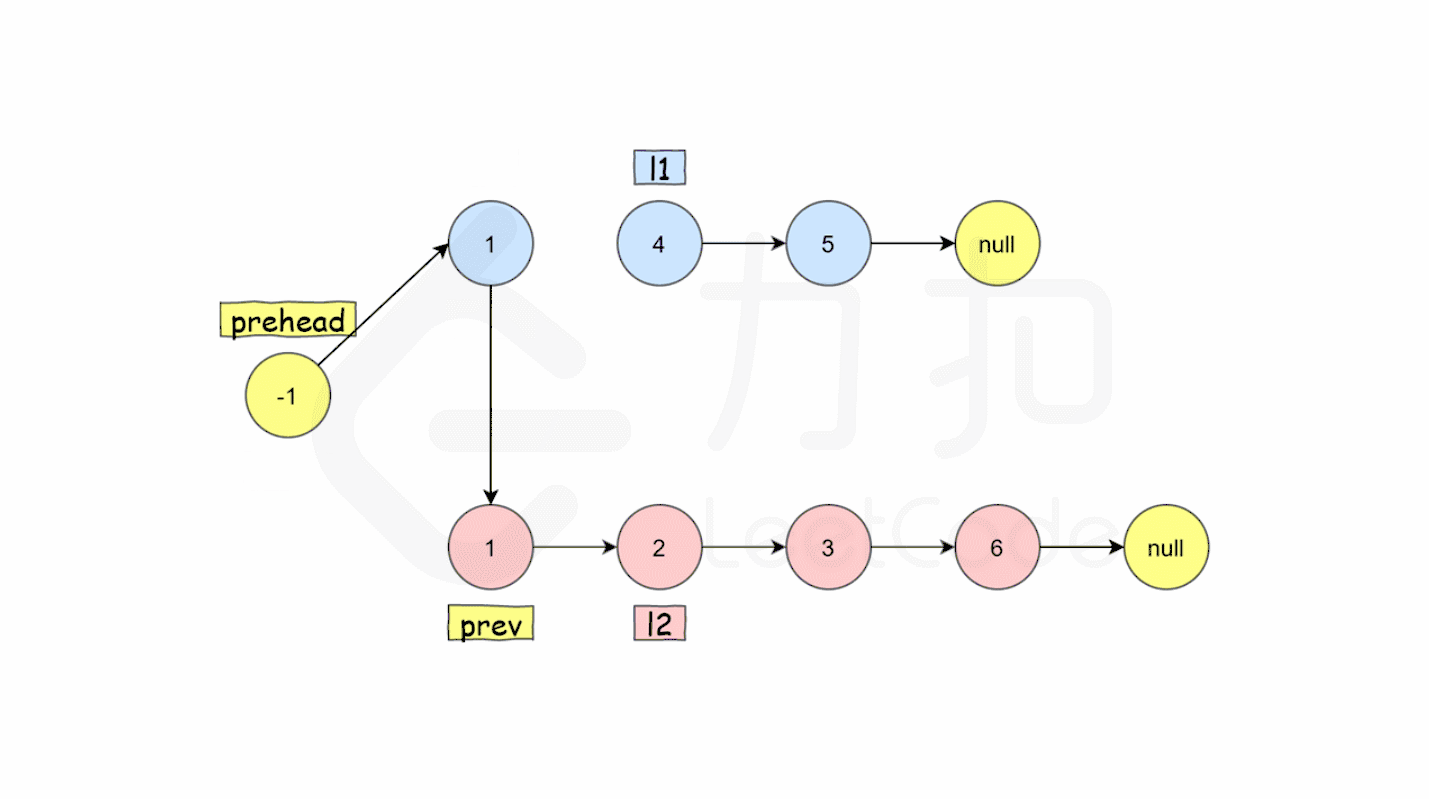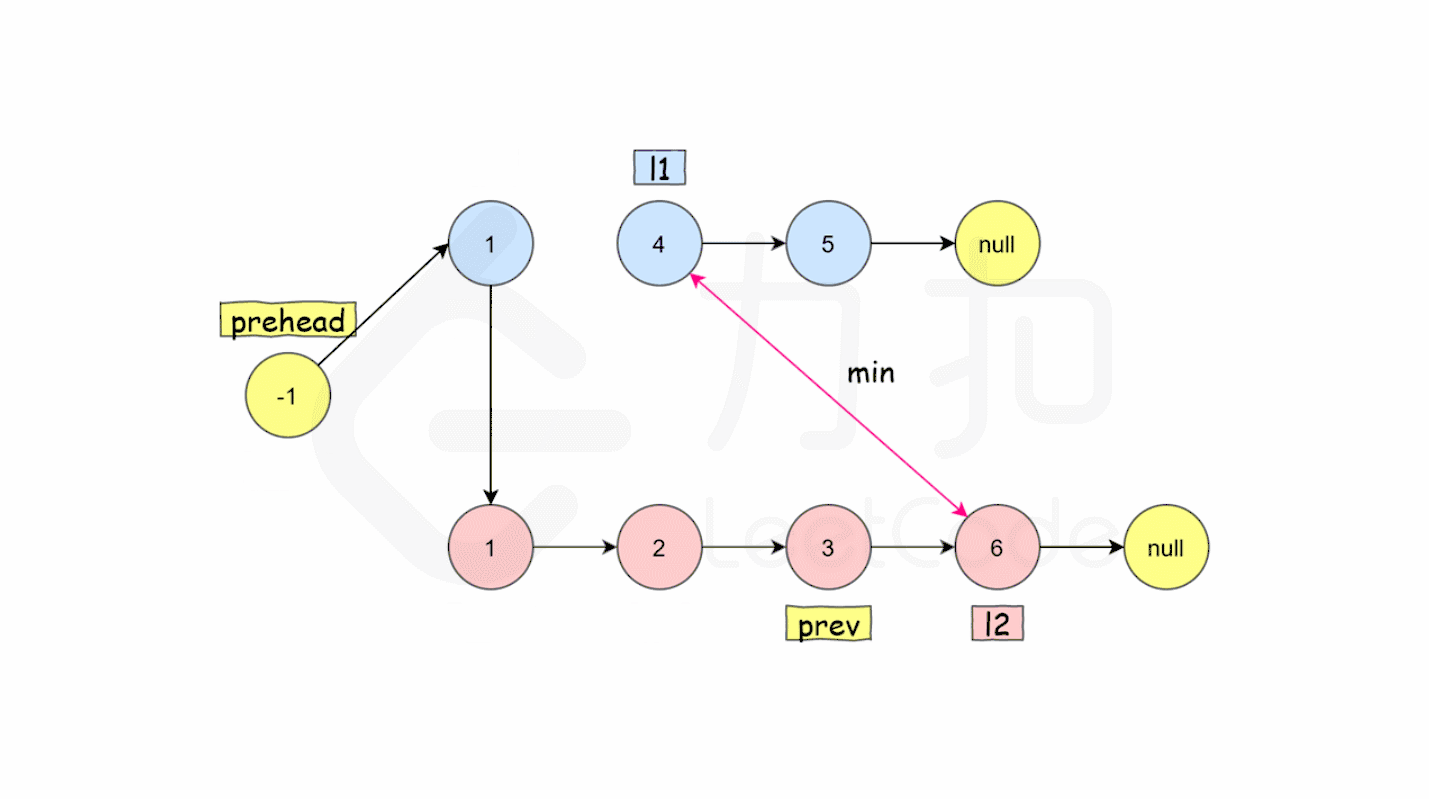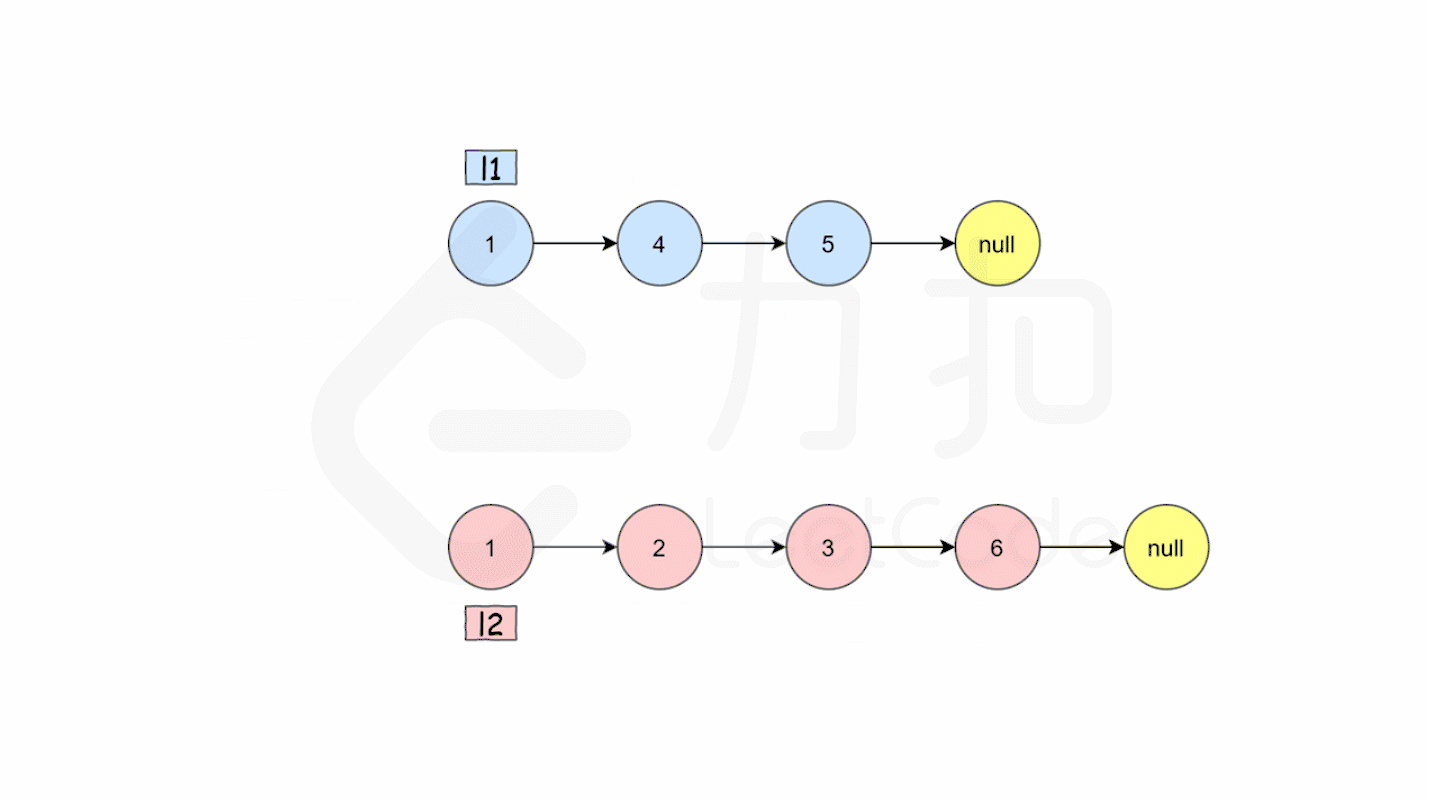
设定一个哨兵节点 prehead ，这可以在最后让我们比较容易地返回合并后的链表。
维护一个 prev 指针，调整它的 next 指针。
然后，重复以下过程，直到 l1 或者 l2 指向了 null ：
- 如果 l1 当前节点的值小于等于 l2 ，我们就把 l1 当前的节点接在 prev 节点的后面，同时将 l1 指针往后移一位。
- 否则，我们对 l2 做同样的操作。
- 然后 prev 向后移一位。
在循环终止的时候， l1 和 l2 至多有一个是非空的。由于输入的两个链表都是有序的，所以不管哪个链表是非空的，它包含的所有元素都比前面已经合并链表中的所有元素都要大（两个链表为有序链表）。因此只需要简单地将非空链表接在合并链表的后面，并返回合并链表即可。
时间复杂度：O(n+m)，其中 n 和 m 分别为两个链表的长度。因为每次循环迭代中，l1 和 l2 只有一个元素会被放进合并链表中， 因此 while 循环的次数不会超过两个链表的长度之和。所有其他操作的时间复杂度都是常数级别的，因此总的时间复杂度为 O(n+m)。
空间复杂度：O(1)。我们只需要常数的空间存放若干变量。
代码:
var mergeTwoLists = function(l1, l2) { // 创建新的前置节点 const prehead = new ListNode(-1); // 前置指针 let prev = prehead; // 循环遍历两个链表 while (l1 != null && l2 != null) { if (l1.val <= l2.val) { // 前置节点链接值较小的节点 prev.next = l1; l1 = l1.next; } else { prev.next = l2; l2 = l2.next; } prev = prev.next; // 指针后移 } // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可 prev.next = l1 === null ? l2 : l1; return prehead.next; };
解法二：递归
- 递归建模：
- 如果 l1 或者 l2 一开始就是空链表 ，那么没有任何操作需要合并，所以我们只需要返回非空链表。
- 否则，我们要判断 l1 和 l2 哪一个链表的头节点的值更小，然后递归地决定下一个添加到结果里的节点。
- 如果两个链表有一个为空，递归结束。
代码：
var mergeTwoLists = function(l1, l2) { if (l1 === null) { return l2; } else if (l2 === null) { return l1; } else if (l1.val < l2.val) { l1.next = mergeTwoLists(l1.next, l2); return l1; } else { l2.next = mergeTwoLists(l1, l2.next); return l2; } };
- 递归建模：
两数相加
- 题目:
给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。
请你将两个数相加，并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外，这两个数都不会以 0 开头。
示例：
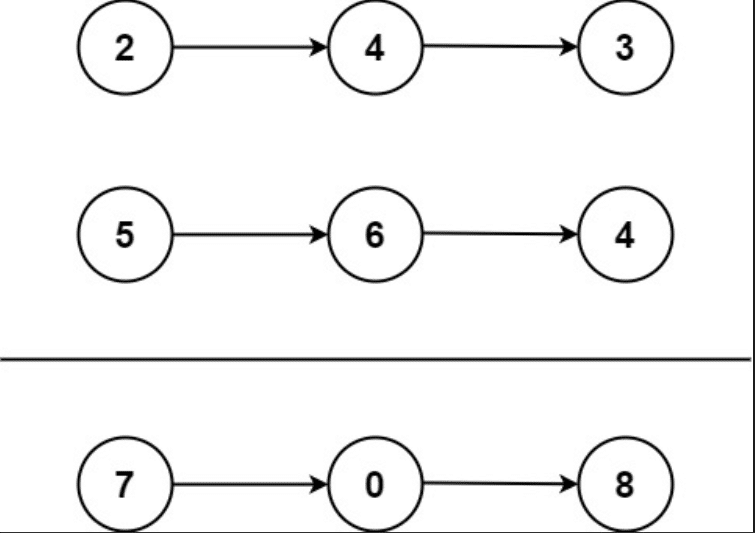
输入：l1 = [2,4,3], l2 = [5,6,4] 输出：[7,0,8] 解释：342 + 465 = 807.输入：l1 = [0], l2 = [0] 输出：[0]输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] 输出：[8,9,9,9,0,0,0,1]
提示：
- 每个链表中的节点数在范围
[1, 100]内0 <= Node.val <= 9- 题目数据保证列表表示的数字不含前导零
解法一：
- 两数字相加算法：
- 从个位数到最最高位，每一个数字进行相加；
- 相加大于10，则结果为余数，数字往上进一位，进位为整数；
- 遍历两个链表，节点一一对应相加，相加后求余数，并求进位数；
- 当两条链表都遍历结束后，如果余数不为零，则继续创建节点，将余数节点插入链表末尾；
- 代码
/** * Definition for singly-linked list. * function ListNode(val, next) { * this.val = (val===undefined ? 0 : val) * this.next = (next===undefined ? null : next) * } */ /** * @param {ListNode} l1 * @param {ListNode} l2 * @return {ListNode} */ var addTwoNumbers = function(l1, l2) { let cur1 = l1; let cur2 = l2; let head = null; let tail = null;//使用尾指针创建链表 let remain = 0; // 保存上一位整数 while(cur1 || cur2) { let val1 = cur1? cur1.val:0; let val2 = cur2? cur2.val:0; let result = val1 + val2 + remain; // 计算两数和： 两数相加并加上上一位进数 remain = Math.trunc(result/10); // 进数计算：结果除以 10 取整数 let newNode = new ListNode(result%10,null); // 结果计算：取两数之和的余数 if(!head) { head = tail = newNode; }else { tail.next = newNode; tail = newNode; } cur1 = cur1? cur1.next : null; cur2 = cur2? cur2.next : null; } if(remain !=0) { // 注意： 如果余数不为零，说明最后有进位，将进位创建节点并假如链表末尾 let newNode = new ListNode(remain,null); tail.next = newNode; tail = newNode; } return head; };- 两数字相加算法：
复制带随机指针链表
题目：
输入一个复杂链表（每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针指向任意一个节点），返回结果为复制后复杂链表的head。
示例：
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]示例2：
输入：head = [[1,1],[2,1]] 输出：[[1,1],[2,1]]示例3：
输入：head = [[3,null],[3,0],[3,null]] 输出：[[3,null],[3,0],[3,null]]
解法一：使用 MAP 映射和两次遍历链表
思路：
了复制一个复杂链表，需要遍历原链表并创建新的节点。同时，还需要处理特殊指针，即原链表节点的 random 指针，使其指向新链表中对应的节点。
具体步骤如下：
- 创建一个哈希表或映射表，用于存储原链表节点和复制链表节点的对应关系。
- 第一次遍历原链表，创建新的节点，并将原链表节点和新节点的对应关系保存到哈希表中。
- 第二次遍历原链表，处理新节点的 next 和 random 指针：
- 新节点的 next 指针指向哈希表中对应的原链表节点的 next 节点的复制节点。
- 新节点的 random 指针指向哈希表中对应的原链表节点的 random 节点的复制节点。
- 返回复制链表的头节点。
代码:
class Node { constructor(value) { this.val = value; this.next = null; this.random = null; } } function copyRandomList(head) { if (!head) { return null; } const map = new Map(); // 第一次遍历，复制节点并建立映射关系 let currentNode = head; while (currentNode) { const newNode = new Node(currentNode.val); map.set(currentNode, newNode); currentNode = currentNode.next; } // 第二次遍历，处理复制节点的指针 currentNode = head; while (currentNode) { const newNode = map.get(currentNode); newNode.next = map.get(currentNode.next); newNode.random = map.get(currentNode.random); currentNode = currentNode.next; } return map.get(head); }
解法二：
思路：
拆分成三步:
复制一份链表放在前一个节点后面，即根据原始链表的每个节点N创建N
,把N直接放在N的next位置，让复制后的链表和原始链表组成新的链表。给复制的链表random赋值，即
N.random=N.random.next。拆分链表，将N`和N进行拆分，保证原始链表不受影响。
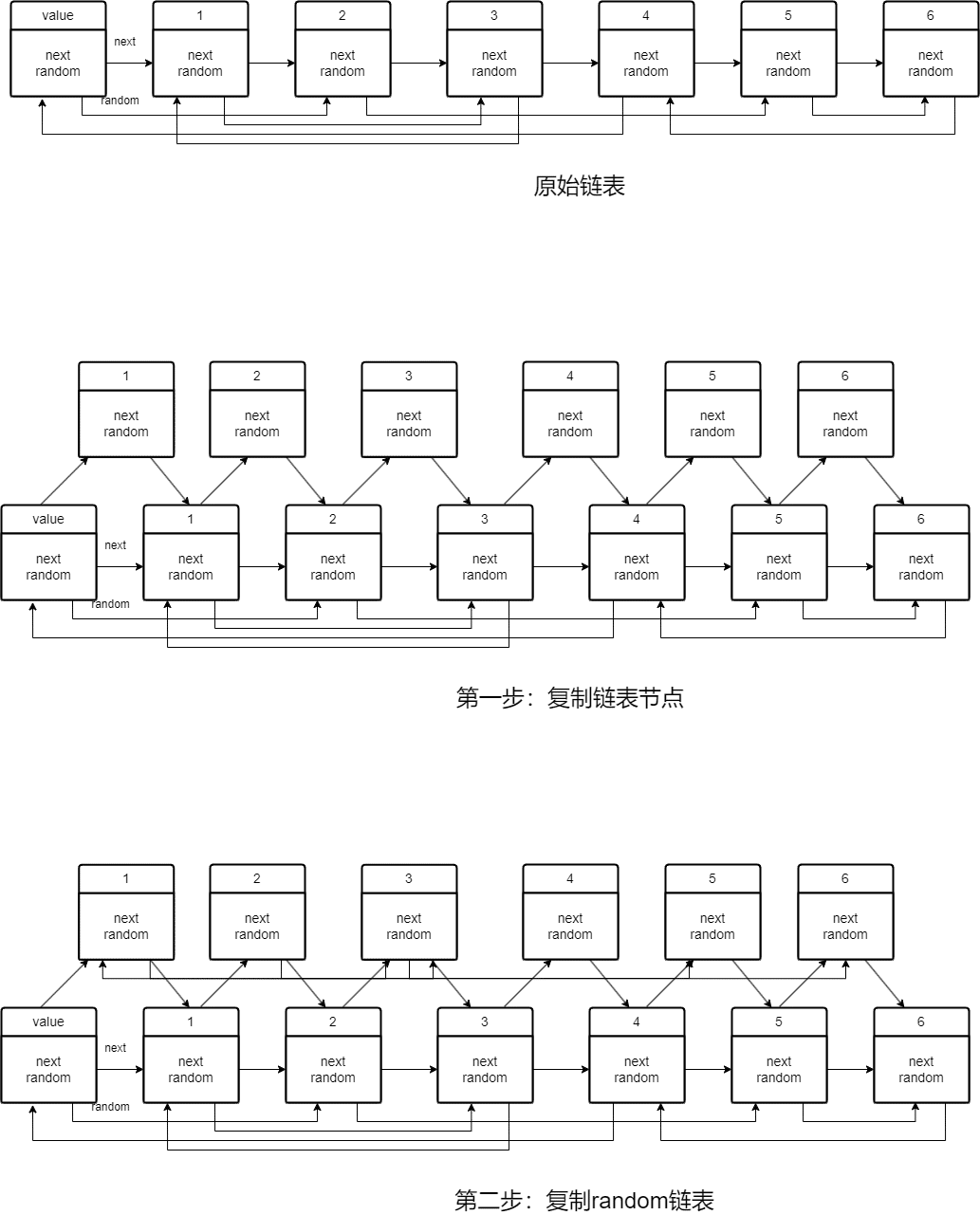
代码：
// 复制复杂链表 function Clone(pHead) { if (pHead === null) { return null; } // 第一步：复制链表节点 cloneNodes(pHead); // 第二步：复制 random 链表 cloneRandom(pHead); // 第三步： 拆分链表 return reconnetNodes(pHead); } function cloneNodes(pHead) { var current = pHead; while (current) { // 创建新节点 let cloneNode = { label: current.label, next: current.next }; // 新节点链接到当前节点前面 current.next = cloneNode; current = cloneNode.next; } } function cloneRandom(pHead) { var current = pHead; while (current) { var cloneNode = current.next; if (current.random) { cloneNode.random = current.random.next; } else { cloneNode.random = null; } current = cloneNode.next; } } function reconnetNodes(pHead) { var cloneHead = pHead.next; var cloneNode = pHead.next; var current = pHead; while (current) { current.next = cloneNode.next; current = cloneNode.next; if (current) { cloneNode.next = current.next; cloneNode = current.next; } else { cloneNode.next = null; } } return cloneHead; }
双向链表
概念
双向”指的是各节点之间的逻辑关系是双向的，头指针通常只设置一个。
结构：
指针域
prior：用于指向当前节点的直接前驱节点；数据域
value：用于存储数据元素。指针域
next：用于指向当前节点的直接后继节点。//双向链表节点结构 class Node { constructor(value) { this.prior = null; this.value = value; this.next = null; } }
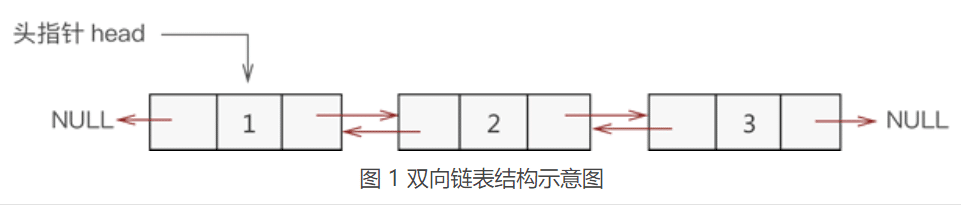
- 双向链表的特点：
- 双向遍历：由于每个节点包含了对前一个节点的引用，可以从头到尾或从尾到头进行遍历，提供了链表的双向遍历能力。
- 插入和删除操作效率高：相比单向链表，在双向链表中插入和删除节点的操作更高效。因为可以直接通过前一个节点的引用找到后一个节点，无需遍历整个链表。
- 占用更多的内存空间：由于每个节点需要存储对前一个节点的引用，相比单向链表，双向链表占用更多的内存空间。
- 实现复杂度略高：相比单向链表，双向链表的实现稍微复杂一些，需要同时维护前后两个方向的引用关系。
创建双向链表
题目：输入一个数组，根据输入数据创建双向链表
思路：
同单链表相比，双链表仅是各节点多了一个用于指向直接前驱的指针域。因此，我们可以在单链表的基础轻松实现对双链表的创建。
需要注意的是，与单链表不同，双链表创建过程中，每创建一个新节点都要与其前驱节点建立两次联系，分别是：
- 将新节点的 prior 指针指向直接前驱节点；
- 将直接前驱节点的 next 指针指向新节点；
代码：
class Node { constructor(value) { this.value = value; this.prev = null; this.next = null; } } function createDoublyLinkedList(arr) { if (!Array.isArray(arr) || arr.length === 0) { return null; // 输入数组无效 } // 头节点 const head = new Node(arr[0]); let currentNode = head; // 移动指针 for (let i = 1; i < arr.length; i++) { const newNode = new Node(arr[i]); //创建新节点 currentNode.next = newNode; // 当前节点指向新节点 newNode.prev = currentNode; // 新节点前驱指针指向当前节点 currentNode = newNode; // 指针后移 } return head; } // 示例用法 const arr = [1, 2, 3, 4, 5]; const head = createDoublyLinkedList(arr); // 打印链表元素 let currentNode = head; let result = ''; while (currentNode) { result += currentNode.value + ' '; currentNode = currentNode.next; } console.log(result.trim()); // 输出: 1 2 3 4 5
双向链表添加节点
根据数据添加到双向链表中的位置不同，可细分为以下 3 种情况：
- 添加至表头
将新数据元素添加到表头，只需要将该元素与表头元素建立双层逻辑关系即可。
换句话说，假设新元素节点为 temp，表头节点为 head，则需要做以下 2 步操作即可：
- temp->next=head; head->prior=temp;
- 将 head 移至 temp，重新指向新的表头；
例如，将新元素 7 添加至双链表的表头，则实现过程如图 2 所示：
添加至表的中间位置
同单链表添加数据类似，双向链表中间位置添加数据需要经过以下 2 个步骤，如图 3 所示：
- 新节点先与其直接后继节点建立双层逻辑关系；
- 新节点的直接前驱节点与之建立双层逻辑关系；
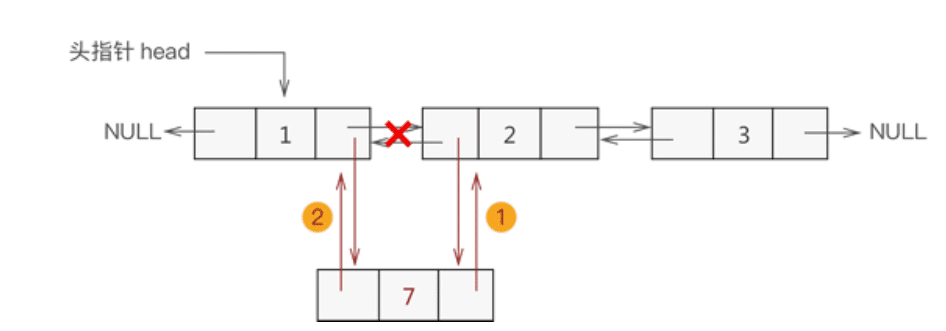
添加至表尾
与添加到表头是一个道理，实现过程如下（如图 4 所示）：
- 找到双链表中最后一个节点；
- 让新节点与最后一个节点进行双层逻辑关系；
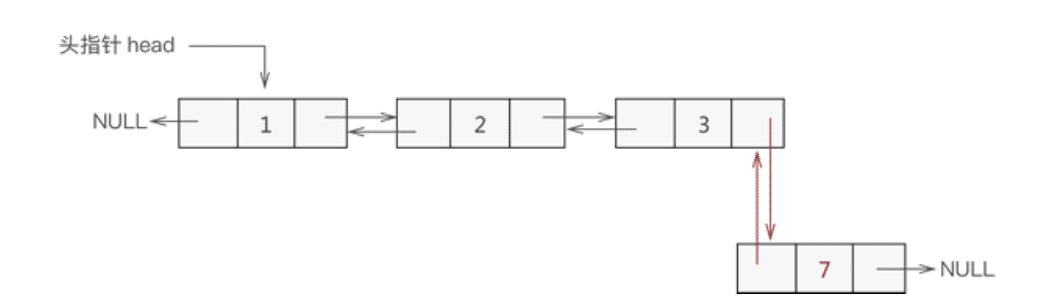
代码：
class Node { constructor(value) { this.value = value; this.prev = null; this.next = null; } } class DoublyLinkedList { constructor() { this.head = null; } // 在链表头部添加节点 prepend(value) { const newNode = new Node(value); if (!this.head) { // 如果链表为空，则新节点为头节点 this.head = newNode; } else { // 将新节点插入到头部 newNode.next = this.head; this.head.prev = newNode; this.head = newNode; } } // 在链表末尾添加节点 append(value) { const newNode = new Node(value); if (!this.head) { // 如果链表为空，则新节点为头节点 this.head = newNode; } else { // 遍历链表找到最后一个节点 let currentNode = this.head; while (currentNode.next) { currentNode = currentNode.next; } // 在最后一个节点后面添加新节点 newNode.prev = currentNode; currentNode.next = newNode; } } // 在指定位置插入节点 insertAt(value, position) { if (position < 0 || position > this.getLength()) { return false; // 位置无效 } const newNode = new Node(value); if (position === 0) { // 在头部插入节点 newNode.next = this.head; if (this.head) { this.head.prev = newNode; } this.head = newNode; } else { let currentNode = this.head; let index = 0; // 找到指定位置的前一个节点 while (index < position - 1) { currentNode = currentNode.next; index++; } // 在指定位置插入节点 newNode.prev = currentNode; // 新节点与前一个节点建立联系 newNode.next = currentNode.next;// 新节点与后一个节点建立联系 if (currentNode.next) { currentNode.next.prev = newNode; // 后一个节点与新节点建立联系 } currentNode.next = newNode; // 移动 currentNode 指针 } return true; } // 获取链表长度 getLength() { let length = 0; let currentNode = this.head; while (currentNode) { length++; currentNode = currentNode.next; } return length; } // 打印链表元素 print() { let currentNode = this.head; let result = ''; while (currentNode) { result += currentNode.value + ' '; currentNode = currentNode.next; } console.log(result.trim()); } } // 示例用法 const linkedList = new DoublyLinkedList(); linkedList.append(1); linkedList.append(2); linkedList.append(3); linkedList.print(); // 输出: 1 2 3 linkedList.prepend(0); linkedList.print(); // 输出: 0 1 2 3 linkedList.insertAt(4, 3); linkedList.print(); // 输出: 0 1 2 4 3
双向链表删除节点
和添加结点的思想类似，在双向链表中删除目标结点也分为 3 种情况。
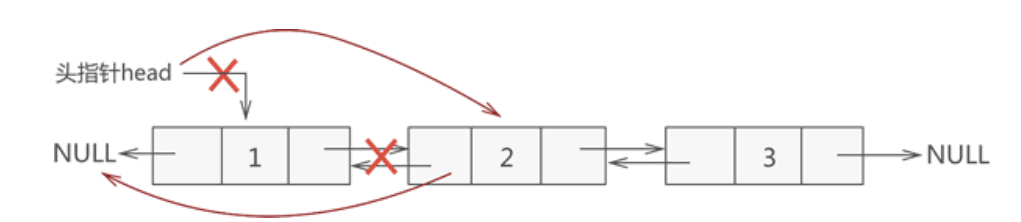
- 删除表头结点
删除表头结点的过程如下图所示：
删除表头结点的实现过程是：
- 新建一个指针指向表头结点；
- 断开表头结点和其直接后续结点之间的关联，更改 head 头指针的指向，同时将其直接后续结点的 prior 指针指向 NULL；
- 释放表头结点占用的内存空间。
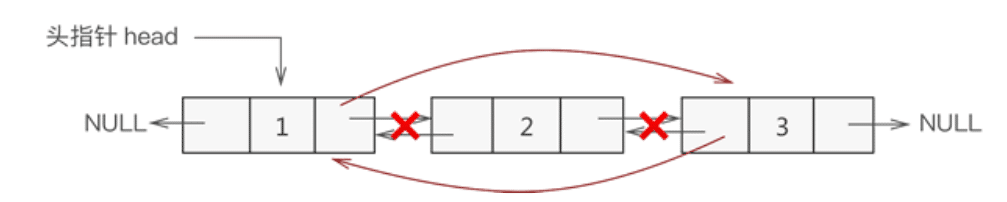
- 删除表中结点
删除表中结点的过程如下图所示：
删除表中结点的实现过程是：
- 找到目标结点，新建一个指针指向改结点；
- 将目标结点从链表上摘除；
- 释放该结点占用的内存空间。
- 删除表尾结点
删除表尾结点的过程如下图所示：
删除表尾结点的实现过程是：
- 找到表尾结点，新建一个指针指向该结点；
- 断点表尾结点和其直接前驱结点的关联，并将其直接前驱结点的 next 指针指向 NULL；
- 释放表尾结点占用的内存空间。
代码:
class Node { constructor(value) { this.value = value; this.prev = null; this.next = null; } } class DoublyLinkedList { constructor() { this.head = null; } // 删除指定值的节点 delete(value) { if (!this.head) { return; // 链表为空，无法删除 } let currentNode = this.head; // 遍历链表找到要删除的节点 while (currentNode) { if (currentNode.value === value) { if (currentNode === this.head) {// 删除头节点 // 移动 head 指针 this.head = currentNode.next; if (this.head) { this.head.prev = null; currentNode.next = null; return this.head; } } // 删除表中结点:节点前后指针都不为空，表示表中节点 if(currentNode.next && currentNode.prev){ currentNode.next.prev = currentNode.prev; currentNode.prev.next = currentNode.next; return this.head; } // 删除尾节点: currentNode.next 为空表示尾节点 if(!currentNode.next){ currentNode.prev.next = null; currentNode.next = null; return this.head; } } currentNode = currentNode.next; } } // 获取链表长度 getLength() { let length = 0; let currentNode = this.head; while (currentNode) { length++; currentNode = currentNode.next; } return length; } // 打印链表元素 print() { let currentNode = this.head; let result = ''; while (currentNode) { result += currentNode.value + ' '; currentNode = currentNode.next; } console.log(result.trim()); } } // 示例用法 const linkedList = new DoublyLinkedList(); linkedList.append(1); linkedList.append(2); linkedList.append(3); linkedList.print(); // 输出: 1 2 3 linkedList.delete(2); linkedList.print(); // 输出: 1 3 linkedList.delete(1); linkedList.print(); // 输出: 3 linkedList.delete(3); linkedList.print(); // 输出:
扁平化多级双向链表
题目：
多级双链表是一个双链表，其中包含的节点有一个下一个指针、一个前一个指针和一个额外的 子指针 。
- 这个子指针可能指向一个单独的双向链表，也包含这些特殊的节点。
- 这些子列表可以有一个或多个自己的子列表，以此类推，以生成如下面的示例所示的 多层数据结构 。
给定链表的头节点 head ，将链表 扁平化 ，以便所有节点都出现在单层双链表中。
让 curr 是一个带有子列表的节点。子列表中的节点应该出现在扁平化列表中的 curr 之后 和 curr.next 之前 。
返回 扁平列表的 head 。列表中的节点必须将其 所有 子指针设置为 null 。
示例 1：
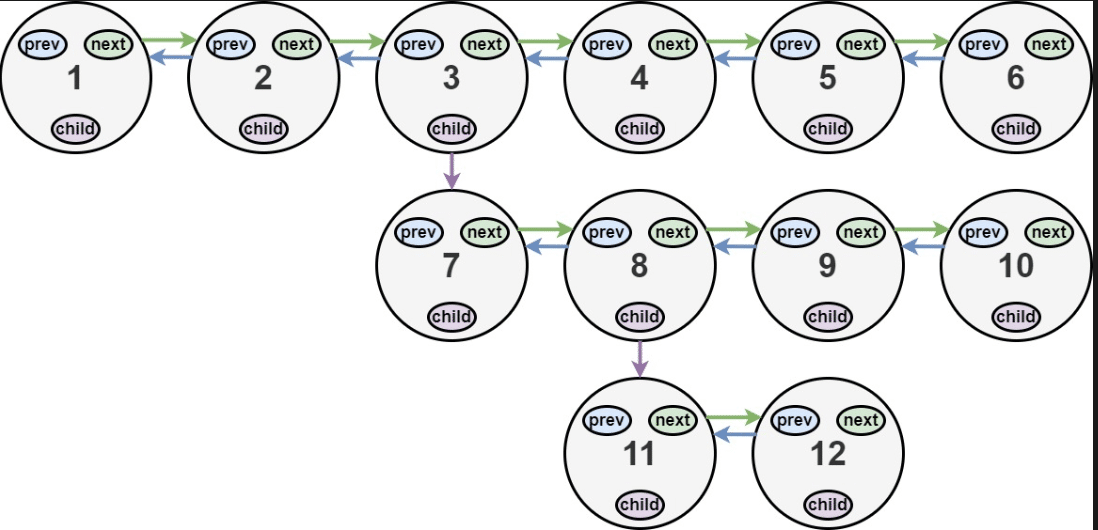
输入：head = [1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12] 输出：[1,2,3,7,8,11,12,9,10,4,5,6] 解释：输入的多级列表如上图所示。扁平化后的链表如下图：
示例 2：
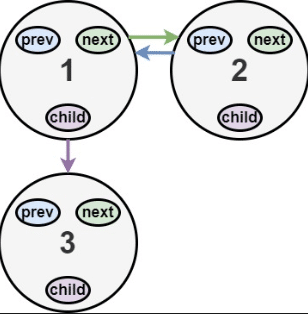
输入：head = [1,2,null,3] 输出：[1,3,2] 解释：输入的多级列表如上图所示。扁平化后的链表如下图：
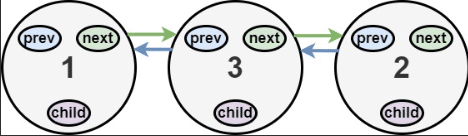
示例 3：
输入：head = [] 输出：[] 说明：输入中可能存在空列表。
提示：
节点数目不超过 1000 1 <= Node.val <= 105
如何表示测试用例中的多级链表？
以 示例 1 为例：
1---2---3---4---5---6--NULL | 7---8---9---10--NULL | 11--12--NULL序列化其中的每一级之后：
[1,2,3,4,5,6,null] [7,8,9,10,null] [11,12,null]为了将每一级都序列化到一起，我们需要每一级中添加值为 null 的元素，以表示没有节点连接到上一级的上级节点。
[1,2,3,4,5,6,null] [null,null,7,8,9,10,null] [null,11,12,null]合并所有序列化结果，并去除末尾的 null 。
[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12]
解法：深度优先搜索
当我们遍历到某个节点 node 时，如果它的 child 成员不为空，那么我们需要将 child 指向的链表结构进行扁平化，并且插入 node 与 node 的下一个节点之间;
在遇到 child 成员不为空的节点时，就要先去处理 child 指向的链表结构:
对 child 指向的链表结构的扁平化之后，就可以「回溯」到 node 节点;
为了能够将扁平化的链表插入 node 与 node 的下一个节点之间，我们需要知道扁平化的链表的最后一个节点 last，随后进行如下的三步操作：
将 node 与 node 的下一个节点 next 断开：
将 node 与 child 相连；
将 last 与 next 相连。
在深度优先搜索完成后，我们返回给定的首节点即可。
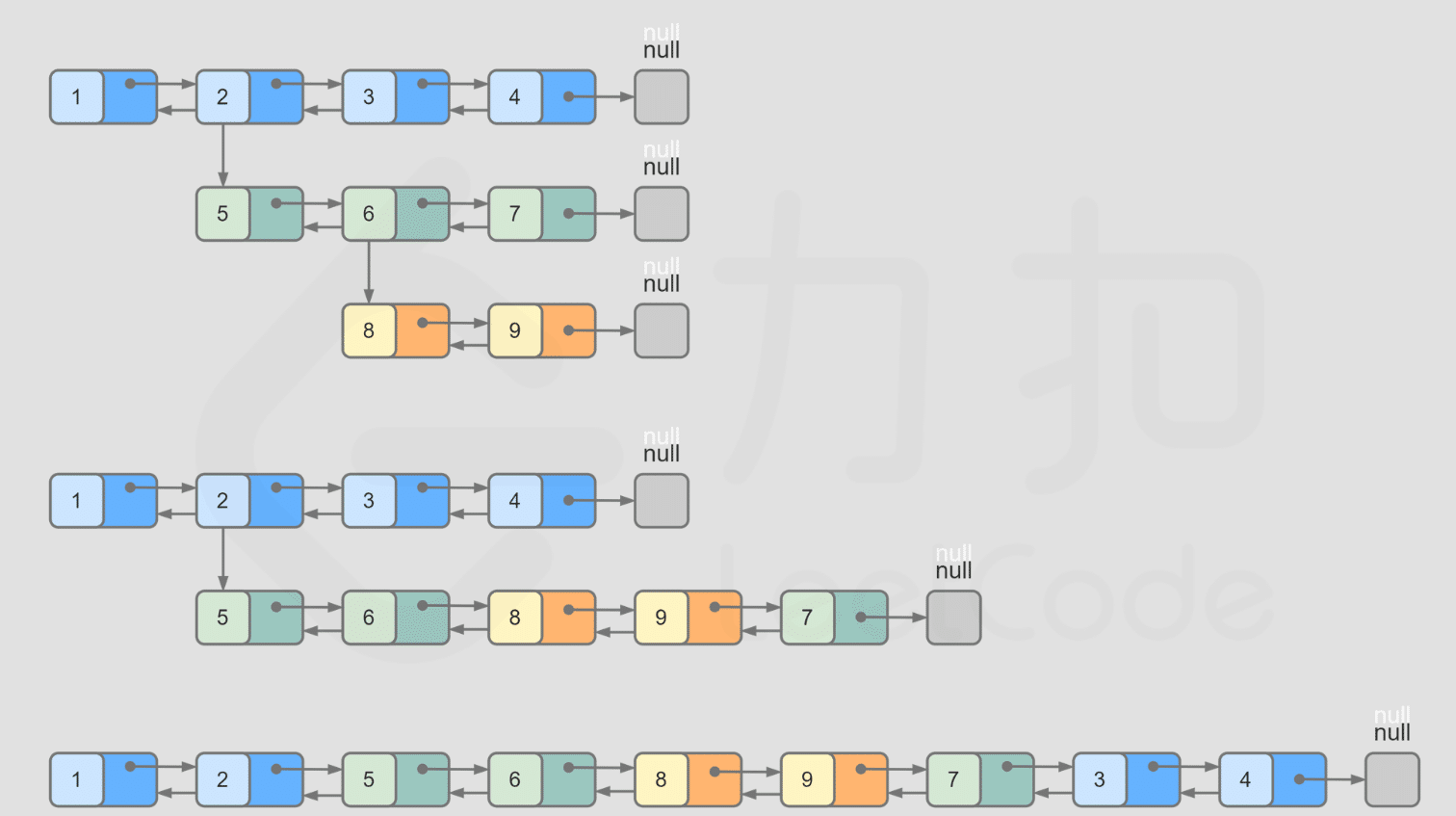
复杂度分析
- 时间复杂度：O(n)，其中n 是链表中的节点个数。
- 空间复杂度：O(n)。上述代码中使用的空间为深度优先搜索中的栈空间，如果给定的链表的「深度」为 d，那么空间复杂度为 O(d)。在最换情况下，链表中的每个节点的 next 都为空，且除了最后一个节点外，每个节点的 child 都不为空，整个链表的深度为 n，因此时间复杂度为 O(n)。
代码: 深度优先搜索的递归写法
var flatten = function(head) { // 深度优先搜索 const dfs = (node) => { let cur = node; // 记录链表的最后一个节点 let last = null; while (cur) { let next = cur.next; // 如果有子节点，那么首先处理子节点 if (cur.child) { // 深度搜索子节点，获取子节点的最后一个节点 childLast const childLast = dfs(cur.child); // next = cur.next; // 将 node 与 child 相连 cur.next = cur.child; cur.child.prev = cur; // 如果 next 不为空，就将 last 与 next 相连 if (next != null) { childLast.next = next; next.prev = childLast; } // 将 child 置为空 cur.child = null; last = childLast; } else { // 没有子节点，将 last 指针指向移动的 cur 指针 last = cur; } // cur 指针后移 cur = next; } // 移动到最后一个节点后，返回最后一个节点指针 return last; } dfs(head); return head; };代码： 深度优先搜索的栈写法
var flatten = function(head) { if (!head) return null; const stack = []; // 栈用于保存含有 child 节点的 next 节点 let cur = head; let prev = null; while (cur || stack.length > 0) { // 指针移遍历到末尾，则直接出栈 if (!cur) { cur = stack.pop(); } // 遍历的节点存在子节点，则对子节点进行遍历 if (cur.child) { if (cur.next) {//注意：当前节点存在 next 节点才需要入栈等待回溯，没有 next 不需要回溯，则无需入栈 stack.push(cur.next); } // 直接将含有 child 的节点 与它的child 节点链接 cur.next = cur.child; cur.child.prev = cur; cur.child = null; } prev = cur; cur = cur.next; // 指针后移 // 遍历到最后一个节点时，获取栈顶元素，将左右一个节点与栈顶元素节点链接 if (!cur && stack.length > 0) { prev.next = stack[stack.length - 1]; stack[stack.length - 1].prev = prev; } } return head; };
循环链表
概念
循环链表是一种特殊类型的链表，其中链表中的最后一个节点指向第一个节点，形成一个闭环的结构。
循环链表没有尾节点，而是通过尾节点的指针将链表的末尾连接到头节点。
分类：
- 单向循环链表：在单向循环链表中，每个节点只有一个指针，指向下一个节点，而最后一个节点指向头节点。这种循环链表可以实现环形队列等应用。
- 双向循环链表：在双向循环链表中，每个节点有两个指针，一个指向前一个节点，另一个指向后一个节点。最后一个节点的后继节点是头节点，头节点的前驱节点是最后一个节点。这种循环链表可以支持双向遍历和操作，例如在双向循环链表中可以方便地进行插入和删除操作。
优势：
- 遍历方便：由于循环链表形成了闭环结构，可以从任意节点开始遍历整个链表，不需要额外的终止条件。这使得循环链表在某些情况下更加方便和高效。
- 插入和删除操作高效：在循环链表中，插入和删除节点的操作相对于非循环链表更加高效。由于节点的前驱和后继节点都可以直接访问，插入和删除操作不需要遍历整个链表来定位位置，因此时间复杂度较低。
- 实现循环结构：循环链表的最后一个节点指向头节点，形成了一个循环结构。这种结构在某些问题和算法中非常有用，例如模拟循环队列、循环缓冲区等应用场景。
单向循环链表
创建单向循环链表
题目：输入一组数据，根据输入数据创建单向循环链表
思路：
创建循环链表方法跟创建链表方法相同，但是循环链表判断一次遍历结束方式不同： currentNode.next !== this.head
代码：
class Node { constructor(value) { this.value = value; this.next = null; } } class CircularLinkedList { constructor() { this.head = null; } // 添加节点到链表尾部 append(value) { const newNode = new Node(value); if (!this.head) { // 如果链表为空，则新节点为头节点 this.head = newNode; newNode.next = this.head; // 将头节点指向自己形成循环 } else { let currentNode = this.head; // 找到最后一个节点，注意判断条件 while (currentNode.next !== this.head) { currentNode = currentNode.next; } // 在最后一个节点后面添加新节点 currentNode.next = newNode; newNode.next = this.head; // 将新节点的 next 指向头节点，形成循环 } } // 打印循环链表 print() { if (!this.head) { console.log("循环链表为空"); return; } let currentNode = this.head; let nodes = []; // 遍历循环链表，将节点值存入数组 do { nodes.push(currentNode.value); currentNode = currentNode.next; } while (currentNode !== this.head); console.log(nodes.join(" -> ")); } } // 示例用法 const input = [1, 2, 3, 4, 5]; const circularLinkedList = new CircularLinkedList(); for (let i = 0; i < input.length; i++) { circularLinkedList.append(input[i]); } circularLinkedList.print(); // 输出: 1 -> 2 -> 3 -> 4 -> 5 -> 1
双向循环链表
- 双向循环链表是一种特殊类型的链表，每个节点都有一个指向前一个节点和一个指向后一个节点的指针。
- 与单向循环链表不同，双向循环链表可以在两个方向上遍历和操作链表。
- 双向循环链表的特点和优势包括：
- 双向遍历：双向循环链表可以从头节点或尾节点开始，沿着前向或后向指针遍历整个链表。这使得在某些情况下可以更方便和高效地进行双向遍历操作。
- 插入和删除操作高效：由于每个节点都有指向前后节点的指针，插入和删除节点的操作比单向链表更高效。可以直接访问前后节点，无需遍历链表来定位位置，从而降低了时间复杂度。
创建双向循环链表
题目：输入一组数据，根据输入数据创建双向循环链表（该双向循环链表没有尾指针）
思路：
- 创建新的节点
- 根据头指针的 head.prev 找到尾部节点
- 将新的节点插入头节点和尾节点之间
代码：
class Node { constructor(value) { this.value = value; this.prev = null; this.next = null; } } class DoublyCircularLinkedList { constructor() { this.head = null; } // 添加节点到链表尾部 append(value) { const newNode = new Node(value); if (!this.head) { // 如果链表为空，则新节点为头节点 this.head = newNode; newNode.prev = newNode; newNode.next = newNode; } else { const tailNode = this.head.prev; // 通过头指针找到当前尾节点 newNode.prev = tailNode; // 链接新节点和尾节点 newNode.next = this.head; // 链接新节点和头节点 tailNode.next = newNode;// 链接新节点和尾节点 this.head.prev = newNode;// 链接新节点和头节点 } } // 打印双向循环链表 print() { if (!this.head) { console.log("双向循环链表为空"); return; } let currentNode = this.head; let nodes = []; // 遍历双向循环链表，将节点值存入数组 do { nodes.push(currentNode.value); currentNode = currentNode.next; } while (currentNode !== this.head); console.log(nodes.join(" <-> ")); } } // 示例用法 const input = [1, 2, 3, 4, 5]; const doublyCircularLinkedList = new DoublyCircularLinkedList(); for (let i = 0; i < input.length; i++) { doublyCircularLinkedList.append(input[i]); } doublyCircularLinkedList.print(); // 输出: 1 <-> 2 <-> 3 <-> 4 <-> 5
约瑟夫环问题
题目：
- 约瑟夫环问题，是一个经典的循环链表问题
- 题意是：已知 n 个人（分别用编号 1，2，3，…，n 表示）围坐在一张圆桌周围，从编号为 k 的人开始顺时针报数，数到 m 的那个人出列；他的下一个人又从 1 开始，还是顺时针开始报数，数到 m 的那个人又出列；依次重复下去，直到圆桌上剩余一个人。
- 如图 2 所示，假设此时圆周周围有 5 个人，要求从编号为 3 的人开始顺时针数数，数到 2 的那个人出列：
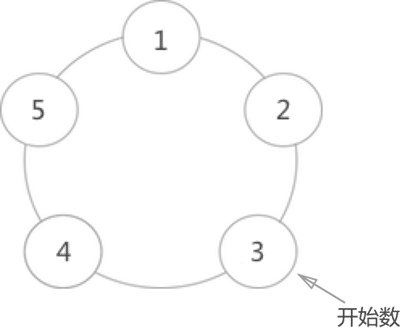图 2 循环链表实现约瑟夫环 出列顺序依次为： - 编号为 3 的人 开始数 1，4 数 2，所以 4 先出列；
- 4 出列后，从 5 开始数 1，1 数 2，所以 1 出列；
- 1 出列后，从 2 开始数 1，3 数 2，所以 3 出列；
- 3 出列后，从 5 开始数 1，2 数 2，所以 2 出列；
- 最后只剩下 5 自己，所以 5 胜出。
循环链表法
思路：
根据输入的人数
n创建循环链表。我们从头节点开始，依次创建n个节点，将它们连接成循环链表，最后将最后一个节点的next指针指向头节点，形成循环。在
josephus方法中，我们解决约瑟夫问题:- 我们首先找到起始位置的节点，即从编号为
k的人开始报数。 - 然后，我们使用一个循环来模拟报数的过程，每次数到
m，就移除当前节点，并输出出列人的编号。 - 当循环链表中只剩下一个节点时，即停止循环，并输出剩余人的编号。
- 我们首先找到起始位置的节点，即从编号为
代码：
class Node { constructor(value) { this.value = value; this.next = null; } } class CircularLinkedList { constructor() { this.head = null; } // 创建循环链表 createCircularList(n) { if (n <= 0) { throw new Error("输入的人数必须大于0"); } this.head = new Node(1); let currentNode = this.head; for (let i = 2; i <= n; i++) { const newNode = new Node(i); currentNode.next = newNode; currentNode = newNode; } currentNode.next = this.head; // 将最后一个节点的 next 指针指向头节点，形成循环 } // 解决约瑟夫问题 josephus(k, m) { if (!this.head) { throw new Error("循环链表为空"); } let currentNode = this.head; // 找到起始位置的节点 for (let i = 1; i < k; i++) { currentNode = currentNode.next; } let count = 0; let prevNode = null; //前一个节点指针 // 跳出条件：当前节点 next 指向自己，表示只剩下一个节点 while (currentNode.next !== currentNode) { count++; // 循环计数器 // 数到 m，移除当前节点 if (count === m) { if (prevNode) { // 删除当前节点 prevNode.next = currentNode.next; } else { this.head = currentNode.next; } console.log("出列人编号：" + currentNode.value); count = 0; } else { //移动前一个指针 prevNode = currentNode; } // 移动指针 currentNode = currentNode.next; } console.log("剩余人编号：" + currentNode.value); } } // 示例用法 const n = 7; // 总人数 const k = 3; // 起始位置 const m = 4; // 报数到 m const circularLinkedList = new CircularLinkedList(); circularLinkedList.createCircularList(n); circularLinkedList.josephus(k, m);
旋转链表
题目：
给你一个链表的头节点
head，旋转链表，将链表每个节点向右移动k个位置.示例：
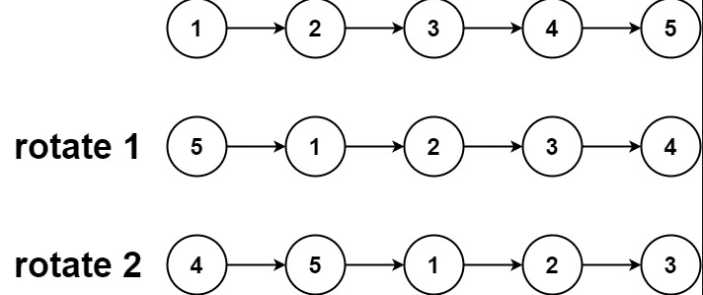
输入：head = [1,2,3,4,5], k = 2 输出：[4,5,1,2,3]
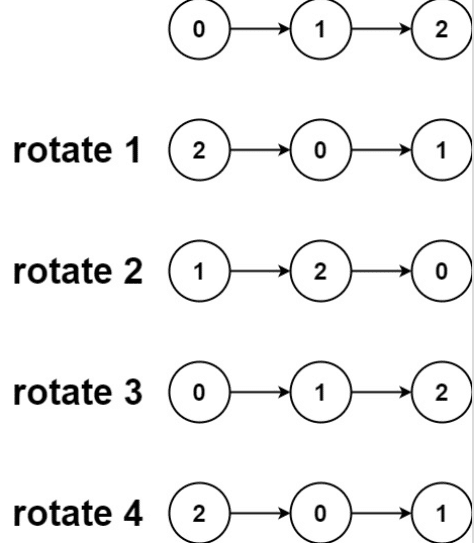
输入：head = [0,1,2], k = 4 输出：[2,0,1]
解法：闭合为环
- 将链表进行闭合形成环：计算出链表的长度 n，并找到该链表的末尾节点，将其与头节点相连；
- 当向右移动的次数 k 时，我们仅需要向右移动
k mod n次即可，即头节点旋转到原来的(n−1)−(k mod n)的位置； （因为每 n 次移动都会让链表变为原状。新链表的最后一个节点为原链表的第(n−1)−(k mod n)个节点（从 0 开始计数）) - 找到新链表的最后一个节点（即原链表的第
(n−1)−(k mod n)个节点），将当前闭合为环的链表断开，即可得到我们所需要的结果。 - 特别地，当链表长度不大于 1，或者 k 为 n的倍数时，新链表将与原链表相同，我们无需进行任何处理。
代码：
var rotateRight = function(head, k) { // 循环次数为0，或为空节点，或只有一个节点，直接返回 if (k === 0 || !head || !head.next) { return head; } let n = 1; let cur = head; while (cur.next) { //计算链表长度，并将 cur 移动到末尾节点 cur = cur.next; n++; } let add = n - k % n; // 计算旋转次数 if (add === n) { // 当 add === n 时，旋转次数刚好为链表长度的整数倍，此时相当于没有移动，直接返回 return head; } cur.next = head; // 链接首尾节点 while (add) { // 找到尾节点位置： 旋转次数等于尾节点移动到原来的 add 的位置 cur = cur.next; add--; } const ret = cur.next; // 记录头节点： 尾节点的下一个节点为头节点 cur.next = null; // 断开头尾节点链接 return ret; // 返回头节点 };
带环链表
概念
带环链表（Cyclic Linked List）是一种链表数据结构，其中链表中的一个或多个节点形成一个环，即链表的尾节点指向链表中的某个前面的节点，而不是指向空值（null）。
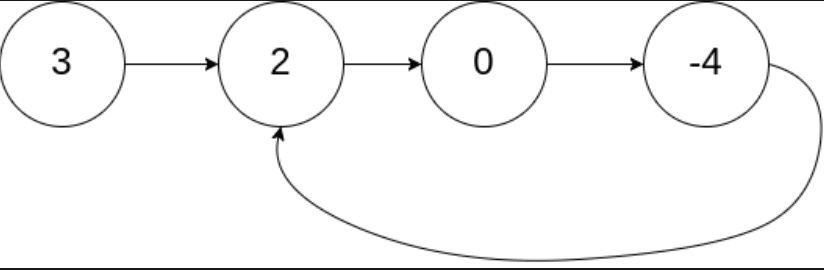
带环链表具有以下特点：
- 存在环：带环链表至少有一个环，即链表中的某个节点的指针指向链表中的前面节点，形成一个环。
- 无尽循环：由于有环存在，所以从头节点开始遍历带环链表时，永远不会到达链表的末尾，而是无限循环在环中。
带环链表和循环链表区别：
循环链表是一种特殊的链表，其中链表的尾节点指向链表的头节点，形成一个闭环。它的特点是最后一个节点的指针指向链表的头部，而不是指向空值。循环链表可以是有序的或无序的，但不一定存在环。
带环链表是一种链表，其中链表中的一个或多个节点形成一个环，即链表的尾节点指向链表中的某个前面的节点，而不是指向空值。带环链表一定存在环，且环的长度可以是任意的。
区别总结如下：
- 循环链表可能存在环，也可能没有环，而带环链表一定存在环。
- 循环链表的尾节点指向链表的头节点形成闭环，而带环链表的尾节点指向链表中的某个前面的节点，形成环。
- 循环链表的环长度是固定的，即链表中的节点个数；而带环链表的环长度可以是任意的，环的位置和长度不固定。
需要注意的是，术语的使用可能在不同的上下文中有所不同。有时候，循环链表和带环链表这两个术语也可以互换使用，但根据上述定义和常见的语义，循环链表和带环链表是有区别的
判断链表中是否有环
题目：
- 给你一个链表的头节点 head ，判断链表中是否有环。
- 如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。
- 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。
- 注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
- 如果链表中存在环 ，则返回 true 。 否则，返回 false 。
- 示例 1：
输入：head = [3,2,0,-4], pos = 1 输出：true 解释：链表中有一个环，其尾部连接到第二个节点。示例 2：
输入：head = [1,2], pos = 0 输出：true 解释：链表中有一个环，其尾部连接到第一个节点。示例 3：
输入：head = [1], pos = -1 输出：false 解释：链表中没有环。提示：
链表中节点的数目范围是 [0, 104] -105 <= Node.val <= 105 pos 为 -1 或者链表中的一个 有效索引 。
- 进阶：你能用 O(1)（即，常量）内存解决此问题吗？
哈希表法
思路
遍历所有节点，每次遍历到一个节点时，判断该节点此前是否被访问过。
使用哈希表来存储所有已经访问过的节点。
每次我们到达一个节点，如果该节点已经存在于哈希表中，则说明该链表是环形链表，否则就将该节点加入哈希表中。
重复这一过程，直到我们遍历完整个链表即可。
时间复杂度：O(N)，其中 N 是链表中的节点数。最坏情况下我们需要遍历每个节点一次。
空间复杂度：O(N)，其中 N 是链表中的节点数。主要为哈希表的开销，最坏情况下我们需要将每个节点插入到哈希表中一次。
代码：
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {boolean}
*/
let hasCycle = function(head) {
let map=new Map();//创建 Map 表
while(head){ // 不存在环时 head 为 null，存在时通过 return 终结
if(map.get(head))
return true; // 终止循环方式直接通过找到环终结
map.set(head,true); // 将整个节点作为 Map 的 key值存入 map
head=head.next;
}
return false;
};
快慢指针法
思路：
本方法需要读者对「Floyd 判圈算法」（又称龟兔赛跑算法）有所了解。
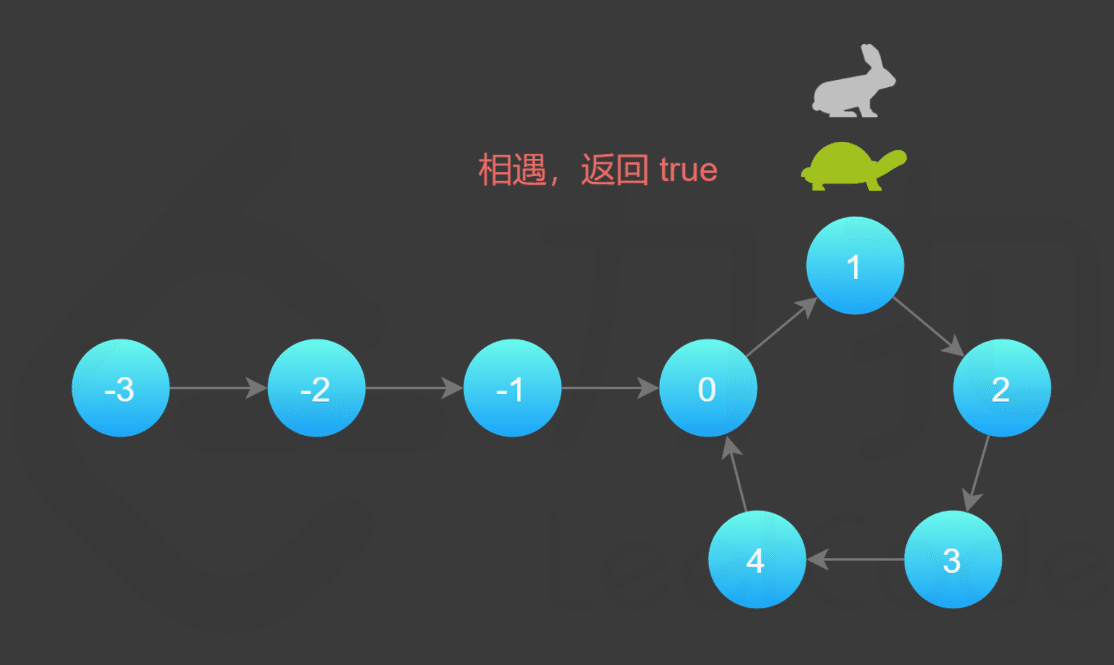
- 假想「乌龟」和「兔子」在链表上移动，「兔子」跑得快，「乌龟」跑得慢。
- 当「乌龟」和「兔子」从链表上的同一个节点开始移动时，如果该链表中没有环，那么「兔子」将一直处于「乌龟」的前方；
- 如果该链表中有环，那么「兔子」会先于「乌龟」进入环，并且一直在环内移动。
- 等到「乌龟」进入环时，由于「兔子」的速度快，它一定会在某个时刻与乌龟相遇，即套了「乌龟」若干圈。
我们可以根据上述思路来解决本题:
具体地，我们定义两个指针，一快一慢。
慢指针每次只移动一步，而快指针每次移动两步。
初始时，慢指针在位置 head，而快指针在位置 head.next。
这样一来，如果在移动的过程中，快指针反过来追上慢指针，就说明该链表为环形链表。
否则快指针将到达链表尾部，该链表不为环形链表。
为什么我们要规定初始时慢指针在位置 head，快指针在位置 head.next，而不是两个指针都在位置 head（即与「乌龟」和「兔子」中的叙述相同）？
- 观察下面的代码，我们使用的是 while 循环，循环条件先于循环体。
- 由于循环条件一定是判断快慢指针是否重合，如果我们将两个指针初始都置于 head，那么 while 循环就不会执行。
- 因此，我们可以假想一个在 head 之前的虚拟节点，慢指针从虚拟节点移动一步到达 head，快指针从虚拟节点移动两步到达 head.next，这样我们就可以使用 while 循环了。
当然，我们也可以使用 do-while 循环。此时，我们就可以把快慢指针的初始值都置为 head
代码：
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {boolean}
* 本方案采用双指针的方式，定义两指针slow，fast。
* slow 每次移动一个节点，fast每次移动两个节点，
* 如果链表存在环，则在某时刻slow与fast指针将重合，
* 如果不存在环，则能正常遍历完成链表
*/
let hasCycle = function(head) {
if(!head)return false
let slow = head,
fast = head.next
while(fast && fast.next){// 终止条件：快慢指针所指节点 next 指针都为空，表示不存在环
if(slow == fast)return true; // 快慢指针相遇，表示存在环
slow=slow.next;
fast=fast.next.next;
}
return false
};
链表环的入口节点
题目：
定一个链表的头节点 head ，返回链表开始入环的第一个节点。
如果链表无环，则返回 null。
- 如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。
- 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。
- 如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1：
输入：head = [3,2,0,-4], pos = 1 输出：返回索引为 1 的链表节点 解释：链表中有一个环，其尾部连接到第二个节点。
- 示例2：
输入：head = [1,2], pos = 0 输出：返回索引为 0 的链表节点 解释：链表中有一个环，其尾部连接到第一个节点。
- 示例3：
输入：head = [1], pos = -1 输出：返回 null 解释：链表中没有环。
提示：
- 链表中节点的数目范围在范围 [0, 104] 内
- -105 <= Node.val <= 105
- pos 的值为 -1 或者链表中的一个有效索引
进阶：你是否可以使用 O(1) 空间解决此题？
哈希表法
思路：
- 使用 hash 表存储已访问过的节点；
- 循环遍历链表：如果节点存在，直接返回该节点；
- 否则跳出循环表示没有环；
代码
var detectCycle = function(head) {
const visited = new Set();
while (head !== null) {
if (visited.has(head)) {
return head;
}
visited.add(head);
head = head.next;
}
return null;
};
复杂度分析
时间复杂度：O(N) ，其中 N 为链表中节点的数目。我们恰好需要访问链表中的每一个节点。
空间复杂度：O(N) ，其中 N 为链表中节点的数目。我们需要将链表中的每个节点都保存在哈希表当中。
快慢指针法
思路：
- 我们使用两个指针，fast与 slow。它们起始都位于链表的头部。
- 随后，slow 指针每次向后移动一个位置，而 fast 指针向后移动两个位置。
- 如果链表中存在环，则 fast 指针最终将再次与 slow 指针在环中相遇。
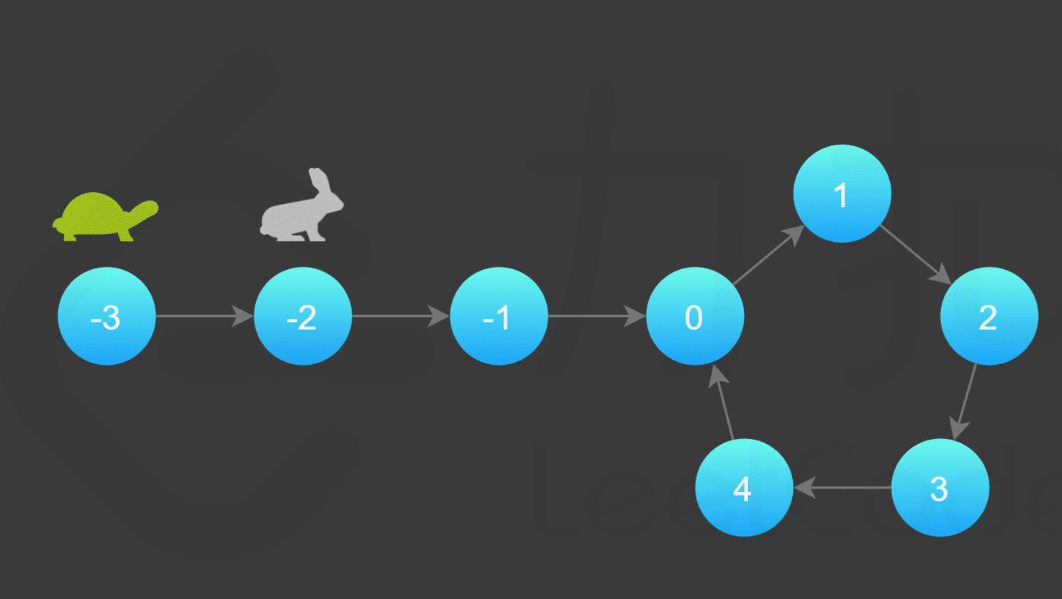
如下图所示，设链表中环外部分的长度为 a 。
- slow 指针进入环后，又走了 b 的距离与 fast 相遇。
- 此时，fast 指针已经走完了环的 n 圈，因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc=a+(n+1)b+nc。
- 根据题意，任意时刻，fast 指针走过的距离都为 slow 指针的 2 倍。
- 因此，我们有
a+(n+1)b+nc=2(a+b) ⟹ a=c+(n−1)(b+c)- 有了
a=c+(n−1)(b+c)的等量关系，我们会发现：从相遇点到入环点的距离加上 n−1 圈的环长，恰好等于从链表头部到入环点的距离。
- 因此，当发现 slow t 相遇时，我们再额外使用一个指针 ptr 。
- 起始，它指向链表头部；随后，它和 slow 每次向后移动一个位置。
- 最终，它们会在入环点相遇。
代码：
var detectCycle = function(head) {
if (head === null) {
return null;
}
let slow = head, fast = head;
while (fast !== null) {
slow = slow.next; // 慢指针移动一个
if (fast.next !== null) {
fast = fast.next.next; // 快指针移动两个
} else {
return null; // 链表无环
}
if (fast === slow) {
let ptr = head;
//当 slow 与 fast 相遇时，指针 ptr。指向链表头部；随后，它和 slow 每次向后移动一个位置。最终，它们会在入环点相遇。
while (ptr !== slow) {
ptr = ptr.next;
slow = slow.next;
}
return ptr;
}
}
return null;
};
相交链表
题目：（题目来源 leetcode)
- 给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。
- 如果两个链表不存在相交节点，返回 null 。
- 图示两个链表在节点 c1 开始相交：
题目数据 保证 整个链式结构中不存在环。
注意，函数返回结果后，链表必须 保持其原始结构
哈希表法
思路：
判断两个链表是否相交，可以使用哈希集合存储链表节点。
首先遍历链表 headA，并将链表 headA 中的每个节点加入哈希集合中。
然后遍历链表 headB，对于遍历到的每个节点，判断该节点是否在哈希集合中：
- 如果当前节点不在哈希集合中，则继续遍历下一个节点；
*如果当前节点在哈希集合中，则后面的节点都在哈希集合中，即从当前节点开始的所有节点都在两个链表的相交部分，因此在链表 headB 中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点，返回该节点。
如果链表 headB 中的所有节点都不在哈希集合中，则两个链表不相交，返回 null。
时间复杂度：O(m+n)，其中 m 和 n 是分别是链表 headA 和 headB 的长度。需要遍历两个链表各一次。
空间复杂度：O(m)，其中 m 是链表 headA 的长度。需要使用哈希集合存储链表 headA 中的全部节点。
代码：
var getIntersectionNode = function(headA, headB) { const visited = new Set(); let temp = headA; while (temp !== null) { visited.add(temp); temp = temp.next; } temp = headB; while (temp !== null) { if (visited.has(temp)) { return temp; } temp = temp.next; } return null; };
双指针法
链表中快慢指针有两种形式：
- 移动位置大小不一样的快慢指针：快慢指针起始位置相同，移动的距离不同。
- 移动起始距离不一样的快慢指针：快慢指针起始位置不同，移动的距离相同。
思想：
- 使用双指针的方法，可以将空间复杂度降至 O(1)。
- 只有当链表 headA 和 headB 都不为空时，两个链表才可能相交。
- 首先判断链表 headA 和 headB 是否为空，如果其中至少有一个链表为空，则两个链表一定不相交，返回 null。
- 当链表 headA和 headB 都不为空时，创建两个指针 pA 和 pB，初始时分别指向两个链表的头节点 headA 和 headB，然后将两个指针依次遍历两个链表的每个节点。具体做法如下：
- 每步操作需要同时更新指针 pA 和 pB。
- 如果指针 pA 不为空，则将指针 pA 移到下一个节点；
- 如果指针 pB 不为空，则将指针 pB 移到下一个节点。
- 如果指针 pA 为空，则将指针 pA 移到链表 headB 的头节点；
- 如果指针 pB 为空，则将指针 pB 移到链表 headA 的头节点。
- 当指针 pA和 pB 指向同一个节点或者都为空时，返回它们指向的节点或者 null。
- 时间复杂度：O(m+n)，其中 m 和 n是分别是链表 headA 和 headB 的长度。两个指针同时遍历两个链表，每个指针遍历两个链表各一次。
- 空间复杂度：O(1)。
- (核心思想是将两个链表用两个指针都遍历一遍，那么当遍历到相同长度时，两个指针一定会相遇，第一次相遇时即为相交节点)
代码：
var getIntersectionNode = function(headA, headB) { if (headA === null || headB === null) { return null; } let pA = headA, pB = headB; while (pA !== pB) { pA = pA === null ? headB : pA.next; pB = pB === null ? headA : pB.next; } return pA; };
链表双指针法
起点不一致的快慢指针
起点不一致的快慢指针：指的是两个指针从同一侧开始遍历链表，但是两个指针的起点不一样。 快指针
fast比慢指针slow先走n步，直到快指针移动到链表尾端时为止。
起点不一致的快慢指针求解步骤
- 使用两个指针
slow、fast：slow、fast都指向链表的头节点，即：slow = head，fast = head。
- 先将快指针向右移动
n步。然后再同时向右移动快、慢指针。 - 等到快指针移动到链表尾部（即
fast == null）时跳出循环体。
起点不一致的快慢指针伪代码模板
// 链表节点的定义
class ListNode {
constructor(val, next = null) {
this.val = (val === undefined ? 0 : val);
this.next = next;
}
}
// 假设我们有一个链表 head，以及一个整数 n
// 这里我们不会实际创建链表，但会假设它存在
// let head = new ListNode(1, ...); // 根据需要添加节点
// let n = ...; // 给定一个正整数
// `slow`、`fast` 都指向链表的头节点
function findMiddleNode(head, n) {
let slow = head;
let fast = head;
// 先让 fast 向前走 n 步
while (n > 0 && fast !== null) {
fast = fast.next;
n--;
}
// 如果 fast 已经为 null，说明链表长度小于 n，直接返回 null 或 head（如果 n 大于链表长度的一半）
if (fast === null) {
return n % 2 === 0 ? head : null; // 根据需要调整，这里假设返回头节点如果 n 恰好是长度的一半
}
// 同时移动 slow 和 fast，直到 fast 到达链表末尾
while (fast !== null && fast.next !== null) {
fast = fast.next.next;
slow = slow.next;
}
// 此时 slow 指向了链表的中点（或接近中点的节点，如果链表长度为奇数）
return slow;
}
// 使用示例（假设链表和 n 已经定义）
// let middleNode = findMiddleNode(head, n);
// console.log(middleNode);
起点不一致的快慢指针适用范围
起点不一致的快慢指针主要用于找到链表中倒数第 k 个节点、删除链表倒数第 N 个节点等。
删除链表的倒数第 N 个结点
题目：
给你一个链表，删除链表的倒数第
n个结点，并且返回链表的头结点。
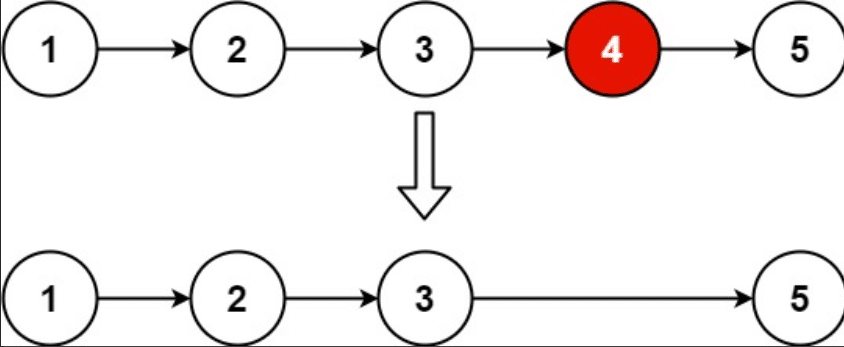
示例：
输入：head = [1,2,3,4,5], n = 2 输出：[1,2,3,5]输入：head = [1], n = 1 输出：[]输入：head = [1,2], n = 1 输出：[1]提示：
链表中结点的数目为 sz 1 <= sz <= 30 0 <= Node.val <= 100 1 <= n <= sz
- 进阶：你能尝试使用一趟扫描实现吗？
方法一：双指针法
思路：
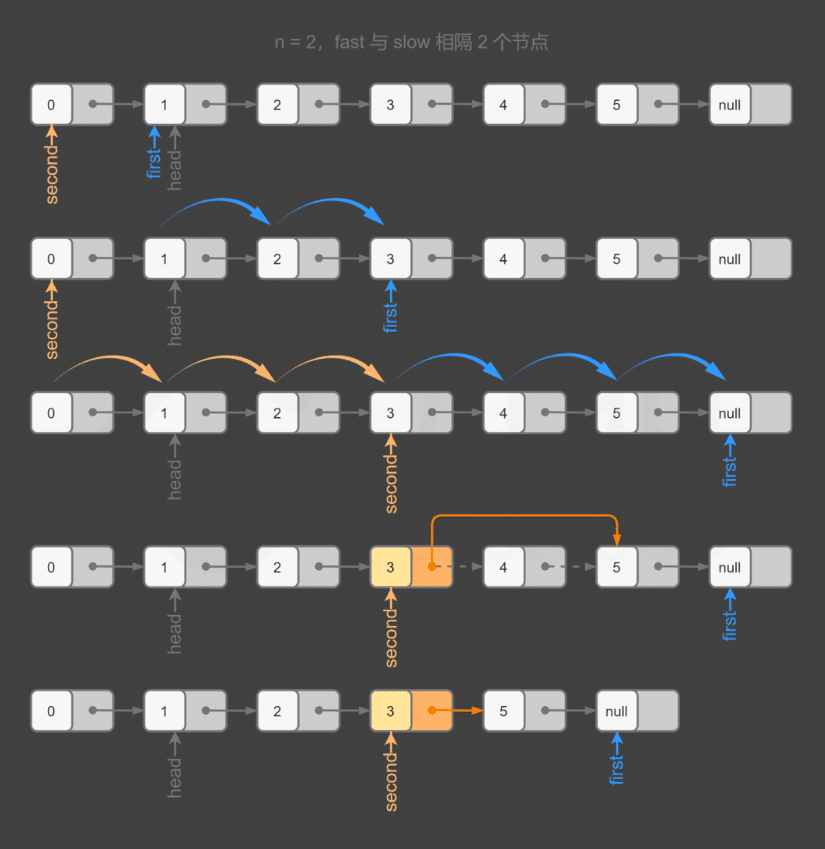
由于我们需要找到倒数第 n 个节点，因此我们可以使用两个指针 fast 和 slow 同时对链表进行遍历，并且 fast 超前 n 个节点。
当 fast 遍历到链表的末尾时，slow 就恰好处于倒数第 n 个节点。
由于删除链表的节点需要找到链表的前驱节点，因此需要遍历到倒数 n+1 个节点；
为了避免单独判断头节点的特殊情况，同样可以在链表头添加哑节点，并将 slow 指针指向哑节点，fast 指向头节点，那么当 fast 移动到链表末尾时，slow 刚好指向被删除节点的前驱节点。
代码：
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} n
* @return {ListNode}
*/
var removeNthFromEnd = function(head, n) {
// 创建哑节点，哑节点指向头部节点
let dummy = new ListNode(null,head);
let slow = dummy; // slow 节点指向哑节点
let fast = head;
while(n>0) { // fast 前进 n 个节点
fast = fast.next;
n--;
}
while(fast) { // 同时移动 slow 和 fast,直到 fast 指向链表尾部，此时 slow 刚好指向被删除节点的前驱节点
fast = fast.next;
slow = slow.next;
}
slow.next = slow.next.next;// 删除节点
return dummy.next; //返回 head 节点
};
方法二：计算链表长度
首先从头节点开始对链表进行一次遍历，得到链表的长度 L。
随后我们再从头节点开始对链表进行一次遍历，当遍历到第
L−n+1个节点时，它就是我们需要删除的节点。
- 为了与题目中的 n 保持一致，节点的编号从 1 开始，头节点为编号 1 的节点。
为了方便删除操作，我们可以从哑节点开始遍历
L−n+1个节点。当遍历到第L−n+1个节点时，它的下一个节点就是我们需要删除的节点，这样我们只需要修改一次指针，就能完成删除操作。
时间复杂度：O(L)，其中 L 是链表的长度。
空间复杂度：O(1)。
注意：
- 如果我们要删除节点 y，我们需要知道节点 y 的前驱节点 x，并将x 的指针指向y 的后继节点。
- 但由于头节点不存在前驱节点，因此我们需要在删除头节点时进行特殊判断。
- 但如果我们添加了哑节点（哑节点（dummy node），它的 next 指针指向链表的头节点），那么头节点的前驱节点就是哑节点本身，此时我们就只需要考虑通用的情况即可。
代码：
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} n
* @return {ListNode}
*/
var removeNthFromEnd = function(head, n) {
let len = 0;
let curNode = head;
while(curNode) {
++ len ;
curNode = curNode.next;
}
// 注意：创建哑节点，链接头节点，用于避免头节点的判断
let dummy = new ListNode(null,head);
curNode = dummy; // 从哑节点处开始遍历
for(let i = 1; i < len-n+1; ++i) {
curNode = curNode.next;
}
curNode.next = curNode.next.next;
return dummy.next;
};
方法三：栈
思路：
- 遍历链表，并将每个节点入栈；
- 遍历完成后，依次弹出栈顶元素，弹出的第 n 个元素即为要删除的节点，第
n+1个元素即为被删除节点的前驱节点；- 注意：由于删除头节点需要特殊判断，因此同样可以在链表头部添加哑节点，避免头节点的特殊判断；
- 时间复杂度 O(n)，空间复杂度 O(n)，n 为链表长度；
代码：
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} n
* @return {ListNode}
*/
var removeNthFromEnd = function(head, n) {
let stack = [];
let dummy = new ListNode(null,head);//创建 dummy,用于避免删除头节点的特殊判断
let curNode = dummy;//从 dummy 节点开始入栈，考虑删除头节点情况
while(curNode) {
stack.push(curNode);
curNode = curNode.next
}
while(n>0) { // 出栈，直到节点 n
stack.pop()
n--;
}
curNode = stack.pop(); // 获取被删除节点的前驱节点
curNode.next = curNode.next.next; // 删除节点
return dummy.next; // 返回 dummy 节点的后继节点！
};
步长不一致的快慢指针
步长不一致的快慢指针：指的是两个指针从同一侧开始遍历链表，两个指针的起点一样，但是步长不一致。
例如，慢指针
slow每次走1步，快指针fast每次走两步。直到快指针移动到链表尾端时为止。
步长不一致的快慢指针求解步骤
- 使用两个指针
slow、fast。slow、fast都指向链表的头节点。 - 在循环体中将快、慢指针同时向右移动，但是快、慢指针的移动步长不一致。比如将慢指针每次移动
1步，即slow = slow.next。快指针每次移动2步，即fast = fast.next.next。 - 等到快指针移动到链表尾部（即
fast == None）时跳出循环体。
步长不一致的快慢指针伪代码模板
fast = head
slow = head
while( fast && fast.next) {
slow = slow.next
fast = fast.next.next
}
步长不一致的快慢指针适用范围
步长不一致的快慢指针适合寻找链表的中点、判断和检测链表是否有环、找到两个链表的交点等问题。
链表的中间结点
题目：
描述：给定一个单链表的头节点
head。要求：返回链表的中间节点。如果有两个中间节点，则返回第二个中间节点。
说明：
- 给定链表的结点数介于
1和100之间。示例：
输入：[1,2,3,4,5] 输出：此列表中的结点 3 (序列化形式：[3,4,5]) 解释：返回的结点值为 3 。 注意，我们返回了一个 ListNode 类型的对象 ans，这样： ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL. 输入：[1,2,3,4,5,6] 输出：此列表中的结点 4 (序列化形式：[4,5,6]) 解释：由于该列表有两个中间结点，值分别为 3 和 4，我们返回第二个结点。
方法一：单指针
先遍历一遍链表，统计一下节点个数为 n，再遍历到 n / 2 的位置，返回中间节点。
// 假设 ListNode 类已经定义
// class ListNode {
// constructor(val, next = null) {
// this.val = (val === undefined ? 0 : val);
// this.next = next;
// }
// }
function middleNode(head) {
let n = 0;
let curr = head;
// 计算链表长度
while (curr) {
n++;
curr = curr.next;
}
// 初始化 curr 为头节点，并计算中间节点的索引
curr = head;
let k = 0;
// 移动到中间节点
while (k < Math.floor(n / 2)) {
k++;
curr = curr.next;
}
// 返回中间节点
return curr;
}
// 使用示例（假设链表 head 已经定义）
// let head = new ListNode(1, ...); // 根据需要添加节点
// let middle = middleNode(head);
// console.log(middle); // 输出中间节点的值或进行其他操作
复杂度分析
- 时间复杂度：O(n)。
- 空间复杂度：O(1)
方法二：快慢指针
使用步长不一致的快慢指针进行一次遍历找到链表的中间节点。具体做法如下：
- 使用两个指针
slow、fast。slow、fast都指向链表的头节点。 - 在循环体中将快、慢指针同时向右移动。
- 其中慢指针每次移动
1步，即slow = slow.next。 - 快指针每次移动
2步，即fast = fast.next.next。
- 其中慢指针每次移动
- 等到快指针移动到链表尾部（即
fast == null）时跳出循环体，此时slow指向链表中间位置。 - 返回
slow指针。
// 假设 ListNode 类已经定义
// class ListNode {
// constructor(val, next = null) {
// this.val = (val === undefined ? 0 : val);
// this.next = next;
// }
// }
function middleNode(head) {
let fast = head;
let slow = head;
// 当 fast 和 fast.next 都存在时，循环继续
while (fast && fast.next) {
slow = slow.next; // 慢指针每次移动一步
fast = fast.next.next; // 快指针每次移动两步
}
// 当循环结束时，slow 指向了中间节点（或当链表长度为奇数时，指向了中间两个节点中靠前的一个）
return slow;
}
// 使用示例（假设链表 head 已经定义）
// let head = new ListNode(1, ...); // 根据需要添加节点
// let middle = middleNode(head);
// console.log(middle.val); // 输出中间节点的值
分离双指针
分离双指针：两个指针分别属于不同的链表，两个指针分别在两个链表中移动。
分离双指针求解步骤
- 使用两个指针
left_1、left_2。left_1指向第一个链表头节点，即：left_1 = list1，left_2指向第二个链表头节点，即：left_2 = list2。 - 当满足一定条件时，两个指针同时右移，即
left_1 = left_1.next、left_2 = left_2.next。 - 当满足另外一定条件时，将
left_1指针右移，即left_1 = left_1.next。 - 当满足其他一定条件时，将
left_2指针右移，即left_2 = left_2.next。 - 当其中一个链表遍历完时或者满足其他特殊条件时跳出循环体。
分离双指针伪代码模板
left_1 = list1
left_2 = list2
while(left_1 && left_2) {
if (条件 1) {
left_1 = left_1.next
left_2 = left_2.next
}else if(条件 2) {
left_1 = left_1.next
}else if(条件 2\3) {
left_2 = left_2.next
}
}
分离双指针适用范围
分离双指针一般用于有序链表合并等问题。
算法题
链表题
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 0707 | 设计链表 | 设计、链表 | 中等 |
| 0083 | 删除排序链表中的重复元素 | 链表 | 简单 |
| 0082 | 删除排序链表中的重复元素 II | 链表、双指针 | 中等 |
| 0206 | 反转链表 | 递归、链表 | 简单 |
| 0092 | 反转链表 II | 链表 | 中等 |
| 0025 | K 个一组翻转链表 | 递归、链表 | 困难 |
| 0203 | 移除链表元素 | 递归、链表 | 简单 |
| 0328 | 奇偶链表 | 链表 | 中等 |
| 0234 | 回文链表 | 栈、递归、链表、双指针 | 简单 |
| 0430 | 扁平化多级双向链表 | 深度优先搜索、链表、双向链表 | 中等 |
| 0138 | 复制带随机指针的链表 | 哈希表、链表 | 中等 |
| 0061 | 旋转链表 | 链表、双指针 | 中等 |
链表双指针题目
| 题号 | 标题 | 标签 | 难度 |
|---|---|---|---|
| 0141 | 环形链表 | 哈希表、链表、双指针 | 简单 |
| 0142 | 环形链表 II | 哈希表、链表、双指针 | 中等 |
| 0160 | 相交链表 | 哈希表、链表、双指针 | 简单 |
| 0019 | 删除链表的倒数第 N 个结点 | 链表、双指针 | 中等 |
| 0876 | 链表的中间结点 | 链表、双指针 | 简单 |
| 剑指 Offer 22 | 链表中倒数第k个节点 | 链表、双指针 | 简单 |
| 0143 | 重排链表 | 栈、递归、链表、双指针 | 中等 |
| 0002 | 两数相加 | 递归、链表、数学 | 中等 |
| 0445 | 两数相加 II | 栈、链表、数学 | 中等 |